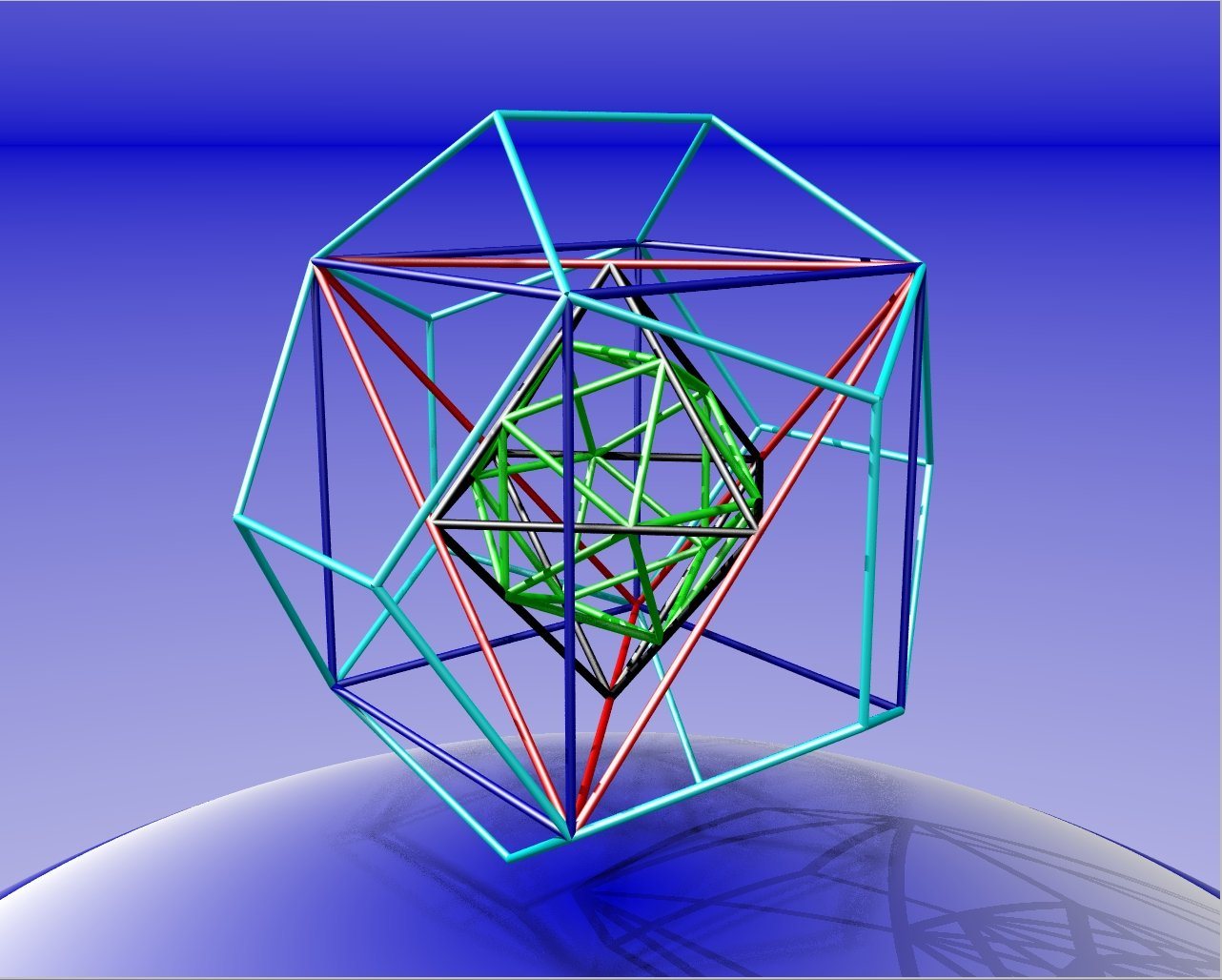
The icosahedron (green) is nested inside the octahedron (grey), its 12 vertices
at the midpoints of the 12 edges of the latter. The octahedron is nested inside the tetrahedron (red), its
six vertices at the midpoints of the six edges of the latter. The tetrahedron is nested inside the cube
(blue), its four vertices coinciding with four vertices of the latter. The cube is nested inside
the dodecahedron (turquoise), its eight corners coinciding with eight
of the 20 vertices of the latter.
An animated gif showing the five nested Platonic solids rotating inside a
circumscribing sphere can be seen at Link

