| << Previous 1... 15 16 17 18 [19] Next >> |
The Tree of Life nature of the five Platonic solids
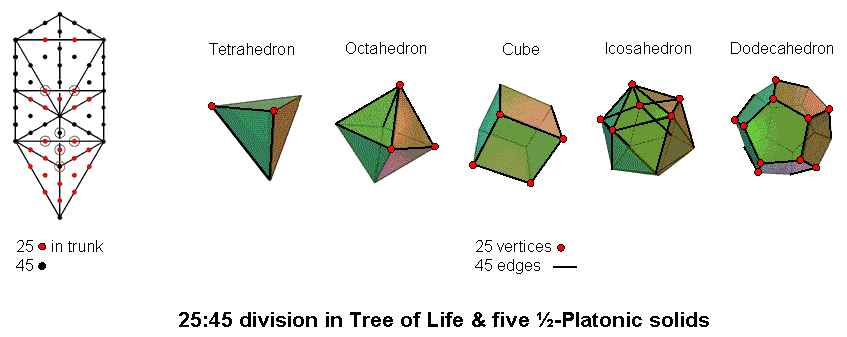
The five Platonic solids have 50 vertices and 90 edges, i.e., their faces are defined by 140 points & straight lines. The number 140 is the number value of Masloth, the Mundane Chakra of Chokmah (also the number value of Malachim, the Order of Angels assigned to Tiphareth). 70 points & lines make up each half of the five Platonic solids. The number 70 is a parameter of holistic systems, being, for example, the number of yods in the outer Tree of Life (see here), the number of corners of the (7+7) enfolded polygons in its inner form (see here), the number of yods that surround the centre of a tetrahedron constructed from tetractyses (see here) and the number of corners of the 43 triangles in the 2-dimensional Sri Yantra (see here). The display of this parameter in the five Platonic solids is one of many indications discussed in this website that they constitute sacred geometry. The table below lists the numbers of vertices & edges in half of each regular polyhedron:
| Platonic solid | Vertices |
Edges |
| Tetrahedron | 2 | 3 |
| Octahedron | 3 | 6 |
| Cube | 4 | 6 |
| Icosahedron | 6 | 15 |
| Subtotal | 15 | 30 |
| Dodecahedron | 10 | 15 |
| Total | 25 | 45 |
The trunk of the Tree of Life consists of the mathematical sequence:
It is symbolized by the four rows of the Pythagorean tetractys (see here). Constructed from tetractyses, there are 25 hexagonal yods in the trunk (two in the "line," seven in the "triangle" & 16 in the "tetrahedron"), so that the rest of the Tree outside its trunk (what may be called its "branches") has (70−25=45) yods (10 corners & 35 hexagonal yods). Comparing this with the numbers of vertices and edges indicated by the table to be in the five halves of the Platonic solids, we see that their 25 vertices correspond to the 25 red hexagonal yods in the trunk and the 45 edges correspond to the 45 black yods in the branches of the Tree of Life:

Intuitively, this feels correct because the trunk of any tree is its core (the
geometrical sequence symbolizing the numbers 1, 2, 3 & 4 is the counterpart of this in the Tree of
Life), and the 25 vertices marking out the five halves of the Platonic solids can certainly be regarded
as their core in the sense that these points are the basic geometrical elements needed to construct
them. 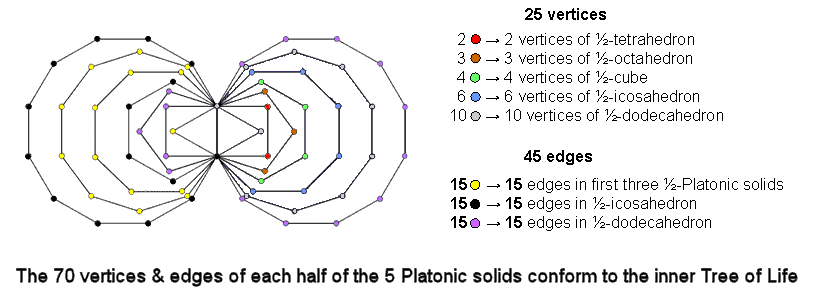
In the case of the 70 corners of the (7+7) enfolded polygons of the inner Tree of Life, there are 35 corners associated with each set of seven polygons. Ten corners outside their shared root edge belong to each dodecagon. The counterparts in the inner Tree of Life of the 25 vertices and 45 edges of the five half-Platonic solids are, therefore, the 25 corners associated with one set of the first six enfolded polygons (which constitute another holistic set of polygons) and the (10+35=45) corners associated with the eight other polygons. The set of 25 corners comprises the 15 corners associated with the square (2), pentagon (3), hexagon (4) & octagon (6) and the 10 corners associated with the triangle (2) & decagon (8). This compares with the 15 vertices of the halves of the first four solids: tetrahedron (2), octahedron (3), cube (4) & icosahedron (6) and the 10 vertices of the half-dodecahedron. Notice that the numbers of corners of the polygons are the same as the numbers of the vertices. The set of 45 corners comprises the 15 corners associated with the hexagon (5) & dodecagon (10) and the 30 corners associated with the triangle, square, pentagon, octagon, decagon & the other dodecagon. This compares with the 15 edges in half a dodecahedron and the 30 edges in the halves of the first four Platonic solids. The 70 vertices & edges in the halves of all five Platonic solids correspond to the 70 corners of the 14 enfolded polygons making up the inner Tree of Life. The Godname YAH of Chokmah with number value 15 prescribes the first four half-Platonic solids because they have 15 vertices that are symbolized in the diagram opposite by the 15 corners of the first five enfolded polygons on the right-hand side. They also have 30 edges, where 30 is the 15th even integer.
| << Previous 1... 15 16 17 18 [19] Next >> |