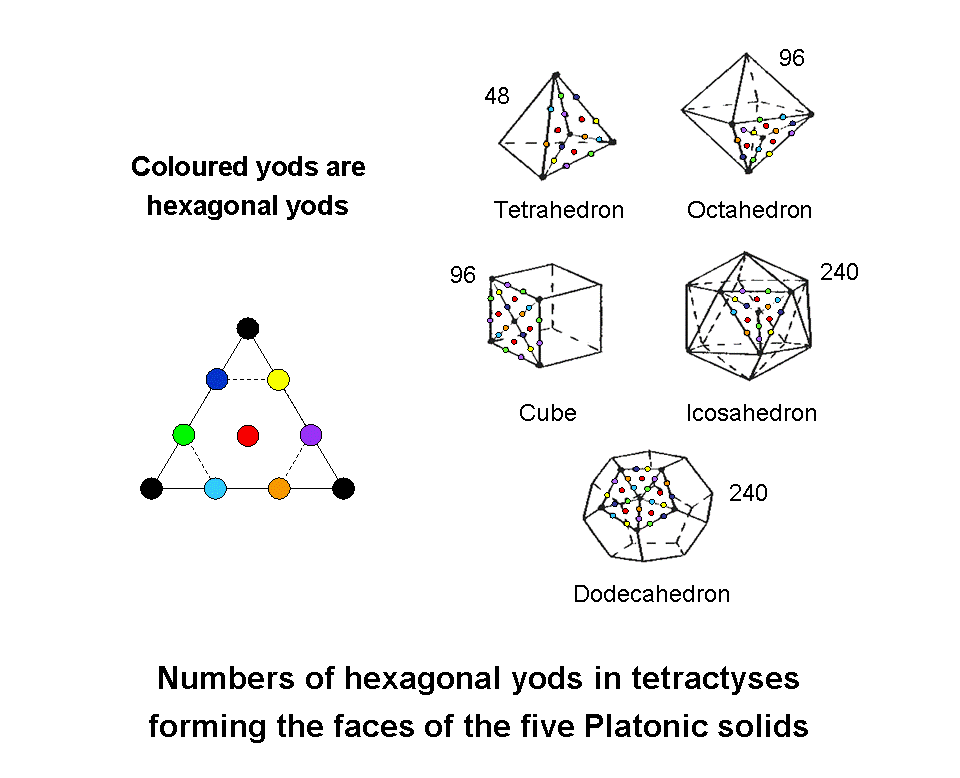
The same number 240 is embodied in the Platonic solids as the 240 hexagonal yods in the faces of the tetrahedron, octahedron & cube and as the 240 hexagonal yods in the faces of the icosahedron or dodecahedron when their faces are constructed from the template of the tetractys by transforming their sectors into the latter. This 240:240 division of hexagonal yods making up the first four Platonic solids is the regular polyhedral manifestation of a fundamental pattern displayed by holistic systems that corresponds to the 240 roots of each group E₈ in E₈×E₈, one of the two symmetry groups describing the unified force between superstrings. It is the potent Pythagorean tetractys that makes this connection between sacred geometry and the group mathematics that  underlies superstrings. The 480 hexagonal yods in the faces of the first four Platonic solids denote the 480 roots of E₈×E₈. The 240 hexagonal yods in one half of them correspond to the 240 non-zero roots in one group E₈ and the 240 hexagonal yods in their other halves correspond to the 240 non-zero roots in the second, similar group. The tetrahedron has 24 hexagonal yods in two of its four faces and the octahedron (or cube) has 48 hexagonal yods in half its faces. There are (24+48=72) hexagonal yods in half their faces, leaving 168 hexagonal yods. This 72:168 division is the counterpart of the 720:1680 division encountered on page 1 in the disdyakis triacontahedron when 720 geometrical elements are added to the 1680 geometrical elements surrounding its axis when its 120 faces are each divided into three sectors. The division is characteristic of all holistic systems (see The holistic pattern). It corresponds to the division of the 240 non-zero roots of E₈ into the 72 roots of its exceptional subgroup E₆ and 168 other roots (see the second picture on #13 of Superstrings as sacred geometry/Tree of Life).

  

<< Previous    1...   2  3  [4]  5  6  ...18    Next >>

Home