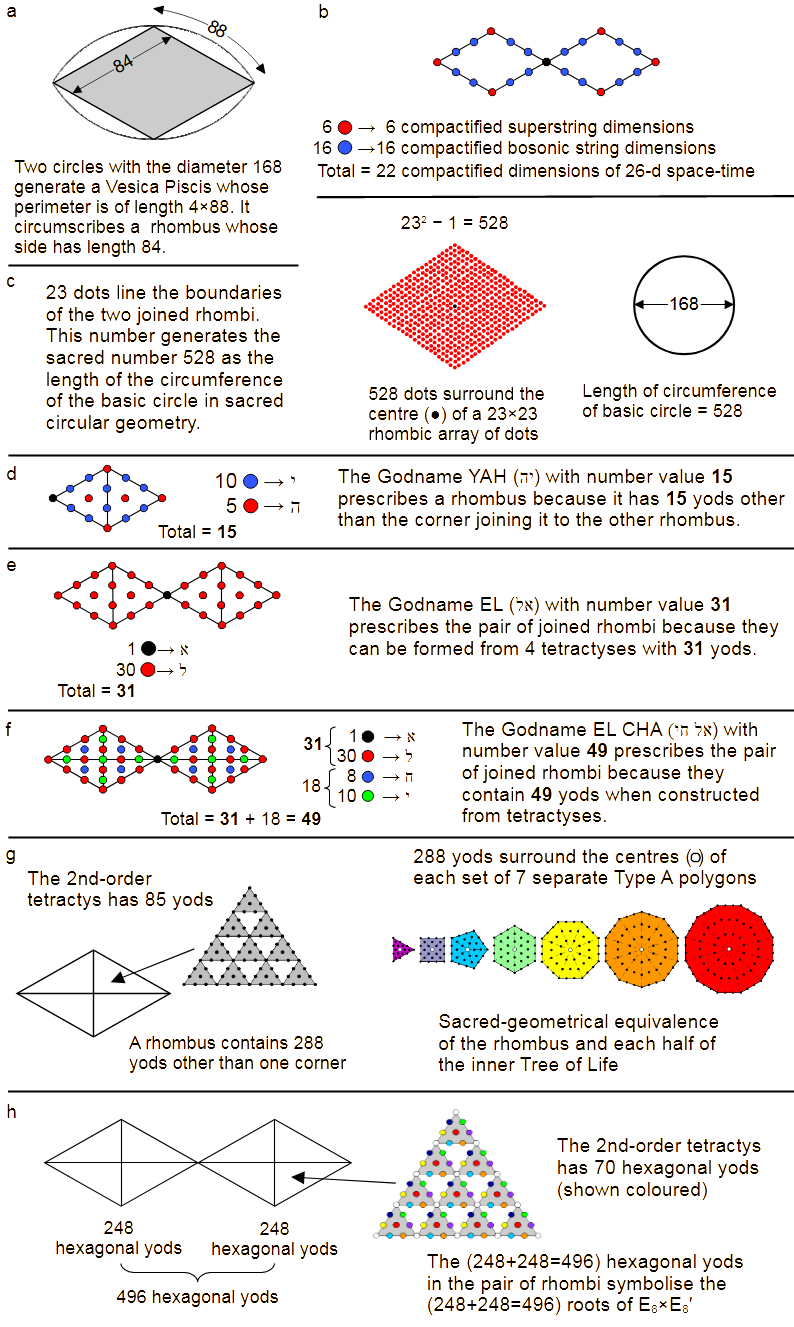
a

 

b

c

d

e

f

g

h

In order for straight-line and circular sacred geometries to be isomorphic to one another, all of the smallest similar circles in the latter have to be given the specific diameter of 168 units. Two such circles overlapping centre-to-circumference generate the Vesica Piscis, consisting of four of the six arcs that make up each circle. Every arc is 88 units long and the chord joining its ends is 84 units long, being a side of the hexagon whose corners mark out the ends of the six arcs making up the circle.
Transformation of polygons by turning their sectors into tetractyses, Type A triangles, etc., leaves four yods spaced evenly along their sides. Two such transformed rhombi have 23 yods lining their eight sides. The 22 yods surrounding the corner joining them consist of 6 red corners and 16 blue hexagonal yods. This 6:16 division in the numbers of the two types of yods lining the sides of the two rhombi manifests in bosonic string theory. They obey the laws of quantum mechanics provided that they exist in a space-time that is 26-dimensional. As superstrings require space-time to have 10 dimensions, four of which define the 4-d Minkowski space-time of the large-scale universe, this means that six of their dimensions must extend only on a microscopic scale, i.e., they are "compactified." So, too, must be the remaining 16 dimensions associated with bosonic strings. The 22 compactified dimensions consist of two types: six superstring and 16 bosonic string. That the same division arises as with the yods on the boundary of two rhombi should come as no surprise because, if the latter truly constitute "sacred geometry" that contains the blueprint for matter, its patterns should re-appear in the discoveries of theoretical physics.
If, next, we consider a rhombus with 23 dots spaced evenly along each side, there are 88 dots on its boundary (84 other than its four corners). This is analogous to the fact that every one of the six arcs of length 88 making up a circle of diameter 168 is four units longer than its associated chord. In a 23×23 rhombic array of (23²=529) dots, there are 528 dots surrounding its centre. The sacred number 528 re-appears! Arithmetically speaking there is no mystery to this, for 23² − 1 = (23−1)(23+1) = 22×24 = 22×24×7/7 = (22/7)×168, which is the length of the circumference of a circle of diameter 168.
The Godnames prescribe through their gematria number values the properties of sacred geometry as the archetypal blueprint. We should therefore expect their numbers to appear in the properties of the two rhombi, if they constitute sacred geometry. When the two joined rhombi are each constructed from two tetractyses, there are 15 yods in each one on either side of their connecting yod (coloured black). This is the number value of YAH, the Godname of Chokmah. They comprise 10 blue hexagonal yods on the sides of the tetractyses and five red yods at either their corners or centres. The gematria number value of the Hebrew letter yud (י) is 10 and the number value of the letter heh (ה)  is 5.
Constructed from tetractyses, the two joined rhombi contain 31 yods. This is the number value of EL (אל), the Godname associated with Chesed. The value 1 of alef denotes the black yod shared by the rhombi. The letter value 40 of lamed denotes the 30 yods surrounding it.
Constructed from four tetractyses, each rhombus contains 25 yods. They comprise the same 16 yods that were considered in case e and nine more yods consisting of four blue hexagonal yods at the centres of tetractyses and five green hexagonal yods either lining sides or at the centre of the rhombus. Hence, there are the same 31 yods found in case e but eight more blue hexagonal yods and 10 green hexagonal yods, a total of 49 yods. The number of EL CHAI, the Godname of Yesod, has the number 49. EL has the number value 31, the letter het has the number 8 and the letter yud has the value 10.
The 2nd-order tetractys contains 85 yods. Each side has 13 yods. When each sector of a rhombus is turned into a 2nd-order tetractys, there are (85−13=72) yods per sector, so that (4×72=288) yods surround its centre. This means that each rhombus has 288 yods other than the corner shared with the other one. Compare this with the two sets of polygons of the inner Tree of Life. When Type A and separate, the polygons in each set have 288 yods surrounding their centres. The proof of this is as follows: the number of yods in a Type A polygon with n corners = 6n + 1, there being six yods per sector and "1" denoting its centre. The number of yods surrounding the centres of the seven polygons with 48 corners = ∑ 6n = 6×48 = 288. Each rhombus therefore is made up of the same number of yods as each half of the inner Tree of Life. In terms of CTOL, they symbolise the 288 SLs between the lowest and highest Trees of the 49-tree mapping the cosmic physical plane. The Pythagorean integers 1, 2, 3 & 4 express this number as follows:
                                                                                                               288 = 1!×2!×3!×4!
This is the number of ways 10 objects can form a tetractys pattern by rearranging their order within each of its four rows. These integers also express the number 576 (the number of yods in both rhombi surrounding their shared corner because 576 = 24² = 1²×2²×3²×4².
The 2nd-order tetractys has 85 yods, of which 15 are corners of its 10 1st-order tetractyses, leaving 70 hexagonal yods. Along each side are eight hexagonal yods. When each sector of a rhombus is a 2nd-order tetractys, there are (70−8=62) hexagonal yods per sector, so that each rhombus contains (4×62=248) hexagonal yods. The pair of rhombi contain 496 hexagonal yods. Compare these properties with the symmetry group E₈×E₈' describing the unified forces between one of the two types of heterotic superstrings. The dimension of the rank-8 Lie group E₈ is 248, so that the dimension of E₈×E₈' = 2×248 = 496. The dimension of a Lie group is the number of its so-called "roots." Each yod in one rhombus symbolises a root of E₈; each yod in the other rhombus symbolises a root of E₈', the direct product E₈×E₈' arising because the two rhombi are similar. The other type of heterotic superstring has the symmetry group SO(32) (the only other non-trivial group with dimension 496). An octagon constructed from 2nd-order tetractyses has (8×62=496) hexagonal yods. We have already seen that each rhombus corresponds to half of the inner Tree of Life. Each rhombus performs the function of a square present in each separate half. In other words, the complete form of both halves of the inner Tree contributes to the population of 496 hexagonal yods, whereas only one half is required if a single octagon (rather than two squares) should be regarded as the representation of the 496 roots required of a superstring gauge symmetry group that, as originally proved by physicists Michael Green & John Schwarz, for it to apply to a quantum field theory that is free of quantum anomalies. The analogy established here between the two rhombi and the two halves of the inner Tree of Life argues against SO(32) being compatible with this representation of the cosmic blueprint.