|
|
|
|
Coxeter plane projection of the 421 polytope. It has 6720 edges. |
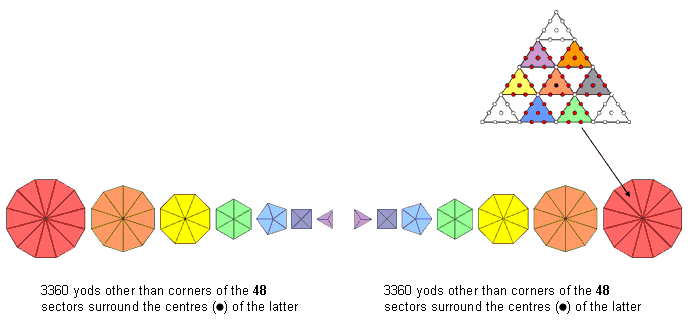
6720 yods other than their corners surround the centres of the 48 sectors of the (7+7) separate polygons when they are 2nd-order tetractyses. |
|
|
|
| << Previous 1... 19 20 [21] 22 23 ...24 Next >> |
21. The 421 polytope as the inner form of the Tree of Life
|
|

|
|
Coxeter plane projection of the 421 polytope. It has 6720 edges. |
6720 yods other than their corners surround the centres of the 48 sectors of the (7+7) separate polygons when they are 2nd-order tetractyses. |
|
|
|
A 2nd-order tetractys has 85 yods. 13 yods line each side, so each sector of an n-gon adds (85−13=72) yods when it is a 2nd-order tetractys. The number of yods in such an n-gon ≡ N(n) = 72n + 1, where "1" denotes its centre. The number of yods surrounding the centres of the n sectors other than their corners = N(n) − (n+1) − n = 70n. The number of yods other than corners of the 48 sectors of the seven separate polygons of the inner Tree of Life that surround their centres = 70×48 = 3360. There are (3360+3360=6720) such yods in the (48+48=96) sectors in the two sets of seven separate polygons. 192 corners & triangles and 192 sides surround their centres. The division: 384 = 192 + 192 in the geometrical composition of the two sets of polygons is characteristic of holistic systems (see here). It corresponds to the division: 6720 = 3360 + 3360 in the yods surrounding the centres of the 96 sectors when they are 2nd-order tetractyses.
The 421 polytope, whose 240 vertices determine the positions in 8-dimensional space of the 240 roots of the rank-8 exceptional Lie group E8, has 6720 edges (3360 edges in each half). They are symbolised in the inner Tree of Life by the 3360 yods other than corners of sectors that surround the centres of the latter in each set of seven separate polygons, one the mirror image of the other.
When the sectors of an n-gon are 1st-order tetractyses, there are 6 yods per sector, of which one is the corner of the n-gon and one is its central hexagonal yod. 4n hexagonal yods surround the centres of the sectors of an n-gon. Each set of seven polygons has (4×48=192) such hexagonal yods, both sets having (192+192=384) such yods. The 192:192 division of the number 384 is characteristic of this parameter of holistic system (see here). Its counterpart when sectors are 2nd-order tetractyses is the 3360:3360 division of the number 6720, which corresponds to the two halves of the 421 polytope. The 48 sectors of the seven separate polygons consist of the 24 sectors of the triangle, square, pentagon & dodecagon and the 24 sectors of the hexagon, octagon & decagon. This 24:24 division is characteristic of holistic systems. When their sectors are 2nd-order tetractyses, each set of polygons with 24 sectors has (70×24=1680) yods other than sector corners surrounding centres of sectors. The 1680:1680 division of the number 3360 is also characteristic of holistic systems (see here). It manifests in the UPA/subquark state of the E8×E8 heterotic superstring as the 1680 turns in an outer or inner half-revolution of its 10 whorls. As each turn is a circularly polarised oscillation, it is a supposition of two orthogonal plane waves with a 90° phase difference. The 3360 yods in one set of polygons (further divided into two sets of 1680) symbolise the 3360 plane waves in an outer half-revolution of the 10 whorls and the 3360 yods in the other set (further divided into two sets of 1680) symbolise the 3360 plane waves in an inner half-revolution of the 10 whorls. The 24:24 division of corners in a set of seven polygons manifests as the 1680 pairs of plane waves in either an outer or inner half-revolution of the 10 whorls.
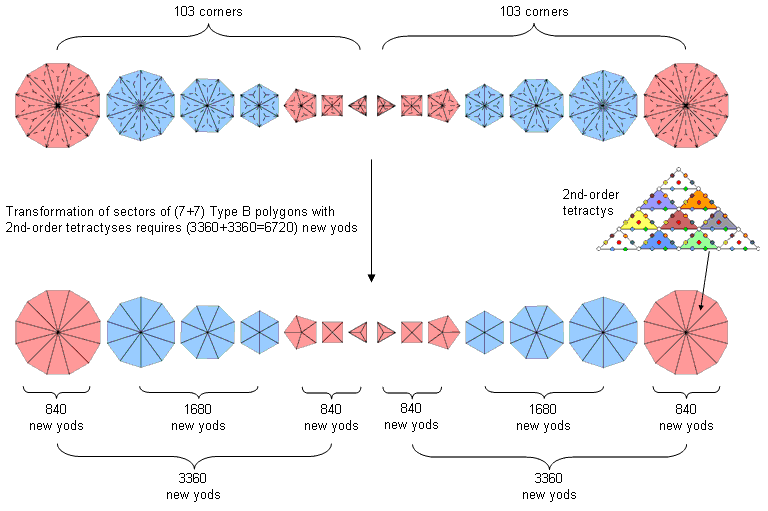
The exclusion of corners of sectors and their centres may be understood as follows. The 48 sectors of the seven Type B polygons have (48+48+7=103) corners. As the centre of each sector becomes the centre of the 2nd-order tetractys when the latter replaces it, the construction of these polygons from 2nd-order tetractyses requires 3360 new yods (1680 new yods in the triangle, square, pentagon & dodecagon and 1680 new yods in the hexagon, octagon & decagon):
|
| Transformation of the (7+7) separate Type A polygons with 2nd-order tetractyses requires (3360+3360=6720) new yods. |
When their sectors are 2nd-order tetractyses, both sets of seven separate Type B polygons need (3360+3360=6720) new yods in addition to their original (103+103=206) corners. Here is a remarkable conjunction of two holistic parameters. The number 206 denotes the 206 bones in the human skeleton (see here) and the number 6720 denotes the number of edges of the 421 polytope, whose vertices represent the roots of the E8 symmetry group governing the interactions of E8×E8 heterotic superstrings. They have analogous functions, for both shape the outer form of holistic systems, namely, the UPA (6720 oscillations of plane waves in one revolution of its 10 whorls) and the human body. Can the reader regard it plausible that this might be no more than coincidence? If he does, he believes in miracles. If he does not, he has to believe in divine design, as embodied in the sacred geometries of some of the world's major religions. There are no alternatives.
The number of corners & sides of the 3n triangles surrounding the centre of a Type B polygon with n sides = 7n. Surrounding the centres of the seven Type B polygons making up the inner Tree of Life are (48×7=336) corners & sides of (48×3=144) triangles. Surrounding the centres of the (7+7) Type B polygons are (336×2=672) corners & sides of (144×2=288) triangles.
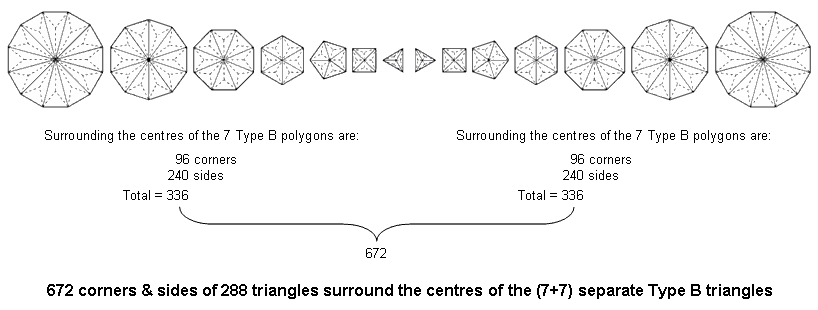
This is the geometrical counterpart of the 672 yods in the first four Platonic solids (see #15), the 672 yods in the 3-d Sri Yantra other than the corners of its 42 triangles (#16) and the 672 corners, sides & triangles surrounding the centres of the two Type C dodecagons (#17).
| << Previous 1... 19 20 [21] 22 23 ...24 Next >> |