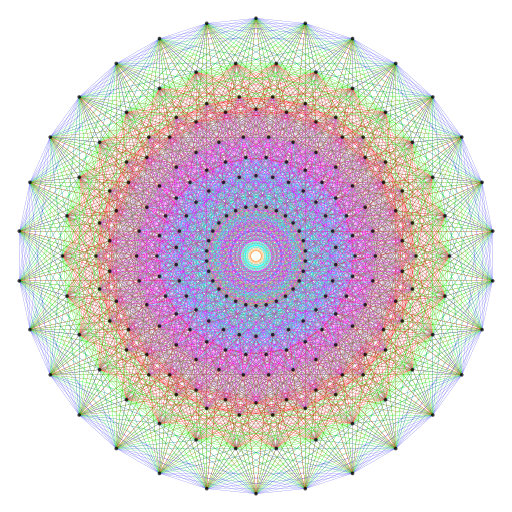
Each half of the 421 polytope has 3360 edges.
| << Previous 1... 17 18 [19] 20 21 ...24 Next >> |
19. The Godname EL CHAI prescribes the number of edges of the 421 polytope
 |
 |
|
Each half of the 421 polytope has 3360 edges. |
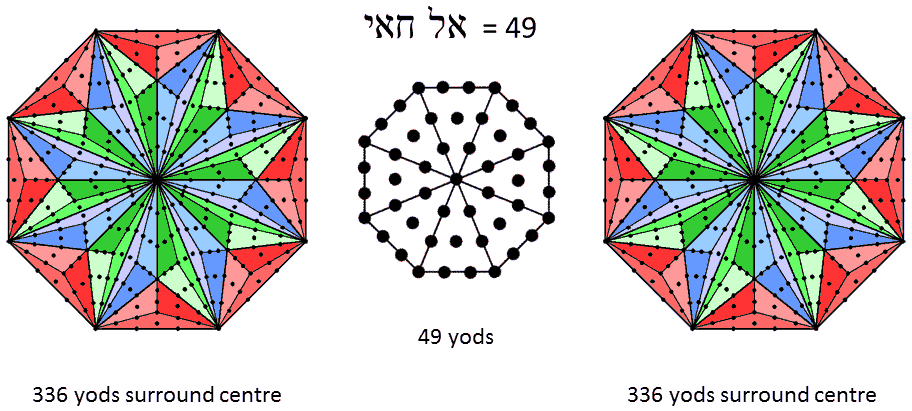
The number value 49 of EL CHAI, the Godname of Yesod, is the number of yods in an octagon with tetractyses as sectors. 336 yods surround the centre of a Type C octagon. Weighted with the Decad, the 672 yods surrounding the centres of the two Type C octagons generate the number (6720) of edges of the 421 polytope. |
An octagon whose sectors are tetractyses contains 49 yods. This is the number value of EL CHAI ("God Almighty"), the Godname of Yesod. The centre of the Type C octagon is surrounded by 336 yods.* Weighted with the number 10 (Decad), the 672 yods surrounding the centres of the two Type C octagons that are part of the inner Tree of Life generate the number 6720. This is the number of edges of the 421 polytope. When they are Type B, the two octagons have 240 yods surrounding their centres.** This is the number of vertices of the 421 polytope. Can it be coincidence that both the number of vertices and the number of edges of the 421 polytope are embodied in consecutive types of octagons? Of course not! Instead, it demonstrates how the Godnames of the Sephiroth constitute powerful, mathematical archetypes that determine through sacred geometry and number the very nature of the divine paradigm that underlies the E8 symmetry of the superstring forces forming the physical universe.
The physical significance of the Decad in this context is that it refers to the 10 whorls of the UPA. The 336 yods surrounding each Type C octagon denote the two sets of 336 plane wave components of the 336 circularly polarised waves in each revolution of a whorl, the weight 10 assigned to them indicating that this oscillatory pattern is repeated in all 10 whorls.
As
152 − 1 = 224,
15×(152 − 1) = 5×3×224 = 5×672 = 3360 = 153 − 15.
This shows how the Godname YAH with number value 15 prescribes the 3360 edges in each half of the 421 polytope. As
3360 = 15×(152 − 1) = 15×(3+5+7+...+29),
6720 = 2×3360 = 30×(3+5+7+....+29) = 10×(9+15+21+...+87).
This shows how the number of edges in the 421 polytope is determined not only by the Godname of Yesod but also by the number value 87 of its Mundane Chakra, Levanah. As 6720 = 84×80, this number is generated by assigning the number 80 of Yesod to the 84 yods surrounding the centre of a 2nd-order tetractys:
 |
|
The number 80 of Yesod determines the number of edges of the 421 polytope as a holistic object represented by the 2nd-order tetractys. |
The Tetrad is symbolised by the four corners of a square. When the 25 yods of a Type A square are weighted with the number 672, they generate the number 16800:
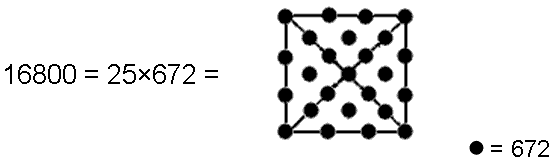 |
| The Tetrad symbolised by the square generates the number of turns in the 10 helical whorls of the UPA/superstring through the number 672 embodied in sacred geometries and in the 421 polytope. |
This is evidence showing the mathematical connection between the superstring structural parameter 16800 paranormally discovered over a century ago, the geometrical symbol of the four Elements of Earth, Water, Air & Fire and the holistic parameter 672 found in sacred geometries and in the 421 polytope.
For more details on how sacred geometries embody properties that are analogous to the vertices & edges of the 421 polytope, see Article 63 (Web, PDF).
* Proof: A Type C polygon with n sides has (42n+1) yods. A Type C octagon (n=8) has 337 yods. 336 yods surround its centre.
** Proof: A Type B polygon with n sides has (15n+1) yods. A Type B octagon has 121 yods. 120 yods surround its centre. (120+120=240) yods surround the centres of two Type B octagons.
| << Previous 1... 17 18 [19] 20 21 ...24 Next >> |