| << Previous 1... 31 32 [33] 34 35 ...39 Next >> |
#33 Properties of the two "halves" of the seven separate/enfolded, Type A polygons
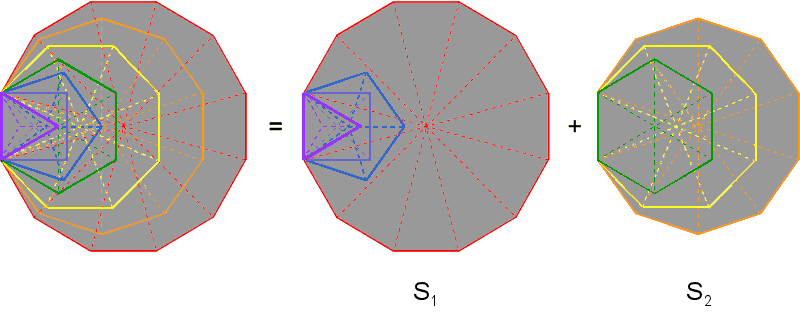
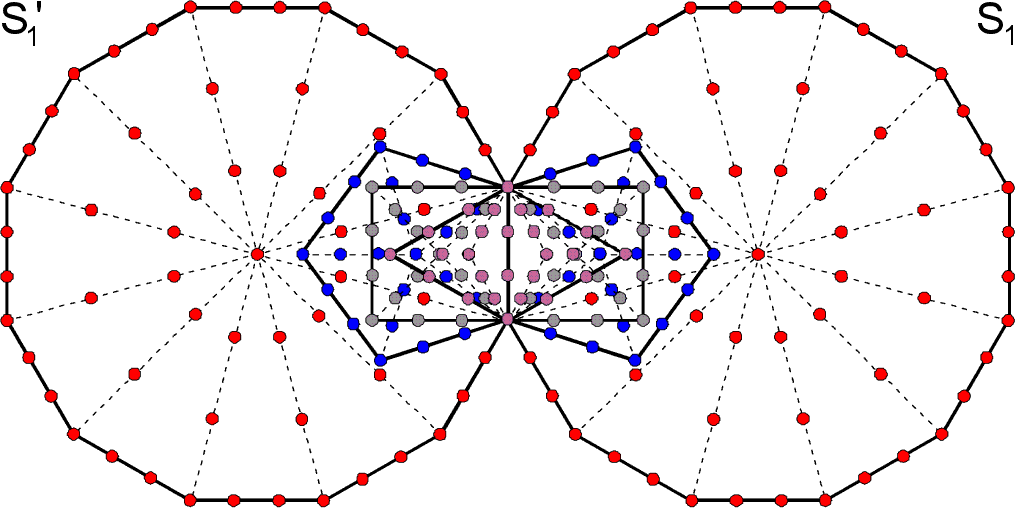
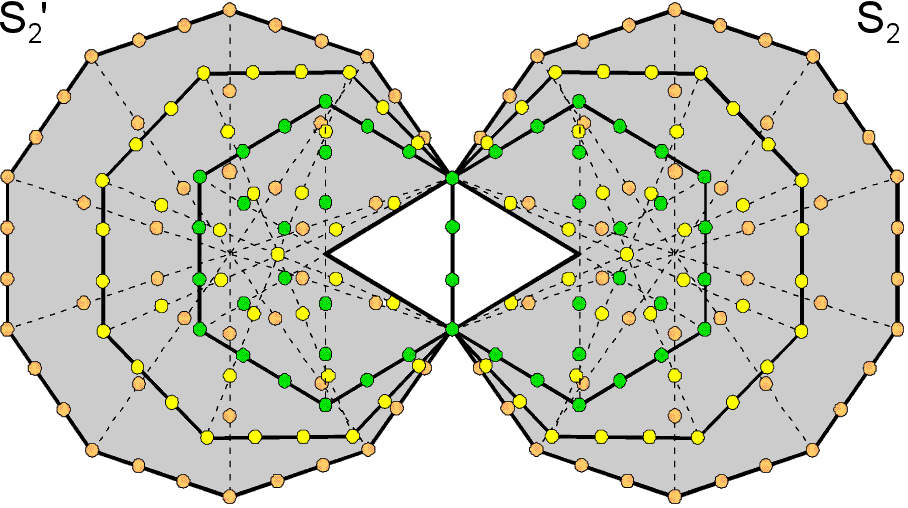
Elsewhere in this website, it has been pointed out that the seven separate polygons with 48 corners comprise two sets of polygons with 24 corners: the first set (let us call it S1) consists of the triangle, square, pentagon & dodecagon; the second set (call it S2) consists of the hexagon, octagon & decagon:
 |
 |
(remember that in situ, S2 has the sector missing that is occupied by the violet triangle in S1). This 24:24 division of the parameter 48 is characteristic of all holistic systems. It manifests in the 4-dimensional projection of the 421 polytope as the 120 vertices in each of the two 600-cells whose compound is the 4-dimensional projection of this polytope in the Coxeter plane (see here). This is because the 120 hexagonal yods in the four separate polygons of S1 symbolise the 120 vertices in one 600-cell and the 120 hexagonal yods in the three polygons of S2 symbolise the 120 vertices in the other 600-cell. If the inner form of the Tree of Life is thought of as the "DNA" encoding how its outer form replicates, then S1 and S2 are the "strands" of this DNA and have their microscopic realisation in the outer and inner halves of the 10 helical whorls of the UPA/E8×E8 heterotic superstring, the two halves being generated by the 240 vertices of the two 600-cells (or, rather, the 240 E8 gauge charges that they represent). It is worthwhile, therefore, to examine the geometrical and yod compositions of S1 and S2.
Geometrical composition of S1 & S2
When they are
separate, S1 and S2 have the same number of corners and the same number of
sides. Enfolded and associating the root edge with S1, both S1 and
S2 have 18 corners and 21 sides. In terms of just their boundaries, they
are the two halves of half the inner Tree of Life. Listed in Table 1 are the numbers of corners, sides &
triangles in the seven separate, regular polygons when they are divided into their sectors:
Table 1. Geometrical composition of the seven separate Type A polygons.
|
Triangle |
Square |
Pentagon |
Hexagon |
Octagon |
Decagon |
Dodecagon |
Total |
|
|
Corners |
4 |
5 |
6 |
7 |
9 |
11 |
13 |
55 |
|
Sides |
6 |
8 |
10 |
12 |
16 |
20 |
24 |
96 |
|
Triangles |
3 |
4 |
5 |
6 |
8 |
10 |
12 |
48 |
|
Total |
13 |
17 |
21 |
25 |
33 |
41 |
49 |
199 |
Table 2 lists the geometrical compositions of the root edge and what is outside it in S1 and S2 with enfolded polygons:
Table 2. Geometrical composition of S1 & S2 outside the root edge.
|
Root edge |
S1 |
S2 |
Total |
|
|
Corners |
2 |
20 |
19 |
41 |
|
Sides |
1 |
44 |
43 |
88 |
|
Triangles |
0 |
24 |
23 |
47 |
|
Total |
3 |
88 |
85 |
176 |
S1 and S2 cannot have the same number of corners of their sectors because the total number (41) is an odd integer, not an even one. But, if we associate the root edge with S2, the latter has the same number of sides (44), as well as the same number of corners, sides & triangles (88), as S1. If we associate one endpoint of the root edge with one set of seven enfolded polygons and the other endpoint with its mirror image, then one endpoint can be regarded as belonging to S2 in each set, so that the 40 corners associated with each set comprise 20 corners in S1 and 20 corners in S2. This means that, outside the root edge, S1 has 44 corners & triangles and 44 sides, whilst S2 has 44 corners & triangles and 44 sides, including the root edge. Whether as combinations of just polygons or as combinations of polygons divided into their sectors, S1 and S2 can be regarded as the two halves of the set of seven enfolded polygons.
Superstring structural parameters 84, 168 & 336 embodied in
S1 & S2
According to Table 2, S1 has 88 geometrical elements outside the root edge, i.e., 84 elements
surround the centres of its four polygons. S2 has 85 geometrical elements outside the root
edge. Of these, one is the centre of the octagon, the two other centres belonging to S1, so that 84
geometrical elements surround the centres of its three polygons. Hence, S1 &
S2 comprise 168 geometrical elements outside the root edge that surround
their centres. The two S1 and the two S2 consist of
(168+168=336) geometrical elements outside the root edge that surround the
(5+5) centres that are not also corners of polygons:
|
|
 |
|
(84+84=168) geometrical elements surround the centres of the eight polygons in the two S1. |
(84+84=168) geometrical elements surround the centres of the 6 polygons in the two S2. |
Both the 84:84 division of the holistic parameter 168 and the 168:168 division of the holistic parameter 336 are discussed in many places of this website as characteristic of sacred geometries. The 8:6 division of the 14 regular polygons making up the inner Tree of Life splits in half the 336 intrinsic geometrical elements surrounding their centres. We find a similar division in the 14 types of notes that are found in the seven diatonic scales (see The seven musical scales). Eight of them constitute the Pythagorean octave and six are non-Pythagorean notes. It occurs also in the outermost group of 14 triangles of the Sri Yantra. Six of these triangles touch the circular ring of eight lotus petals that surrounds the 43 triangles and eight triangles do not touch it (see here).
The inner Tree of Life has 336 intrinsic geometrical elements outside the root edge surrounding the centres of its 14 polygons. It is divided into two halves (S & S′), with S′ the mirror image of S. Each half has 168 geometrical elements and is further split into two halves: S1 & S2. Let us label as S1′ the mirror image of S1 and as S2′ the mirror image of S2. Each "quarter" of the inner Tree of Life has 84 geometrical elements surrounding centres of polygons. Compare this with the following structural properties of the UPA: each helical whorl with 1680 turns twists five times around the axis of spin. It makes five half-revolutions, each of 168 helical turns, in the larger spiral of its outer half and five half-revolutions, each of 168 turns, in the narrower spiral of its inner half. Each turn is a circularly polarised oscillation consisting of two perpendicular plane waves vibrating 90° out of phase, so that a half-revolution comprises 336 plane wave oscillations grouped into 168 pairs. A factor of 2 manifests in a half-revolution of a whorl, firstly, as its two quarter-halves and, secondly, as the two perpendicular oscillations generating each turn. Two schemes of correspondence between the inner Tree of Life and a half-revolution of a whorl are possible:
|
Case A |
Case B |
||
|
168 oscillations |
→ |
168 geometrical elements in S |
168 geometrical elements in S1 & S1′ |
|
168 oscillations with 90° phase difference |
→ |
168 geometrical elements in S′ |
168 geometrical elements in S2 & S2′ |
|
84 oscillations in first ¼-revolution |
→ |
84 geometrical elements in S1 |
84 geometrical elements in S1 |
|
84 oscillations in first ¼-revolution with 90° phase difference |
→ |
84 geometrical elements in S1′ |
84 geometrical elements in S2 |
|
84 oscillations in second ¼-revolution |
→ |
84 geometrical elements in S2 |
84 geometrical elements in S1′ |
|
84 oscillations in second ¼-revolution with 90° phase difference |
→ |
84 geometrical elements in S2′ |
84 geometrical elements in S2′ |
Intuitively speaking, case A seems the correct correspondence, with S1 and S2 denoting the two quarter-revolutions and the two halves of the inner Tree corresponding to the two plane wave oscillations that are 90° out of phase. This is because each half of the inner form of the Tree of Life constitutes a whole in itself and is a more fitting representation of each set of 168 orthogonal plane waves that makes up the half-revolution of a whorl. This is consistent with the Tree of Life nature of a whorl because the latter makes 10 half-revolutions around the spin axis of the UPA, each being analogous to one of the 10 Sephiroth, so that a whorl is represented by 10 Trees of Life, each corresponding to a Sephirah, and its 10 half-revolutions are also represented by 10 overlapping Trees. The analogy between the geometries of the inner Tree of Life and the UPA is summarised below:
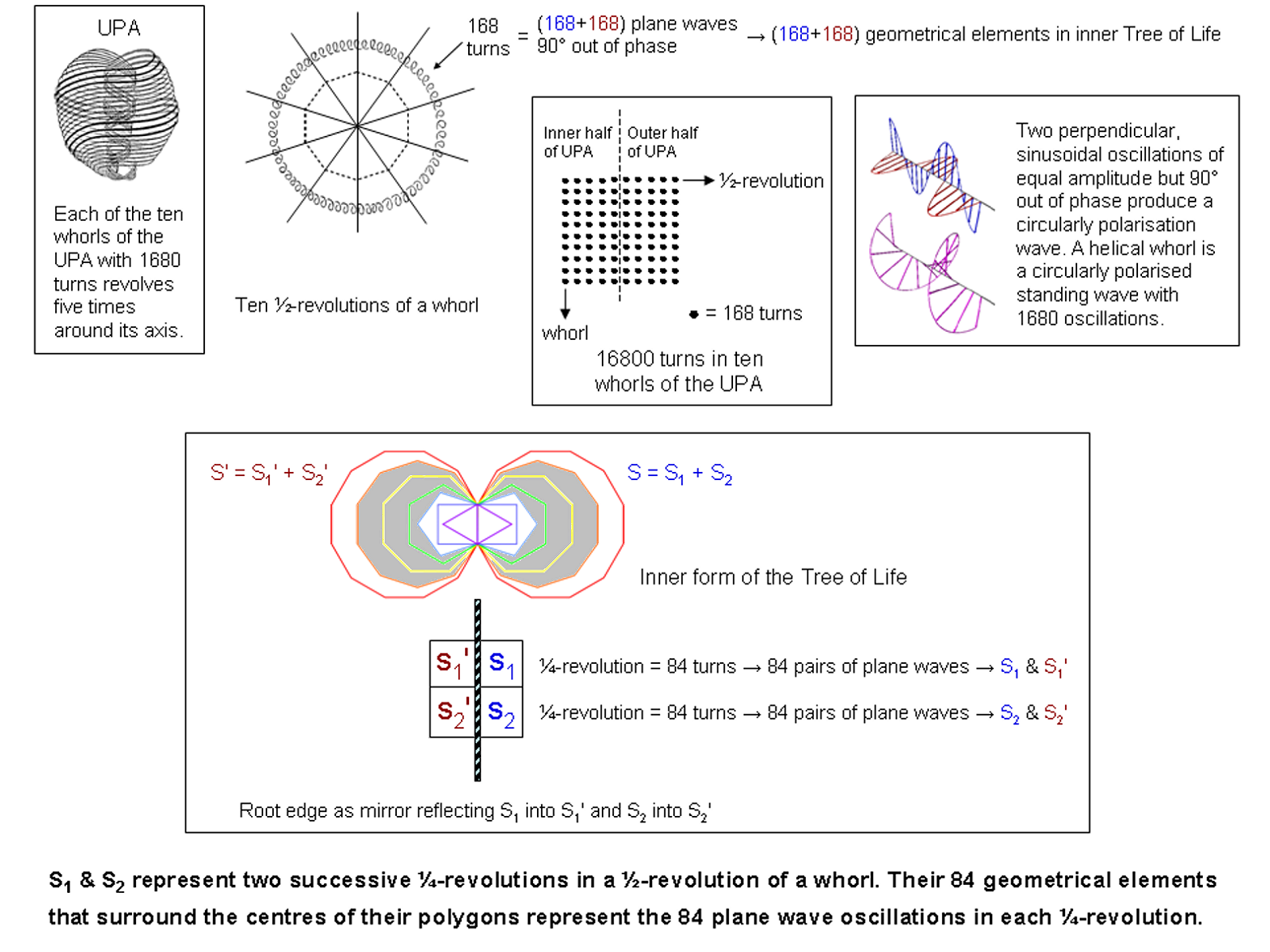 |
That there are four components of the inner Tree of Life and that each half of it results from pairing of these components only in one way:
S1 ↔ S2 and S1′ ↔ S2′,
not
S1 ↔ S2′ or S2 ↔ S1,′
reminds us of the four types of nitrogen bases in the DNA molecule: A, T, G & C, and how base A always pairs with base T through two hydrogen bonds and base C with base G through three hydrogen bonds when they form a rung of base pairs in the helical DNA ladder. It is as though the complementary pairs of bases (A, T) and (C, G) are analogous, respectively, to (S1, S2) and (S1′, S2′), so that the two helical halves of the DNA molecule are analogous to the two sets of sinusoidal waves in each helical whorl that generate its 1680 circularly polarised waves because the waves in one set are 90° out of phase with those in the other set. Each turn in a whorl would then correspond to a rung of base pairs, whilst the complementary nitrogen bases at each end of each rung would correspond to the two sinusoidal oscillations of the same amplitude but 90° out of phase that constitute a turn. The pairing of complementary bases in the molecule of life is an expression of the Taoist principle that the yang aspect of nature is always balanced with its yin aspect. The supposition of two orthogonal sinusoidal oscillations in every turn of a whorl is another manifestation of this cosmic balance. In the inner form of the Tree of Life, it is expressed by its two halves, one associated with the right-hand Pillar of Mercy, which embodies the active, 'male' principle (Shiva, or Yang), and the other associated with the left-hand Pillar of Judgement, which embodies the receptive, 'female' principle (Shakti, or Yin). The terms 'male' and 'female' are, of course, used here in their metaphysical sense, not the more familiar, psycho-sexual connotation. Their corresponding meanings in physics are, respectively, force and matter, or kinetic energy and potential energy.
Yod populations of S1 & S2
Let us now consider the yod compositions of S1 and S2. Listed in Table 3 are the
numbers of yods in the seven separate, regular polygons whose sectors are constructed from
tetractyses:
Table 3. Yod populations of the seven separate, Type A polygons.
|
Triangle |
Square |
Pentagon |
Hexagon |
Octagon |
Decagon |
Dodecagon |
Total |
|
|
Corners |
4 |
5 |
6 |
7 |
9 |
11 |
13 |
55 |
|
Hexagonal yods |
15 |
20 |
25 |
30 |
40 |
50 |
60 |
240 |
|
Total |
19 |
25 |
31 |
37 |
49 |
61 |
73 |
295 |
Table 4 lists the yod populations of the root edge and what is outside it in S1 and S2:
Table 4. Yod compositions of S1 & S2 outside the root edge.
|
|
Root edge |
S1 |
S2 |
Total |
|
Corners |
2 |
20 |
19 |
41 |
|
Hexagonal yods |
2 |
112 |
109 |
223 |
|
Total |
4 |
132 |
128 |
264 |
If we associate the root edge and its four yods with S2, the latter has the same number of yods (132) as S1. In other words, the yod population of the seven enfolded polygons then becomes evenly divided between S1 and S2, just as we saw earlier that their number of geometrical elements is. The split of the seven separate polygons into two sets with the same numbers of corners, sides & triangles surrounding their centres and the same numbers of yods surrounding their centres persists in the seven enfolded polygons in the form of S2 having the same number of yods as S1 has outside the root edge.
From the numbers of corners of the seven regular polygons making up the inner Tree of Life:
3, 4, 5, 6, 8, 10, 12
four combinations of numbers add up to 24:
The seven polygons can be divided into either combinations 1 and 2 or 3 and 4. Combinations 1 & 2 are, respectively, S1 and S2. Let us call combinations 3 & 4, respectively, "S3" & "S4". The geometrical compositions of the root edge and what is outside it in S3 and S4 are shown in Table 5:
Table 5. Geometrical compositions of S3 & S4 outside the root edge.
|
Root edge |
S3 |
S4 |
Total |
|
|
Corners |
2 |
18 |
21 |
41 |
|
Sides |
1 |
42 |
45 |
88 |
|
Triangles |
0 |
23 |
24 |
47 |
|
Total |
3 |
83 |
90 |
176 |
We see that the geometrical compositions of S3 and S4 (either for each type of geometrical element or in total) cannot be made equal by associating the three geometrical elements in the root edge with either total for S3 and S4. Listed below in Table 6 are their yod populations:
Table 6. Yod populations of S3 & S4 outside the root edge.
|
Root edge |
S3 |
S4 |
Total |
|
|
Corners |
2 |
18 |
21 |
41 |
|
Hexagonal yods |
2 |
107 |
114 |
223 |
|
Total |
4 |
125 |
135 |
264 |
We see that their various yod populations cannot be made equal by associating the four yods in the root edge with either S3 or S4. Only the 24:24 division of the seven separate polygons into S1 and S2 creates equal total numbers of geometrical elements and equal yod populations when the two combinations with 24 polygonal corners become enfolded. This remarkable fact provides additional support for making use of only these two combinations in various analyses of the inner Tree of Life basis of holistic parameters, such as the superstring structural parameters 1680, 336 & 168. As this has shown, they are in fact the only two combinations that have equal populations of geometrical elements and yods.
Further evidence of the unique status of S1 and S2 vis-à-vis the inner Tree of Life is provided by S1 & S1′ and S2 & S2′ making up the (7+7) enfolded polygons. According to Table 4, S1 & S1′ have (2×132=264) yods outside the root edge and S2 & S2′ have (2×128=256=44) yods outside the root edge, i.e., 260 yods when the latter is included. The seven enfolded polygons have 264 yods, of which 260 yods lie outside the root edge:
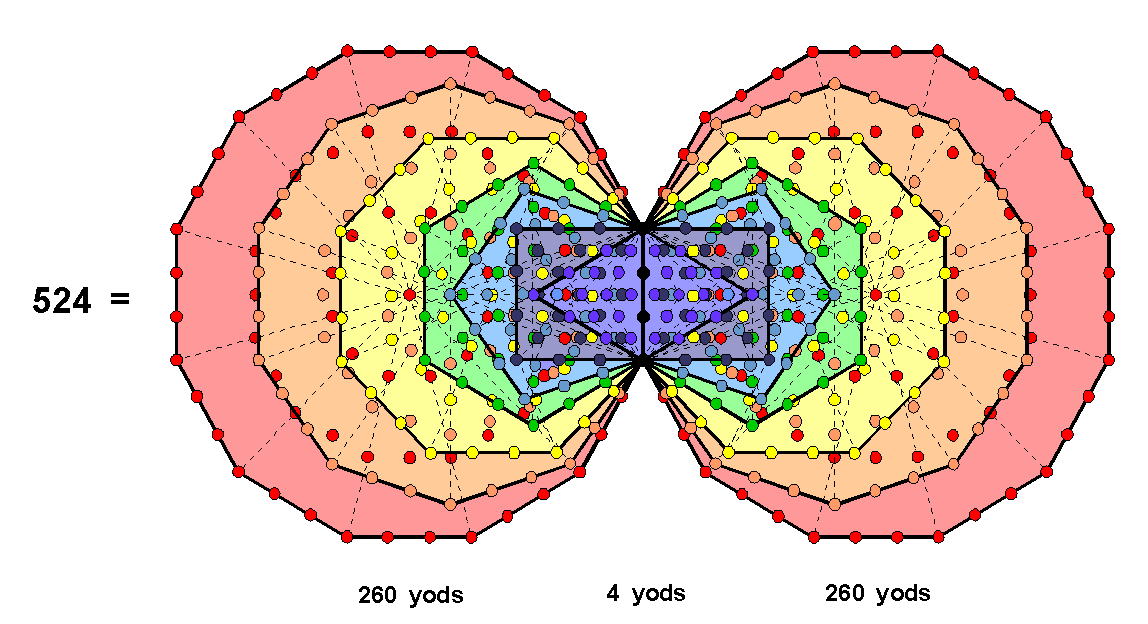
S1 & S1′ without the root edge have the yod population of the seven enfolded polygons, i.e, one half of the inner Tree of Life, and S2 & S2′ with the root edge have the yod population of the seven enfolded polygons outside their root edge. Table 7 lists the numbers of yods lining the tetractyses in S1 and S2:
Table 7. Numbers of boundary yods in S1 & S2.
| S2′ | S1′ | Root edge | S1 | S2 | |
| Yod population | 128 | 132 | 4 | 132 | 128 |
| Number of hexagonal yods at centres of tetractys | 23 | 24 | − | 24 | 23 |
| Number of boundary yods | 105 | 108 | 4 | 108 | 105 |
S1 & S1′ have 216 boundary yods outside the root edge. The seven enfolded polygons have 264 yods, of which 47 are hexagonal yods at centres of tetractyses. This leaves 217 boundary yods, of which one is the top of the hexagon and coincides with the lowest corner of the hexagon enfolded in the inner form of the next higher Tree of Life. It means that 216 yods lining the sides of tetractyses are intrinsic to the inner form of each overlapping Tree. This is the number of boundary yods in S1 & S1′.
 |
 |
|
216 yods intrinsic to one set of 7 enfolded polygons line their 47 tetractys sectors. |
216 yods outside the root edge line the 48 tetractyses in S1 & S1′. |
|
|
 |
| The Tree of Life contains 214 yods when its 16 triangles are Type A. | 214 yods line the 46 tetractyses in S2 & S2′. |
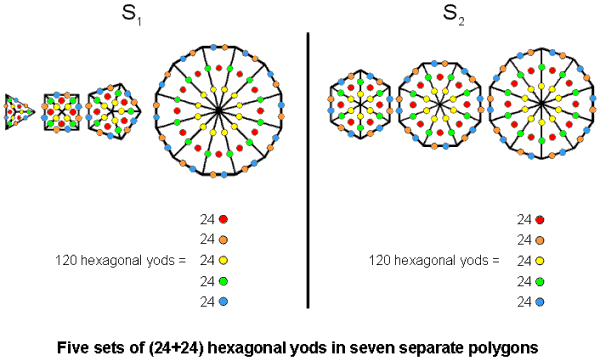
According to Table 7, S2 & S2′ have 214 boundary yods when the root edge is included. This is the number of yods in the outer Tree of Life with 16 Type A triangles (see diagram above). S2 has 109 boundary yods when the root edge is included. As it contains the hexagon, the topmost corner of which coincides with the lowest corner of the hexagon enfolded in the next higher Tree of Life, 108 such yods are intrinsic to S2. This is also the number of boundary yods in S1 outside the root edge. Not only are the yod populations of S1 & S2 equal, but so, too, are the numbers of yods on the boundaries of their tetractyses when the root edge is associated with S2. The 216 boundary yods intrinsic to the seven enfolded polygons are divided equally by S1 and S2, whilst the pair (S1, S1′) and the pair (S2, S2′) embody the same holistic parameter. It is further evidence that S1 & S2 uniquely embody properties that are quantified by the same numbers that quantify properties of the complete form of the inner Tree of Life. The implication of this is that these two halves of the inner Tree should be regarded as holistic structures in themselves. It should, therefore, come as no surprise that S1 & S2 can be regarded as representing the two 600-cells that are the two halves of the Petrie projection onto the Coxeter plane of the 421 polytope which in turn generate the outer and inner halves of the UPA, the subquark state of the E8×E8 heterotic superstring (see the discussion under Fig. 4 here). They can further be associated with the 120 vertices & edges of the 24-cell making up each 600-cell and with its 120 faces & octahedral cells, that is, with its 0- & 1-polytopes and with its 2- & 3-polytopes, for the polytopic composition of the 24-cell conforms to the archetypal pattern of the seven regular polygons in the inner Tree of Life (see beginning of #4 here). This 120:120 division exists in S1 & S2 not only when their polygons are regarded as enfolded but also when they are separate. The number of hexagonal yods in an n-gon is 5n, so that each combination of separate polygons has 5×24 = 120 yods. Assigning a different colour to each of the five hexagonal yods per sector of an n-gon, every colour appears 24 times in S1 and five times in S2. For the 600-cell, each hexagonal yod denotes a vertex of a 24-cell, the five colours signifying the five such cells whose compound is the 600-cell:
 |
 |
|
When consisting of Type A polygons, both S1 and S2 have 120 hexagonal yods grouped into 5 sets of 24. |
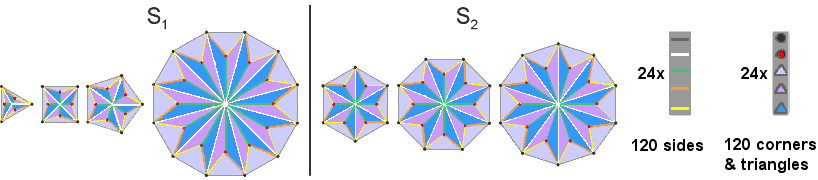
When consisting of Type B polygons, both S1 and S2 have 240 geometrical elements grouped into 5 sets of 24 sides and 5 sets of 24 corners & triangles. |
The number of corners, sides & triangles surrounding the centre of a Type B n-gon is 10n. The 10 geometrical elements per sector comprise five sides and five corners & triangles. The 240 geometrical elements in either S1 or S2 that surround centres of polygons comprise 120 sides and 120 corners & triangles. So they display the 120:120 division characteristic of holistic systems in both their sides and their corners & triangles. Whether we are speaking of hexagonal yods in Type A polygons or geometrical elements in Type B polygons, the number 240 is present. In the case of the latter polygons, because the 10 geometrical elements per sector divide naturally into two sets of five, S1 & S2, which are the two halves of the seven separate polygons whose centres are surrounded by 480 geometrical elements, each comprises 240 such elements. As the parameter 240 in sacred geometries always corresponds to the 240 roots of E8, we see that the two halves signify the two identical E8 Lie groups that appear in the direct product E8×E8, one of the two symmetry groups that were discovered in 1984 to describe the interactions of superstrings that are free of quantum anomalies. We saw earlier that, even though they are, separately, only half of the whole set of polygons making up the inner Tree of Life, S1 & S2 possess properties quantified by numbers that refer to this whole set. Here, once again, is evidence that S1 & S2 can be regarded as wholes in themselves. They remind one of the division of the Tao into the polar opposites of Yin and Yang — complementary components of the Whole, yet complete in themselves. S1 & S2 (each with 120 hexagonal yods in their separate polygons) can be thought of as corresponding in the outer Tree of Life to its right-hand and left-hand halves, which are shown here (see fourth picture) be composed of 120 yods other than the corners of its Type A triangles.
The two S2 embody the dimension 248 of E8
According to Table 4, S1 has 132 yods outside the root edge, where 132 = 4×33 = 4×(1!+2!+3!+4!).
S2 has 128 yods outside the root edge. This is the sum of the Godnames of the first
four Sephiroth:
21 + 26 + 50 + 31 = 128.
S2 & S2′ have 256 yods outside the root edge, where 256 = 44. These properties demonstrate the role of the Tetrad in determining the yod populations of the two halves of the inner Tree of Life. Of the 128 yods in S2, six yods lie on the two vertical sides of tetractyses inside the hexagon that are shared with triangles in the outer Tree of Life because these sides form its Pillar of Mercy and its Pillar of Judgement.* (128−6=122) yods outside the root edge are intrinsic to S2. Including the root edge, the number of yods intrinsic to S2 & S2′ in the inner form of the Tree of Life = 4 + 2×122 = 248. This is the dimension of E8. Of the 132 yods in S1, one yod (the right-hand corner of the triangle) is shared with the outer Tree because it coincides with the Sephirah Chesed; this leaves 131 intrinsic yods. 131 is the number value of Samael, the Archangel of Geburah, whose number 216 was found earlier to be the number of yods lining the 48 tetractyses in S1 & S1′ where 48 is the number of Kokab, the Mundane Chakra of Hod.
The significance of the S1:S2 division for CTOL
According to Table 3, the seven separate Type A polygons have 295 yods. 288 yods surround their centres, where
288 = 1!×2!×3!×4!.
As revealed on #5 of Maps of reality/Cosmic Tree of
Life, there are 295 SLs up to Chesed of the 49th Tree. Chesed is the first of the seven
Sephiroth of Construction. The 49th Tree is the first of the 49 Trees
mapping the 49 subplanes of the seven planes of consciousness that correspond to these
Sephiroth. As each Tree expresses the essence of a Sephirah of Construction, the 49th Tree
expresses Chesed. So the 295th SL expresses par excellence the quality of this Sephirah, being
Chesed of the Tree that most corresponds to Chesed. Each yod in a polygon denotes one of the 295 SLs up to the
starting point for the 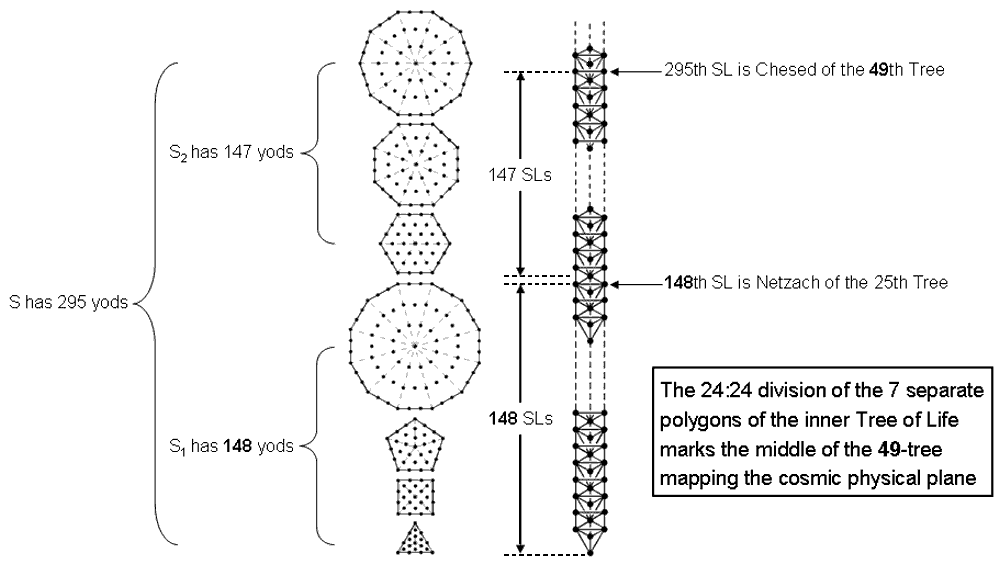 emanation of the 49-tree representing the cosmic physical plane. According to
Table 3, the four separate polygons in S1 contain 148 yods and
S2 has 147 yods. The S1:S2 division therefore splits in half the
yod population of the seven separate polygons of the inner Tree of Life. The 148th SL is
Netzach of the 25th Tree, which is the middle of the lowest 49 Trees,
having 147 SLs below and above it up to Chesed of the 49th Tree. The number 148 is the gematria number value of Netzach. The
25th Tree maps the fourth subplane of the fourth plane of consciousness, both
subplane and plane corresponding to Netzach, the fourth Sephirah of Construction. Hence, the
number 148 — the halfway point in the emanation of the 295 SLs — locates the very SL in
the 49-tree that most expresses this Sephirah, just as the number 295 locates the SL in CTOL
that is most expressive of the Sephirah Chesed! This remarkable property cannot be a mere coincidence.
Instead, the 24:24 division of the seven polygons, which divides the 168 intrinsic
geometrical elements surrounding their centres into two sets of 84 elements, also divides in half the SLs that
their yods symbolise, namely, those that belong to the 49 Trees mapping the cosmic
physical plane.
emanation of the 49-tree representing the cosmic physical plane. According to
Table 3, the four separate polygons in S1 contain 148 yods and
S2 has 147 yods. The S1:S2 division therefore splits in half the
yod population of the seven separate polygons of the inner Tree of Life. The 148th SL is
Netzach of the 25th Tree, which is the middle of the lowest 49 Trees,
having 147 SLs below and above it up to Chesed of the 49th Tree. The number 148 is the gematria number value of Netzach. The
25th Tree maps the fourth subplane of the fourth plane of consciousness, both
subplane and plane corresponding to Netzach, the fourth Sephirah of Construction. Hence, the
number 148 — the halfway point in the emanation of the 295 SLs — locates the very SL in
the 49-tree that most expresses this Sephirah, just as the number 295 locates the SL in CTOL
that is most expressive of the Sephirah Chesed! This remarkable property cannot be a mere coincidence.
Instead, the 24:24 division of the seven polygons, which divides the 168 intrinsic
geometrical elements surrounding their centres into two sets of 84 elements, also divides in half the SLs that
their yods symbolise, namely, those that belong to the 49 Trees mapping the cosmic
physical plane.
Here is confirmation of this conclusion: the numbers of corners, sides, triangles & tetrahedra making up the n-tree are shown below:
Number of corners = 6n + 5.
Number of sides = 16n + 9
Number of triangles = 12n + 7.
Number of tetrahedra = n +1.
Total number of geometrical elements in the n-tree = 35n + 22.
Every 48 overlapping Trees contain (48×35=1680) geometrical elements and every 24 Trees contain 840 elements. Dividing any section of 48 Trees into two sets of 24 Trees generates two sets of 840 geometrical elements. Apart from the Pythagorean factor of 10, here is the 84:84 division of geometrical elements found earlier for the division of the seven polygons with 48 corners into S1 and S2, each with 24 corners. Their counterparts in the UPA are the 840 turns in either an outer or inner half of a single whorl or in a quarter-revolution of all 10 whorls.
This mathematical analogy between the subquark superstring and the cosmic physical plane is a beautiful illustration of the hermetic principle: "As above, so below." Itconstitutes undeniable evidence that the Theosophical doctrine of the seven planes of consciousness is correct, for it is implausible in the extreme to dismiss as coincidence both the facts that S1 and S2 mark not only the middle of the seven regular polygons making up the inner Tree of Life but also the centre of the 49-tree representing the 49 subplanes of the seven planes of the spiritual cosmos.
For a discussion of the counterparts of S1 and S2 in other sacred geometries, see Article 64.