ARTICLE 9

by

Stephen M. Phillips

Flat 4, Oakwood House, 117-119 West Hill Road. Bournemouth. Dorset BH2 5PH. England. 

Website: http://smphillips.mysite.com

 

Abstract

 

1. Introduction
The Pythagorean mathematician Nichomachus of Gerasa said that the Pythagoreans called the number 4, or Tetrad, "the greatest miracle," "a God after another manner," "a manifold divinity," and "holding the key of Nature." Why did he (and his precursors) value this number so highly? Lacking insight into the mystical wisdom of ancient sages like Pythagoras and possessing only a few surviving written fragments of his teachings — themselves only elementary and distorted summaries of a now lost knowledge taught by word of mouth — modern scholarship has no satisfactory answer to this question. Historians of Greek mathematics realise that the

1

 

early Pythagoreans placed special emphasis on the number 4 because their so-called 'perfect number' 10 is the fourth triangular number, otherwise known as the 'tetractys' (from the Greek word 'tetras,' meaning 'four'):

They knew also that the numbers 1, 2, 3 & 4 contain the symphonic ratios that make possible the musical scale, i.e. 1:2, the octave; 2:3, the perfect fifth; and 3:4, the perfect fourth. But the true reason why the Pythagoreans valued the tetrad so highly was far more profound. They intuitively recognised that a four-fold pattern or structure existed in the mathematics of the cosmos, generating not only the number 10 as the measure of divine perfection and the tetractys as its symbol of wholeness but also numbers that quantify physical phenomena. This rule was formulated as the ‘Tetrad Principle’ in Article 1, which showed how parameters of superstring theory have a natural expression in terms of the numbers 1, 2, 3 & 4 — even the number 4 itself.

In this article it will be explained how the square, the geometrical symbol of the number 4, embodies certain numbers of relevance to superstring theory (and beyond), thus amply justifying the assignment to the Tetrad by the Pythagoreans of the title “holding the key of Nature.”

2. The square encodes 25 spatial dimensions & dimension 248 of E₈

When its sectors are tetractyses, a square contains 25 yods:

They symbolise the 25 dimensions of space predicted by the quantum mechanics of spinless (bosonic) strings. The number 16 (4th square number) is the number of purely bosonic string dimensions of the 26-dimensional space-time whose compactification, according to the author’s theory outlined in Article 2, generates superstrings with 9 remaining spatial dimensions (9 = 4th odd integer after 1). The central yod () symbolises the longitudinal dimension of a bosonic string, the surrounding 24 (=1×2×3×4=4!) yods represent the 24 transverse dimensions of a string and the surrounding 8 yods () denote the 8 transverse, purely superstring dimensions (8 = 4th even integer). 25 is the arithmetic mean of the cubes of the first 4 integers:

25 = (1³ + 2³ + 3³ + 4³)/4.

When the cubes of the integers 1, 2, 3 & 4 are assigned to the positions of the 25 yods in a square, their sum:

is the dimension of the unified, superstring gauge symmetry group E₈. In other words, the square not only encodes the number of spatial dimensions of space-time but also embodies the number of quantum states

2

 

Table 1. Gematria number values of the ten Sephiroth in the four Worlds.

	SEPHIRAH	GODNAME	ARCHANGEL	ORDER OF ANGELS	MUNDANE CHAKRA
1	Kether (Crown)   620	EHYEH (I am)   21	Metatron (Angel of the Presence)   314	Chaioth ha Qadesh (Holy Living Creatures)   833	Rashith ha Gilgalim First Swirlings. (Primum Mobile)    636
2	Chokmah (Wisdom)    73	YAHWEH, YAH (The Lord)   26, 15	Raziel (Herald of the Deity)    248	Auphanim (Wheels)   187	Masloth (The Sphere of the Zodiac)   140
3	Binah (Understanding)   67	ELOHIM (God in multiplicity)    50	Tzaphkiel (Contemplation of God)   311	Aralim (Thrones)   282	Shabathai Rest. (Saturn)    317
	Daath (Knowledge)    474
4	Chesed (Mercy)   72	EL (God)   31	Tzadkiel (Benevolence of God)   62	Chasmalim (Shining Ones)   428	Tzadekh Righteousness. (Jupiter)    194
5	Geburah (Severity)   216	ELOHA (The Almighty)   36	Samael (Severity of God)   131	Seraphim (Fiery Serpents)   630	Madim Vehement Strength. (Mars)   95
6	Tiphareth (Beauty)   1081	YAHWEH ELOHIM (God the Creator)   76	Michael (Like unto God)   101	Malachim (Kings)   140	Shemesh The Solar Light. (Sun)   640
7	Netzach (Victory)   148	YAHWEH SABAOTH (Lord of Hosts)   129	Haniel (Grace of God)   97	Tarshishim or Elohim   1260	Nogah Glittering Splendour. (Venus)   64
8	Hod (Glory)   15	ELOHIM SABAOTH (God of Hosts)   153	Raphael (Divine Physician)   311	Beni Elohim (Sons of God)   112	Kokab The Stellar Light. (Mercury)   48
9	Yesod (Foundation)   80	SHADDAI EL CHAI (Almighty Living God)   49, 363	Gabriel (Strong Man of God)   246	Cherubim (The Strong)   272	Levanah The Lunar Flame. (Moon)   87
10	Malkuth (Kingdom)   496	ADONAI MELEKH (The Lord and King)   65, 155	Sandalphon (Manifest Messiah)   280	Ashim (Souls of Fire)    351	Cholem Yesodoth The Breaker of the Foundations. The Elements. (Earth)    168

 

The Sephiroth exist in the four Worlds of Atziluth, Beriah, Yetzirah and Assiyah. Corresponding to them are the Godnames, Archangels, Order of Angels and Mundane Chakras (their physical manifestation). This table gives their number values obtained by the ancient practice of gematria, wherein a number is assigned to each letter of the alphabet, thereby giving a number value to a word that is the sum of the numbers of its letters. Where they appear in the text, they are written in boldface.

3

 

 

of the particle transmitting the unified force between superstrings! Superstring theory, of course, predicts not 25 but nine spatial dimensions of space-time. Unless one is willing to dismiss as coincidence the appearance of the number 248 along with the number 25 and its break-down into the numbers 9 & 16, it indicates that superstrings and their gauge symmetry group E₈ have their origin in 26-d, not 10-d, spacetime.

That the number 26 should be connected to the number 248 is less surprising when it realised that it is the number value of YAHWEH, the Godname of Chokmah (Table 1).¹ The Godnames of the Sephiroth of the Tree of Life were shown in previous articles to prescribe the sacred geometries of its outer and inner forms, which were also shown to embody the number 248. That the number 26 should have fundamental scientific significance is indicated by the Tetrad Principle formulated in Article 1 (1), for it is the sum of the first four Mersenne numbers (2), that is, the sum of the combinations of 10 objects arranged in the four rows of a tetractys:

A B C D E F G H I J

Number of combinations   21 – 1 = 1   22 – 1 = 3   23 – 1 = 7   24 – 1 = 15  TOTAL = 26

There is also a remarkable arithmetic relationship between the two numbers. Using the identity:

6200 = 248×25 = 2² + 3² + 4² + ... + 26²,

where the first term, 2² = 4, is the Tetrad, we see that the square displays the following remarkable property of the number 248:

Starting with the Tetrad, 2² = 4, at the centre of the square and assigning the 24 (=1×2×3×4) squares 3² , 4² , ... 26² to the surrounding 24 yods of the four tetractyses, with squares of even integers inside the square and squares of odd integers on its boundary, the sum of these 25 squares is that resulting from assigning the number 248 to each yod in the square. This demonstrates the unique significance of the superstring parameter 248 vis-à-vis the square.

The dimension 496 of the superstring gauge symmetry groups E₈×E₈ and SO(32) that apply to the five superstring theories is the sum of the cubes of the first four odd integers:

This means that it can also be represented by a 4×4 square array of the squares of 1, 3, 5 & 7. It is an illustration par excellence of the Tetrad Principle.

The square encodes the number 248 geometrically as well as arithmetically, as now explained. Starting

___________________________
¹ Henceforth, all numbers in this table are written in boldface.

4

from the point, or Pythagorean Monad, the tetractys has ten points (symbolised below by circles), each of which is a potential tetractys of ten points, and so on.

Let us call the point the 0th-order tetractys, the tetractys known to mathematicians as the fourth triangular number the 1st-order tetractys, the next member of the infinite sequence the 2nd-order tetractys, etc. The number of yods in the 2nd-order tetractys shown above is:

85 = 4⁰ + 4¹ +4² + 4³

This is a property of the Pythagorean representation of holistic systems that illustrates the Tetrad Principle. The number of white yods (o) at corners of the ten tetractyses is 15, which is both the number of combinations of four objects and the fourth Mersenne number

Figure 1. The 40 tetractyses in the square when its sectors are 2nd-order tetractyses contain 248 coloured yods other than the 41 corners. These hexagonal yods, which symbolise the Sephiroth of Construction, denote the 248 gauge fields transmitting the unified force between superstrings.

(see earlier). The number of coloured yods is

70 =	7 7 7 7 7 7 7 7 7 7 ,

where 7 is the fourth odd integer. 70 is the fourth, 4-dimensional, tetrahedral number after 1, i.e., it is the number of balls that can be piled up in 4-dimensional space to form a four-dimensional tetrahedron.

Consider now a square divided into its four sectors, each of which is the 2nd-order tetractys (Fig. 1). The number of tetractyses is

40 =	4 4 4 4 4 4 4 4 4 4

as is the number of corners surrounding the centre of the square. The number of yods surrounding the centre of the square is

288 = 1¹ + 2² + 3³ + 4⁴.

Notice how the Tetrad expresses the properties of both the 2nd-order tetractys and the square when the latter is constructed from the former. There are 72 yods per sector, of which 10 are corners and 62 are coloured yods (what in earlier articles were referred to as “hexagonal yods,” so-called because they are located at the centres and corners of hexagons) . 72 is the number of Chesed and 62 is the number value of

5

 

Tzadkiel , the Archangel of Chesed. There are 48 yods lining the square, where 48 is the number value of Kokab, the Mundane Chakra of Hod. 80 corners & centres of tetractyses surround the centre of the square, where 80 is the number value of Yesod. 49 yods line its diagonals, where 49 is the number value of EL ChAI, the Godname of Yesod. 64 hexagonal yods line the edges of the 2nd-order tetractyses, where 64 is the number value of Nogah, the Mundane Chakra of Netzach. Fig. 1 shows that there are 248 hexagonal yods (yods other than corners of tetractyses). 248 is the number value of Raziel, the Archangel of Chokmah. Symbolising Sephiroth of Construction, they denote the 248 gauge fields of the superstring gauge symmetry group E₈ transmitting the unified force between superstrings. It is a remarkable demonstration of the way in which the Tetrad determines numbers of scientific significance, in this case the dimension of E₈. The Godname EHYEH prescribes it because the 36 tetractyses have 21 corners.

There are 32 hexagonal yods lying on the sides of the square that are unshared with adjacent tetractyses. This leaves (248–32=216) hexagonal yods inside the square. There are 46 internal hexagonal yods per sector that are unshared. The number of unshared hexagonal yods in the square = 32 + 4×46 = 216. It is amusing that this is the number of years that, according to Androcydes, the Pythagorean writer of the work On Symbols, and others was thought in antiquity to elapse between successive lives of Pythagoras. 216 is the number value of Geburah, the fifth

 Figure 2. Symbol of the Pythagorean Tetrad, the square can be formed from 36 tetractyses with 21 corners and with 168 yods surrounding its centre.

Sephirah (see Table 1). It is also the notorious number mentioned by Plato in a passage in his Republic, which is thought (3) to refer to its property as the sum of the cubes of the numbers 3, 4 & 5 that measure the sides of Pythagoras’ famous right-angled triangle.

Of the 48 yods on the boundary of the square whose sectors are divided into the next higher-order tetractys, four are its corners, leaving 44 other yods, once again illustrating the influence of the Tetrad in determining or expressing the properties of objects with sacred geometry.

6

 

3. Square encodes superstring structural parameter 168
In previous articles, it was explained how the outer and inner forms of the Tree of Life encode the number 168, which is the number value of Cholem Yesodoth, the Mundane Chakra assigned to Malkuth (physical universe). It is the number of circularly polarised waves making up half a revolution of each of the ten whorls of the superstring constituent of up and down quarks. We have already seen that the square encodes its dynamical parameter 248. It will now be shown how it embodies its structural parameter 168.

Instead of turning each sector of a square into a 2nd-order tetractys, consider it as a triangles divided into three sectors, each of which is then split into three more triangles turned into tetractyses (Fig. 2). Both a single square constructed in this way and the pair of squares enfolded in the inner form of the Tree of Life will be considered. Their properties are analysed below. Table 2 depicts the numbers in Table 1 that appear in the analysis presented in this article.

Table 2
(Numbers in coloured boxes appear in the discussion below)

Sephirah	Title	Godname	Archangel	Order of Angels	Mundane Chakra
Kether	620	21	314	833	636
Chokmah	73	15, 26	248	187	140
Binah	67	50	311	282	317
Chesed	72	31	62	428	194
Geburah	216	36	131	630	95
Tiphareth	1081	76	101	140	640
Netzach	148	129	97	1260	64
Hod	15	153	311	112	48
Yesod	80	49	246	272	87
Malkuth	496	65, 155	280	351	168

Single square
Square has four sectors, each with (3×3=9) triangles/tetractyses having 12 edges inside it.

Number of corners of triangles = 1 + 4 + 4×4 = 21 (19 outside root edge).
Number of sides of triangles = 4 + 4 + 4×12 = 56 (55 outside root edge, 48 not sides of sectors).
Number of triangles = 4×9 = 36.
Number of corners & sides of triangles = 21 + 56 = 77.
Number of corners & triangles = 21 + 36 = 57 (55 outside root edge).
Number of sides & triangles = 56 + 36 = 92 (91 outside root edge).
Number of corners, sides & triangles = 77 + 36 = 113 (113 – 3 = 110 outside root edge, 113 – 8 = 105 inside square).
Number of yods = 21 + 36 + 56×2 = 169 (169 – 4 = 165 outside root edge, 168 surrounding centre).
Number of yods at corners of tetractyses = 21.
Number of hexagonal yods = 169 – 21 = 148.
Number of yods on edges of tetractyses = 169 – 36 = 133 (133 – 4 = 129 yods outside root edge or generated from square with four corners).
Number of hexagonal yods on edges of tetractyses = 133 – 21 = 112.
Number of yods on boundary of square = 12.
Number of yods inside square = 169 – 12 = 157 (17 corners and 140 hexagonal yods).
Number of yods generated from square with 4 yods at corners = 169 – 4 = 165.
Two joined squares
Two squares have 8 sectors, each with (3×3=9) triangles/tetractyses with 12 edges inside it.

7

 

Number of corners of triangles = 2 + 2×19 = 40.
Number of sides of triangles = 1 + 2×55 = 111 (110 outside root edge).
Number of triangles = 2×36 = 72.
Number of corners & sides of triangles = 40 + 111 = 151.
Number of corners & triangles = 40 + 72 = 112.
Number of sides & triangles = 111 + 72 = 183.
Number of corners, sides & triangles = 151 + 72 = 223 (223 – 3 = 220 outside root edge, 223 – 13 = 210 inside squares).
Number of yods = 4 + 2×165 = 334 (334 – 4 = 330 outside root edge).
Number of yods at corners of tetractyses = 2 + 2×19 = 40.
Number of hexagonal yods = 334 – 40 = 294 (292 outside root edge).
Number of yods on edges of tetractyses = 334 – 72 = 262 (262 – 4 = 258 outside root edge).
Number of hexagonal yods on edges of tetractyses = 262 – 40 = 222 (220 outside root edge).
Number of yods on boundary of squares = 4 + 2×(12–4) = 20.
Number of yods inside squares = 334 – 20 = 314 (34 corners and 280 hexagonal yods, 140 in each square).
Number of yods generated from two joined squares with 6 corners = 334 – 6 = 328.

Listed below are the ways in which the number values of the Godnames of the 10 Sephiroth prescribe the properties of the square and the pair of joined squares:

Kether: 21	36 triangles in square have 21 corners. also, 210 (=21×10) corners, sides & triangles inside squares.
Chokmah: 15	Number of corners & sides of triangles = 151 = 150th integer after 1, where 150 = 15×10.
26	36 triangles in square have 56 sides, of which 52 are generated from square, where 52 = 26th even integer.
Binah: 50	Number of corners, sides & triangles in two squares separated by root edge = 3 + 2×113 = 229 = 50th prime number.
Chesed: 31	Number of new yods outside root edge on edges of tetractyses in square = 129 – 2 = 127 = 31st prime number. Also, number of yods outside root edge of two joined squares other than corners = 330 – 19 = 311 = 310th integer after 1, where 310 = 31×10.
Geburah: 36	Square has 36 triangles. also, two joined squares have 151 corners & sides, where 151 = 36th prime number.
Tiphareth: 76	Square has 77 corners & sides, where 77 = 76th integer after 1.
Netzach: 129	Number of yods in two joined squares outside root edge on sides of tetractyses = 258 = 129th even integer. Also, the number of yods generated from square with four corners.
Hod: 153	Number of corners & sides of two separate squares = 2×77 = 154 = 153rd integer after 1.
Yesod: 49	72 triangles in two joined squares have 111 sides, of which 14 are sides of sectors other than root edge. number of sides other than sector edges = 111 – 14 = 97 = 49th odd integer.
Malkuth: 65	129 yods outside root edge on sides of two squares, where 129 = 65th odd integer.
155	Number of yods inside square surrounding centre = 157 – 1 = 156 = 155th integer after 1.

The most important property listed above is that 168 yods surround the centre of a square whose sectors are constructed from three triangles, themselves constructed from three tetractyses. The number values of the Godnames of the ten Sephiroth therefore prescribe this basic structural parameter of the superstring.

The Pythagorean Tetrad determines the following properties of the square and the pair of joined squares present in the inner form of the Tree of Life:
1. Number of corners of tetractyses in two joined squares = 40

(10=1+2+3+4)

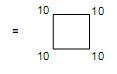
2. Number of sides outside the root edge of the square = 55

8

Figure 3. The fourth type of square has 168 yods surrounding its centre.

 

1       2 3 =   4 5 6       7 8 9 10.

(10=1+2+3+4)

This is also the number of corners and triangles in the square outside the root edge.
3. Number of corners, sides & triangles in two joined squares outside the root edge = 220

9

10

 

11

 

    4
      8 12
=    16 20 24
        28 32 36 40.

This is also the number of hexagonal yods outside the root edge in two joined squares.
1. Number of yods in the square = 169 = 13²

168 yods surround its centre, which is denoted by the number 1. 168 is the sum of the 12 odd integers after 1 on the square’s boundary, four to a side.
2. Number of yods in the square generated by its construction from tetractyses (i.e., yods other than its corners) = 169 – 4 = 165

Again, the central number, 1² = 1, denotes the centre of the square.
3. Number of yods outside the root edge of two joined squares = 330

The central number, 6² = 36, denotes the 36 hexagonal yods at the centres of the 36 tetractyses. The Tetrad also determines the superstring structural parameter 168 because it is the number of yods surrounding the centre of the fourth member of the sequence of tetractys-generated squares, starting with the square itself (Fig. 3). It is a remarkable illustration of the Tetrad Principle discussed in Article 1.

4. Equivalence of the square & the 7 enfolded polygons
According to the properties of the square listed in Section 2, the pair of squares has 262 yods on the boundaries of their 72 tetractyses. The seven regular polygons enfolded in the Tree of Life have 264 yods, that is, 262 yods are associated with either set of polygons. The number of yods defining the shapes of the tetractyses making up the pair of squares is that needed to fill up each half of the inner form of the Tree of

Figure 6. The number of hexagonal (i.e., new) yods in the Tree of Life constructed from tetractyses is the
number of yods needed to create a square, starting from its centre, with three tetractyses as each sector.

12

Life (Fig.4). Furthermore, there are 222 hexagonal yods on the boundaries of the 72 tetractyses. These yods correspond to the Sephiroth of Construction above Malkuth, the lowest Sephirah of Construction. 222 is the number of hexagonal yods associated with each set of seven enfolded polygons (Fig. 5). These two remarkable similarities demonstrate that the square possesses an implicit or hidden equivalence to the inner form of the Tree of Life. As there are 444 hexagonal yods in the (7+7) enfolded polygons (4), the Tetrad expresses the hexagonal yod population of the inner form of the Tree of Life.

The square is also equivalent in the same sense to the outer form of the Tree of Life. The reason for this is as follows: when the 16 triangles of the Tree of Life are turned into tetractyses, they contain 70 yods made up of the 10 corners of tetractyses at the positions of the Sephiroth and 60 hexagonal yods (Fig. 6). When each sector of a square is divided into three triangles which are then turned into tetractyses, the square is found to contain 61 yods. 60 yods are needed to construct such a transformed square from the point at its centre, just as 60 additional yods are required to construct the outer form of the Tree of Life from 16 tetractyses.

The hexagon is the fourth of the regular polygons. 36 yods surround its centre when its sectors are tetractyses. When the latter are of the same type as that discussed in Section 3 for the embodiment of the number 168 by the square, the hexagon contains 252 yods surrounding its centre.

Figure 7. The (248 + 248 ) yods outside the root edge surrounding the centres of the two joined hexagons symbolise the (248 + 248 ) gauge fields transmitting the unified
force between E₈×E₈ heterotic superstrings. The 78 green yods in each hexagon that are either centres or corners of tetractyses denote the 78 gauge fields of E₆.

Hence, there are 248 yods outside the root edge that surround its centre. Outside the root edge of the pair of joined hexagons (Fig. 7) are (248+248=496) yods surrounding their centres. They symbolise the (248+248) gauge fields of the E₈×E₈ heterotic superstring. Once again, we see how the Tetrad Principle picks out a mathematical object that embodies a number of fundamental significance. The regular polygon with four corners embodies the structural parameter 168 of superstrings and the fourth regular polygon embodies its dynamical parameters 248 & 496. ELOHA, the Godname of Geburah with number value 36, prescribes this representation because each hexagon has 36 yods surrounding its centre when its sectors are tetractyses. ELOHIM, Godname of Binah with number value 50, prescribes it because, including the four yods of the root edge, 500 (=50×10) yods surround the centres of the two hexagons. YAHWEH, the Godname of Chokmah with number value 26, prescribes this representation of the number 496 because 26 yods on edges of the sectors of each hexagon surround its centre. Each sector has nine hexagonal yods at the centres of tetractyses. There are (248 – 6×9 = 194) yods other than centres. 194 is the number value of Tzadekh, the Mundane Chakra of Chesed. The nine tetractyses in each sector have four corners inside the boundary of the hexagon (48 for both hexagons), which has four corners outside the root edge. Hence, there are (6×4 + 4 + 1 = 29) external corners and (248–28=220) hexagonal yods, where 220 = 4×55

         4
           8 12
=        16 20 24
            28 32 36 40,

13

showing how the Tetrad determines this number. The two joined hexagons have (2×29 + 2 = 60) corners and (2×220 + 2 = 442) hexagonal yods, i.e., 221 hexagonal yods are associated with each hexagon. This is the number of hexagonal yods associated with each set of seven enfolded polygons that are outside the root edge (see Fig. 5). This demonstrates how the pair of joined hexagons embodies a property of the inner Tree of Life. There are 13 corners & centres of the nine tetractyses in each sector. The 248 yods therefore comprise (6×13=78) corners & centres (shown in Fig. 7 as green yods). They symbolise the 78 roots of E₆, an exceptional subgroup of E₈ that physicists have considered as a basis for the physics of the Standard Model (in other words, the currently known properties of subatomic particles). Six of the corners are centres of the sectors, leaving 72 other corners & centres. They correspond to the six simple roots of E₆ and its 72 other roots. There are 156 green yods in the two hexagons, where 156 is the 155th integer after 1 and 155 is the number value of ADONAI MELEKH, the Godname of Malkuth. As this Sephirah is the universe of physical matter, it is an indication that E₆ does, indeed, describe part of its physics.

5. Conclusion
The simple square symbolises the number 4, or Tetrad, so highly esteemed by the ancient Pythagoreans. The four integers 1, 2, 3 & 4 add up to 10, which is the number of Sephiroth of the Tree of Life and the number of points in the tetractys — an equivalent symbol of the ten-fold nature of divine unity and a representation of these integers. A square divided into tetractyses has 25 yods symbolising the 25 spatial dimensions of the universe. A square with each sector divided into three tetractyses has 60 yods surrounding its centre that correspond to the 60 extra yods making up the triangles of the Tree of Life when they are turned into tetractyses. A square with each sector divided into three triangles that are then divided into three tetractyses contains 168 yods surrounding its centre. This number characterises the manifestation of the Tree of Life in the subatomic world as the number of circularly polarised waves made by each one of the ten whorls of a spinning superstring as it completes half a revolution in space about its axis of spin, that is, one-tenth of the five complete revolutions of each whorl . The number 168 is defined arithmetically by a square because it is the sum of the twelve, successive odd integers after 1 that can be spaced along the sides of a square, four to each side. A square with each sector turned into the next higher-order tetractys above the tetractys contains 248 yods other than corners of tetractyses. These yods, which symbolise the seven Sephiroth of Construction, signify the 248 quantum states of the particle transmitting the unified force acting between superstrings of either ordinary or shadow matter. A 4×4 square array of the squares of the first four odd integers has as its sum the number (496) of such states responsible for the interactions of superstrings of both kinds of matter. Successive transformations of the square generate numbers corresponding to ever more concrete realisations of the cosmic blueprint. The fourth of the regular polygons embodies the 248 gauge fields of the superstring symmetry group E₈, the pair of these polygons embodying the dimension 496 of E₈×E₈. Truly, one must agree with the Pythagoreans in their calling the number 4 “the greatest miracle” and “holding the key of Nature."

References
1. Phillips, Stephen M. Article 1: “The Pythagorean nature of superstring and bosonic string theories,” (WEB, PDF), p. 4.
2. Named after Father Marin Mersenne, a natural philosopher, theologian, mathematician, musical theorist and friend of René Descartes, the nth Mersenne number is of the form M_n = 2ⁿ – 1, where n is an integer.
3. J. Adams, The Republic of Plato, Cambridge University Press, Cambridge, 1929.
4. Proof: Of the 264 yods in the seven enfolded polygons, 36 are corners of polygons and five more are just their centres. There are (264–36–5=223) hexagonal yods. Two of them lie on the root edge and 221 are external. Number of hexagonal yods in the (7+7) enfolded polygons = 2 + 2×221 = 444.

14