| << Previous 1... 40 41 [42] 43 44 ...56 Next >> |
#42 How some sacred geometries embody the 84:84 division in
the superstring structural parameter 168

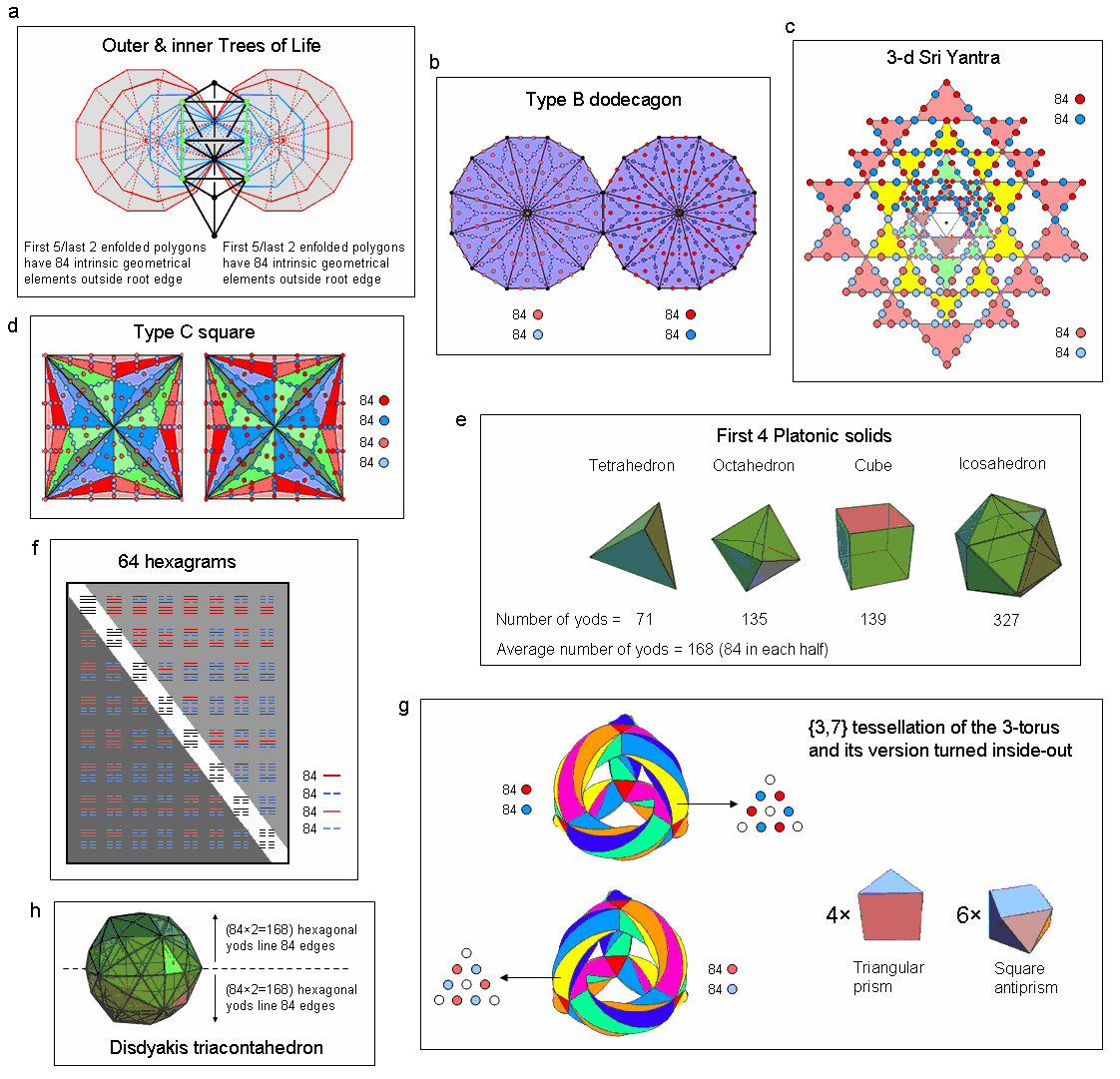
a) When the outer Tree of Life is superposed over the two sets of seven enfolded polygons in its inner form, three
corners and two sides of polygons in the latter coincide with corners & sides of triangles making up the former
(they are indicated in the diagram by green points & lines). Outside their shared root edge, the seven regular
n-gons making up each half of the inner Tree of Life have the following geometrical composition that is unshared
with the outer Tree of Life:
|
n = |
3 | 4 | 5 | 6 | 8 | 10 | 12 | Total |
| Corners | 1 | 3 | 3 | 2 | 7 | 9 | 11 | 36 |
| Sides | 5 | 7 | 9 | 7 | 15 | 19 | 23 | 85 |
| Triangles | 3 | 4 | 5 | 5 | 8 | 10 | 12 | 47 |
| Total | 9 | 14 |
17 |
14 |
30 | 38 | 46 | 168 |
| 84 | 84 | |||||||
| 168 | ||||||||
(The right-hand corner of the pentagon, which is also the centre of the decagon, will be associated with the latter). The table indicates that 168 corners, sides & triangles are intrinsic to the seven enfolded polygons, the first five polygons (coloured blue in the diagram) having 84 geometrical elements, as do the last two polygons (coloured red). A unique combination of polygons generates the gematria numbers of Cholem (78) and Yesodoth (90) adding to 168, namely, the triangle, pentagon, hexagon & decagon have 78 unshared geometrical elements and the square, octagon & dodecagon have 90 unshared geometrical elements;
b) A Type B dodecagon contains 181 yods. Two joined Type B dodecagons contain (181+177=358) yods. Of these, 22 yods are their corners (shown in the diagram by black yods), leaving 336 yods. 168 yods (including its centre) are associated with each dodecagon. Per sector of a separate dodecagon, there are seven hexagonal yods (dark red in one dodecagon, light red in the other) either on the sides of the sector or at the centres of the three tetractyses. There are also seven yods (dark blue or light blue) on the sides of these tetractyses. Each separate dodecagon has two sets of seven yods per sector that surround its centre. When joined, there are two sets of seven yods per sector, but, now, each sector sharing the same side includes the centre of the dodecagon instead of one of the two hexagonal yods on this side. The 168 yods associated with each dodecagon comprise 12 sets of seven red yods (dark or light) and 12 sets of seven blue yods (dark or light), i.e., they divide into two sets of 84 yods;
c) When the 42 triangles surrounding the central triangle of the 3-dimensional Sri Yantra are tetractyses, there are eight yods per tetractys, so that (42×8=336) yods line the (42×3=126) sides of the 42 tetractyses. 168 yods lie on the boundary of each half of the Sri Yantra. The six hexagonal yods on the three sides of each tetractys are the corners of two intersecting triangles that form a distorted Star of David. The corners of one triangle are red yods (light in one half of the Sri Yantra, dark in the other half) and the corners of the other triangle are blue yods (light or dark). There are four layers of eight, 10, 10 & 14 triangles. The yods at the outward-pointing tips of tetractyses are dark red or light red, those that lie directly above the blue yods at corners shared by adjacent triangles in the next lower layer being denoted as red circles. The eight yods per tetractys that line its sides consist of four red yods and four blue yods. The 21 tetractyses in each half of the Sri Yantra consist of (21×4=84) red yods and 84 blue yods. The 336 yods lining the 3-dimensional Sri Yantra consist of two sets of 168 yods, each set comprising two sets of 84 yods;
d) A Type C square is a square whose sectors are Type B triangles. It has 168 yods surrounding its centre. 21 red yods per sector either line the sides of the sectors of each Type B triangle or are at the centres of tetractyses. Seven blue yods line the sides of the three tetractyses making up each sector of a Type B triangle, so that there are (3×7=21) such yods per sector of the square. The 168 yods surrounding the centre of the Type C square consist of (4×21=84) red yods and 84 blue yods. (168+168=336) yods surround the centres of two separate Type C squares. They consist of 84 dark red yods, 84 dark blue yods, 84 light red yods & 84 light blue yods. This property of a Type C square, namely, that it has 168 yods surrounding its centre that divide naturally into two sets of 84 yods is an illustration of the Tetrad Principle governing holistic systems, for the Type C square is the fourth in the following sequence of types of squares, this type of regular polygon symbolizing the Tetrad (4):
square → Type A square → Type B square → Type C square →
Another illustration was provided in #16, where it was shown that the Type C version of the fourth type of regular polygon — the hexagon — embodies the dimension 248 of E8, the rank-8 Lie group describing the symmetry of the forces between one of the two types of heterotic superstring;
e) According to Table 1 on page 6 of Article 3, when the faces of the first four Platonic solids are divided into their sectors, each sector turned into a tetractys and each edge regarded as the side of an internal tetractys with the centre of the polyhedron as a corner, the yod populations of the tetrahedron, octahedron, cube & icosahedron are, respectively, 71, 135, 139 & 327. The total number of yods needed to construct them from tetractyses is 672. The average number of yods needed to construct them is 168. This is one way in which the four Platonic solids regarded by the ancient Greeks as the shapes of particles of the Elements, Fire, Air, Earth & Water embody the superstring structural parameter 168;
f) The 8×8 square array of 64 hexagrams forming the basis of the ancient Chinese system of divination called "I Ching" consist of eight diagonal hexagrams (coloured black) and 28 hexagrams in each diagonal half. A hexagram is a six-fold combination of unbroken lines (Yang) and broken lines (Yin). The former are coloured red (dark in the upper half of the array, light in its lower half) and the latter are coloured blue (dark in its upper half, light in its lower half). The (6×28=168) lines & broken lines in the 28 off-diagonal hexagrams in the upper half comprise 84 dark red lines and 84 dark blue broken lines. The lower half comprises 84 light red lines and 84 light blue broken lines;
g) A 3-torus can be modelled by four triangular prisms and six square antiprisms (see Article 43). When their 56 deformed, triangular faces are each represented by tetractys arrays of 10 yods, 168 hexagonal yods line their sides. The six hexagonal yods on the three sides of a tetractys are the corners of two intersecting triangles (Star of David). If the hexagonal yods at the corners of one triangle are coloured dark red and the hexagonal yods at the corners of the other triangle are coloured dark blue, the 168 hexagonal yods consist of 84 dark red hexagonal yods and 84 dark blue hexagonal yods.
|
|
3-torus turning inside out |
Turned inside-out, the 3-torus modelled from prisms and antiprisms have 168 hexagonal yods lining its 56 deformed tetractyses that consist of 84 light red hexagonal yods and 84 light blue hexagonal yods. Tessellated from 112 tetractyses, the 3-torus and its version turned inside-out have (168+168=336) hexagonal yods lining tetractyses, each set of 168 hexagonal yods comprising two sets of 84 hexagonal yods. As proved in #25, the 168 hexagonal yods lining the 56 tetractyses in the 3-torus denote the 168 roots of E8 that are not roots of its exceptional subgroup E6, whilst the 168 hexagonal yods lining tetractyses in the turned inside-out 3-torus denote the 168 roots of the second group E8 that are not roots of its subgroup E6;
h) The disdyakis triacontahedron (the Catalan solid with the most faces) has 62 vertices, 180 edges and 120 triangular faces. There are three types of vertices: A, B & C (see here). When orientated so that an axis passing through two diametrically opposite A vertices is vertical, the disdyakis triacontahedron has an equatorial plane containing 12 vertices that form the corners of a 12-gon (see here). (180−12=168) edges are above and below this plane, 84 in each half. When each triangular face is a tetractys, there are two hexagonal yods on each edge (84×2=168) hexagonal yods line the 84 edges above the equatorial plane and (84×2=168) hexagonal yods line the 84 edges below it. Constructed from tetractyses, the shape of the polyhedron is determined by 336 hexagonal yods, of which 168 hexagonal yods as 84 pairs lie above the equatorial plane perpendicular to the axis and 168 hexagonal yods as 84 pairs lie below it. A further (12×2=24) hexagonal yods line the central 12-gon, making a total of (336+24=360=36×10) hexagonal yods that line the 180 edges of the polyhedron. This shows how ELOHA, the Godname of Geburah with number value 36, prescribes the form of the disdyakis triacontahedron.
| << Previous 1... 40 41 [42] 43 44 ...56 Next >> |