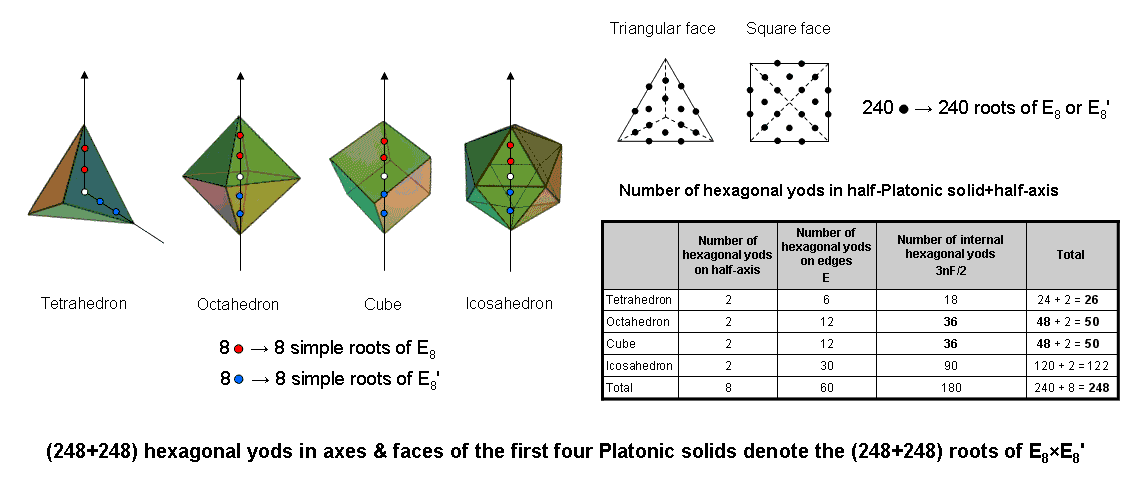
#39 The first four Platonic solids embody the 496 roots of E₈×E₈′

Suppose that a Platonic solid with E edges and F faces, each a regular n-gon with n sectors, is constructed from tetractyses. There are 2E hexagonal yods on its edges, 2nF hexagonal yods on the internal sides of the nF tetractyses and nF hexagonal yods at their centres, i.e., 3nF internal hexagonal yods. Suppose also that its edges are sides of internal triangles, each divided into three tetractys sectors. This means that each half of the Platonic solid has two red or blue hexagonal yods on the axis drawn through two opposite vertices and the white centre of the polyhedron (see diagram opposite). The table lists the numbers of hexagonal yods on and inside the edges of the tetrahedron, octahedron, cube & icosahedron. The number "2" refers to the two red or blue hexagonal yods on the axis in their upper or lower halves. The first four Platonic solids have eight hexagonal yods on their upper or lower half-axes and 480 hexagonal yods in their faces (240 black hexagonal yods in each half). Therefore, (248+248=496) hexagonal yods lie in their axes and faces. Each of the 248 hexagonal yods in the upper or lower halves of the first four Platonic solids denotes, respectively, a root of E₈ or E₈', the rank-8, exceptional Lie group with dimension 248. The eight red hexagonal yods on their axes in their upper halves symbolize the eight simple roots of E₈ and the eight blue hexagonal yods on their axes in their lower halves denote the eight simple roots of E₈′. The 240 black hexagonal yods in each set of halves denote the 240 roots of E₈ or E₈′:

The symmetry group of the E₈×E₈' heterotic superstring is embodied in the hexagonal yod population of the faces and axes of the first four Platonic solids.

The upper/lower halves of the tetrahedron and octahedron (or cube) have (24+48=72) hexagonal yods in their faces (see table). The upper/lower halves of the cube (or octahedron) and the icosahedron have (48+120=168) hexagonal yods in their faces. The number 72 is the number of roots of E₆, the rank-6 exceptional subgroup of E₈. Holistic systems embody the number 240 and always exhibit this 72:168 division, as demonstrated in many places on this website (see also the diagram above). For example, the 240 yods on the boundary of the two separate sets of seven enfolded polygons of the inner Tree of Life comprise their 72 corners and 168 hexagonal yods:

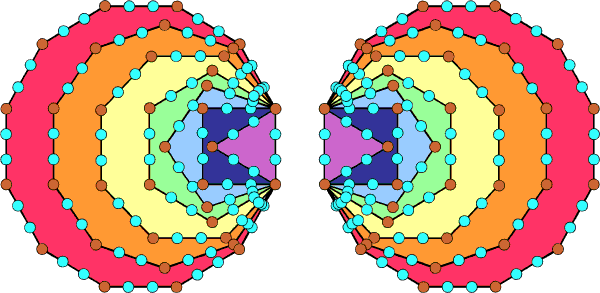
Notice that the faces of the tetrahedron, octahedron & cube have 120 hexagonal yods in each set of halves, as does the icosahedron. The 120:120 division of the number 240 is characteristic of holistic systems embodying this parameter. In the context of the first four Platonic solids, it differentiates not only the hexagonal yod populations of their halves but also the first three Platonic solids from the fourth one.

We now see that the belief of the ancient Greeks that the shapes of the first four Platonic solids determined the physics of the physical cosmos is correct, although not for the reason they supposed, namely, that particles of the Elements Fire, Air, Water & Earth have the shapes of these regular polyhedra. Instead, the yod composition of their faces and axes determine the root structure of E₈×E₈′, one of the two gauge symmetry groups governing the forces between heterotic superstrings. Although the second group SO(32) also has the dimension 496, its roots do not divide equally into two sets that mirror the two sets of halves of these Platonic solids. This is one of many reasons for believing that nature now favours E₈×E₈' over SO(32) as the gauge symmetry group governing superstrings. The direct product structure arises from the simple geometric fact that each yod in one half of a Platonic solid has a counterpart in its second half.

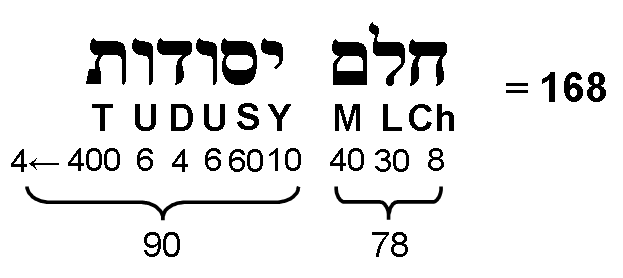
It is shown in Article 55 (p. 4) that the tetrahedron, octahedron, cube & icosahedron have 248 corners & sides of the 120 triangular sectors of the regular polygons in their faces. The 12 sectors of the four faces of the tetrahedron have eight corners, leaving 240 corners & sides. They comprise 72 corners & sides (the 60 corners of the octahedron, cube & icosahedron & 12 internal sides of the sectors of the tetrahedron) and 168 corners & sides (90 sides of the sectors in the icosahedron & 78 corners & sides in the tetrahedron, octahedron & cube). See Table 4 in Article 55. The number 78 is the number value of Cholem and the number 90 is the number value of Yesodoth, the two words making up the Kabbalistic name Cholem Yesodoth for the Mundane Chakra of Malkuth:

The embodiment of the number 248 in the geometrical composition of the faces of the first four Platonic solids is discussed here. The number of corners and sides of the n sectors in each of the F faces of a Platonic solid with C vertices = C + F + E + nF. Using the Euler polyhedral formula:

C − E + F = 2,

this simplifies to 2 + 2E + nF. "2" denotes the two vertices that lie on its axis, so that (2E+nF) corners & sides surround the axis. The first four Platonic solids have 240 corners & sides surrounding the axes that pass through eight vertices. This compares with the 240 hexagonal yods in the faces in each set of halves that surround the eight hexagonal yods in each set of their half-axes. So their geometry embodies the dimension 248 of E₈ and their hexagonal yod composition embodies the dimension 496 of E₈×E₈'. Here is remarkable evidence for how these Platonic solids, thought by the ancient Greeks to represent the shapes of the particles of the Elements Earth, Water, Air & Fire, embody the unified force between E₈×E₈' heterotic superstrings. How they embody the space-time structure of their subquark states is discussed here.

<< Previous    1...   37  38  [39]  40  41  ...56    Next >>

Home