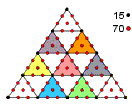
The 2nd-order tetractys
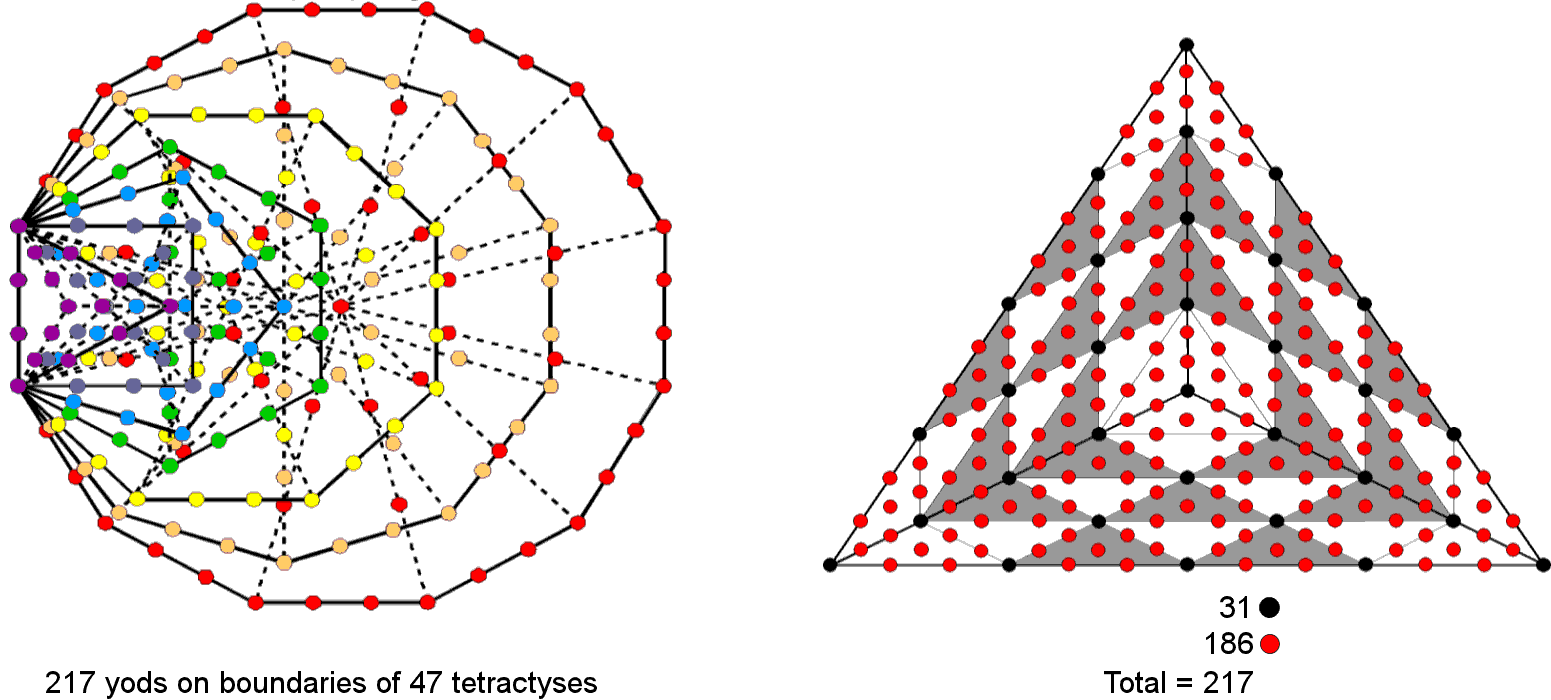
The triangle with 2nd-order tetractyses as its sectors embodies the number of yods lining the 47 1st-order tetractyses in the 7 enfolded, Type A polygons.
| << Previous 1... 72 73 [74] 75 76 ...81 Next >> |
#74 Correspondence between the inner Tree of Life and the triangle with 2nd-order tetractyses as its sectors
The 2nd-order tetractys contains 85 yods (15 corners & 70 hexagonal yods of 10 1st-order tetractyses). When the n sectors of an n-gon are 2nd-order tetractyses, the number of yods in the n-gon = 72n + 1, where "1" denotes the centre of the n-gon. The number of corners of the 10n 1st-order tetractyses = 10n + 1 and the number of hexagonal yods = 62n. The number 72 is the number of Chesed and 62 is the number of Tzadkiel, its Archangel. A triangle (3-gon) has 217 yods (216 yods surrounding its centre), of which 31 are corners of 30 1st-order tetractyses and 186 are hexagonal yods, where 31 is the number of EL, the Godname of Chesed.
Compare this with the seven enfolded, Type A polygons of the inner Tree of Life. They have 264 yods distributed in 47 tetractys sectors. Therefore, (264−47=217) yods line their sides. Of these, one yod is the topmost corner of the hexagon, which coincides with the lowest corner of the hexagon enfolded in the next higher, overlapping Tree of Life, leaving 216 boundary yods that are intrinsic to the set of seven polygons enfolded in each Tree, where 216 is the number of Geburah. The triangle with 2nd-order tetractyses as its sectors embodies the number of yods that shape the 47 tetractyses making up the seven enfolded polygons:
|
The 2nd-order tetractys |
 |
|
The triangle with 2nd-order tetractyses as its sectors embodies the number of yods lining the 47 1st-order tetractyses in the 7 enfolded, Type A polygons. |
There are 36 yods (12 black corners & 24 red hexagonal yods) on the sides of the triangle, where 36 is the number of ELOHA, the Godname of Geburah. 36 yods (12 corners & 24 hexagonal yods) line the sides of the dodecagon, whilst the seven enfolded polygons have 36 corners (12 corners of the dodecagon & 24 corners of the first six enfolded polygons). Because the dodecagon is holistic in itself, these two 12:24 patterns are counterparts of each other. The 36 corners of the seven enfolded polygons include: 1. the two endpoints of their root edge, 2. the right-hand corner of the triangle, which coincides with Chesed of the outer Tree, and 3. the top and bottom of the hexagon, which coincide with, respectively, Chokmah and Netzach. There are, therefore, 31 corners outside the root edge that are intrinsic to the inner Tree of Life. They correspond to the 31 corners of the 30 1st-order tetractyses in the triangle whose sectors are 2nd-order tetractyses.
Transformed by the 2nd-order tetractys, the simplest geometrical shape — the triangle — embodies the very number of yods needed to divide the seven enfolded polygons of the inner Tree of Life into their sectors. It is the seed that grows and flowers into the complete form of the inner Tree of Life.
The number 216 of Geburah is both the number of yods surrounding the centre of a triangle whose sectors are 2nd-order tetractyses and the number of yods lining the 88 sides of the 47 tetractyses in a set of seven enfolded polygons that are intrinsic to this set. As the four yods in the root edge are shared between both sets of polygons, there are (216−2=214) boundary yods associated with each set of polygons enfolded in successive Trees of Life. This is the number of yods in the outer form of the Tree of Life when its 16 triangles are Type A:
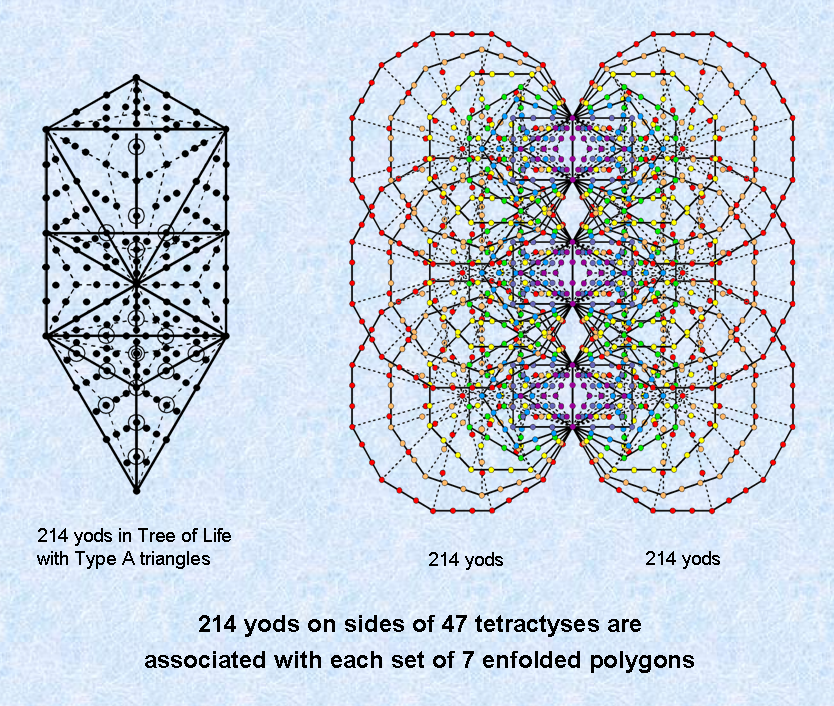
Given a triangle with its three corners, (217−3=214) more yods are needed to construct it from 2nd-order tetractyses. Embodied in the simple triangle and revealed by the 2nd-order tetractys is the very number of yods needed to construct from 1st-order tetractyses both the outer form of the Tree of Life and the inner form of every overlapping Tree of Life.
| << Previous 1... 72 73 [74] 75 76 ...81 Next >> |