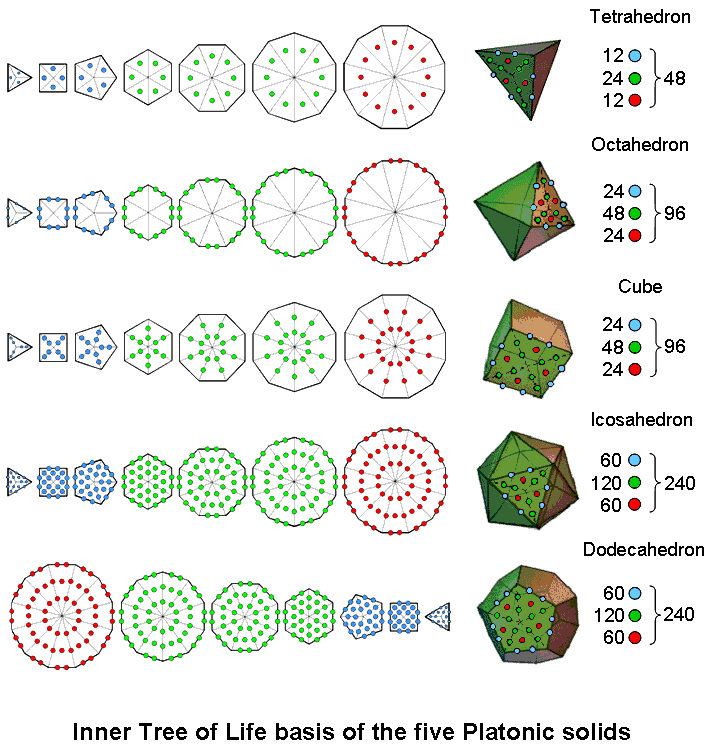
#57 Correspondence between the inner Tree of Life and the five Platonic solids

The seven separate regular polygons of the inner Tree of Life have 48 sectors, where 48 is the number value of Kokab, the Mundane Chakra of Hod. The first three polygons have 12 sectors, the next three polygons have 24 sectors and the last polygon (dodecagon) has 12 sectors.

Tetrahedron
The tetrahedron is the simplest Platonic solids. When the 12 sectors in its four faces are tetractyses, they have 48 hexagonal yods. They consist of:

• 12 blue hexagonal yods on its six edges ↔ 12 blue hexagonal yods at centres of sectors of the first three polygons;
• 24 green hexagonal yods on sides of tetractyses ↔ 24 green hexagonal yods at centres of sectors of the next three polygons;
• 12 red hexagonal yods at centres of tetractyses ↔ 12 red hexagonal yods at centres of sectors in the dodecagon.

Octahedron
When the 24 sectors in its eight faces are tetractyses, they have 96 hexagonal yods. They consist of:

• 24 blue hexagonal yods on its 12 edges ↔ 24 blue hexagonal yods on the sides of the first three polygons;
• 48 green hexagonal yods on sides of tetractyses ↔ 48 green hexagonal yods on sides of the next three polygons;
• 24 red hexagonal yods at centres of tetractyses ↔ 24 red hexagonal yods on sides of the dodecagon.

Cube
When the 24 sectors in its six faces are tetractyses, they have 96 hexagonal yods. They consist of:

• 24 blue hexagonal yods on its 12 edges ↔ 24 blue hexagonal yods on internal sides of tetractyses in the first three polygons;
• 48 green hexagonal yods on sides of tetractyses ↔ 48 green hexagonal yods on internal sides of tetractyses in the next three polygons;
• 24 red hexagonal yods at centres of tetractyses ↔ 24 red hexagonal yods on internal sides of tetractyses in the dodecagon.

Icosahedron
When the 60 sectors in its 20 faces are tetractyses, they have 240 hexagonal yods. They consist of:

• 60 blue hexagonal yods on its 30 edges ↔ 60 blue hexagonal yods in the first three polygons;
• 120 green hexagonal yods on sides of tetractyses ↔ 120 green hexagonal yods in the next three polygons;
• 60 red hexagonal yods at centres of tetractyses ↔ 60 red hexagonal yods in the dodecagon.

Dodecahedron
When the 60 sectors in its 12 faces are tetractyses, they have 240 hexagonal yods. They consist of:

• 60 blue hexagonal yods on its 30 edges ↔ 60 blue hexagonal yods in the first three polygons of the mirror-image set of seven polygons making up the second half of the inner Tree of Life;
• 120 green hexagonal yods on sides of tetractyses ↔ 120 green hexagonal yods in the next three polygons of the mirror-image set;
• 60 red hexagonal yods at centres of tetractyses ↔ 60 red hexagonal yods in the dodecagon of the mirror-image set.

As the fourth Platonic solid, the icosahedron represents the completion of the archetypal sequence of generation of the regular polyhedra, starting with the tetrahedron. Not only does it have the same number of hexagonal yods as the seven separate polygons of the inner Tree of Life do but also the 60:120:60 pattern of their spatial distribution is the same as that shown by the 3:3:1 pattern of polygons constituting each half of the inner Tree of Life. Its dual — the dodecahedron — contains the same number of hexagonal yods as there are in the second set of seven polygons in the mirror-image half of the inner Tree of Life. The duality of these two regular polyhedra is the three-dimensional counterpart of mirror reflection of the seven polygons. The five Platonic solids are sacred because they are the regular polyhedral counterpart of the sacred geometry of the inner Tree of Life. As many other pages in this website point out, the scientific meaning of the 240:240 division of hexagonal yods between either the first three Platonic solids and the fourth one or between the fourth and fifth ones is that they embody the (240+240) roots of E₈×E₈, one of the two Lie groups that were discovered in 1984 by physicists Michael Green and Gary Schwarz to govern superstring interactions that are free of quantum anomalies. The embodiment is discussed here and here.

<< Previous    1...   55  56  [57]  58  59  ...81    Next >>

Home