| << Previous 1... 44 45 [46] 47 48 ...81 Next >> |
#46 Correspondences between the tetrahedron and the outer & inner Trees of Life
We saw in #44 that the number 85 is the number of intrinsic corners of the 141 triangles in the seven enfolded Type B polygons making up each half of the inner Tree of Life. We now show how this number and other parameters of holistic systems are embodied in the geometry of the tetrahedron — the embryonic form for the sacred geometry of the Platonic solids.
When its faces and internal triangles are simple triangles, the tetrahedron has 24 geometrical elements surrounding its centre:
| Corners | Sides | Triangles |
Total |
|
| Faces: | 4 | 6 | 4 | 14 |
| Interior: | 1 | 4 | 6 | 11 |
| Total | 5 | 10 | 10 | 25 |
As a symbol for the number 4 (the Pythagorean Tetrad), it is appropriate that the tetrahedron consists of this number of geometrical elements, for 24 = 4! = 1×2×3×4, i.e., the number of permutations of four objects. The square is another symbol of the number 4. When its sectors are tetractyses, it consists of 25 yods, 24 of which surround its centre (see here).
Type A triangles
When its faces and internal triangles are Type A triangles, the
tetrahedron has 85 geometrical elements ("+1" refers to its centre):
| Corners | Sides | Triangles |
Total |
|
| Faces: | 8 | 18 | 12 | 38 |
| Interior: | 6+1 | 22 | 18 | 46+1 |
| Total | 14+1 | 40 | 30 | 84+1 |
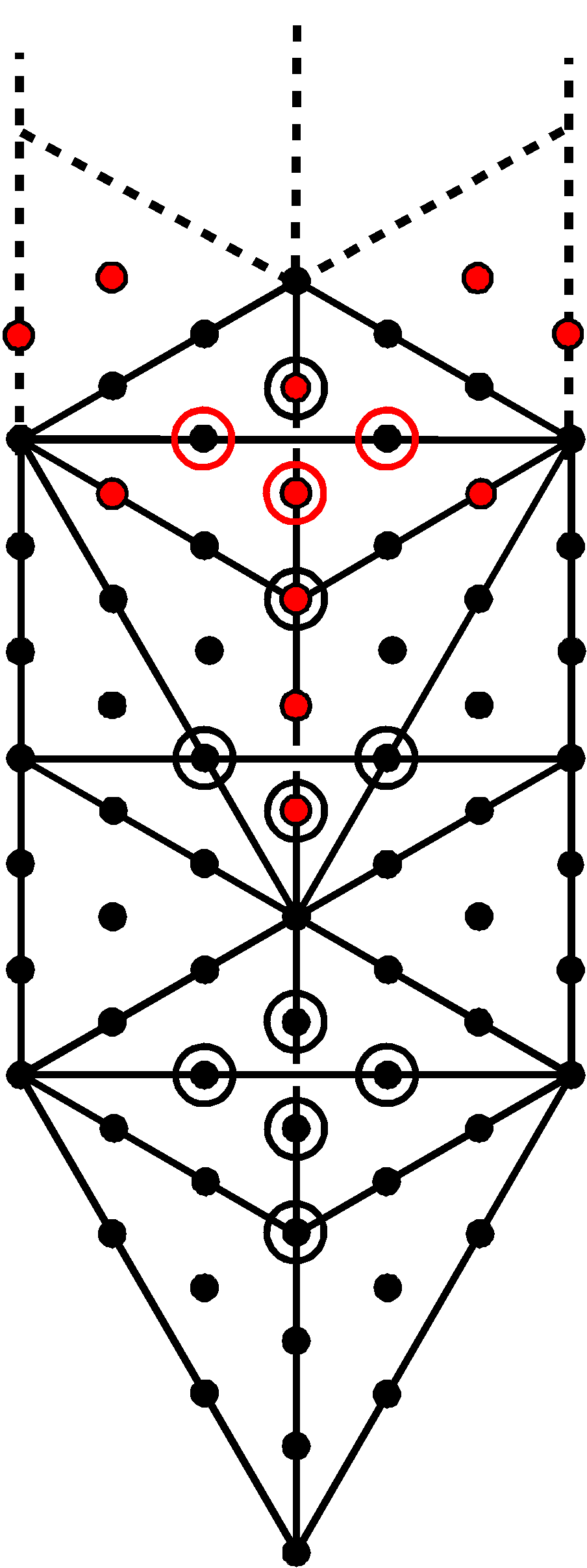
This is the number of yods in a 2nd-order tetractys (see here). As the latter is a representation of holistic systems, it shows that the tetrahedron has a holistic character, albeit in embryonic form. The 15 corners and the (40+30=70) sides & triangles correspond, respectively, to the 15 corners of the ten 1st-order tetractyses and to their 70 hexagonal yods. 84 geometrical elements surround its centre, where 84 = 12 + 32 + 52 + 72. An axis passing through two vertices and the centre of the tetrahedron is made up of three points and two straight lines. Surrounding it are 80 geometrical elements (12 corners, 38 sides, 30 triangles). They consist of 50 corners & sides and 30 triangles. Compare these properties with the 1-tree:

The 1-tree
With its 16 triangles turned into tetractyses, the Tree of Life has 70 black yods. They correspond to the 70 sides & triangles in the faces and interior of the tetrahedron. Ten red yods are added by its conversion into the 1-tree and four red hexagonal yods are outside the 1-tree up to the level of its apex. The former correspond to the 10 corners of the sectors in the faces and internal triangles and the latter correspond to the two vertices and the two sides making up the axis. The 80 yods in the 1-tree symbolize the 80 geometrical elements that surround the axis of the tetrahedron. Their counterparts in the inner Tree of Life are the 80 corners of the 94 sectors of the (7+7) enfolded Type A polygons, which comprise the 70 corners of polygons and their ten centres that are not corners (see here). The 10:70 division that exists in both the 1-tree and the inner Tree of Life manifests in the tetrahedron because it is their polyhedral counterpart. The 50:30 division of its geometrical elements corresponds in the 1-tree to the 50 yods outside the Lower Face and to the 30 yods in the latter.
Type B triangles
When its faces and internal triangles are Type B triangles, the
tetrahedron has 264 geometrical elements surrounding its centre:
| Corners | Sides |
Triangles |
Total |
|
| Faces: | 20 | 54 | 36 | 110 |
| Interior: | 24+1 | 76 | 54 | 154+1 |
| Total | 44+1 | 130 | 90 | 264+1 |
They comprise 44 corners, 130 sides & 90 triangles. 36 triangles are in the faces and 54 are internal. This conforms to the archetypal pattern of the 10 integers in the Lambda Tetractys, the sum of the integers at its corners being 36 and the sum of its seven remaining integers being 54 (see here). Furthermore, in a remarkable confirmation of the holistic status of the tetrahedron, its 264 geometrical elements correspond to the 264 yods in the seven enfolded polygons of the inner Tree of Life when their 47 sectors are tetractyses:
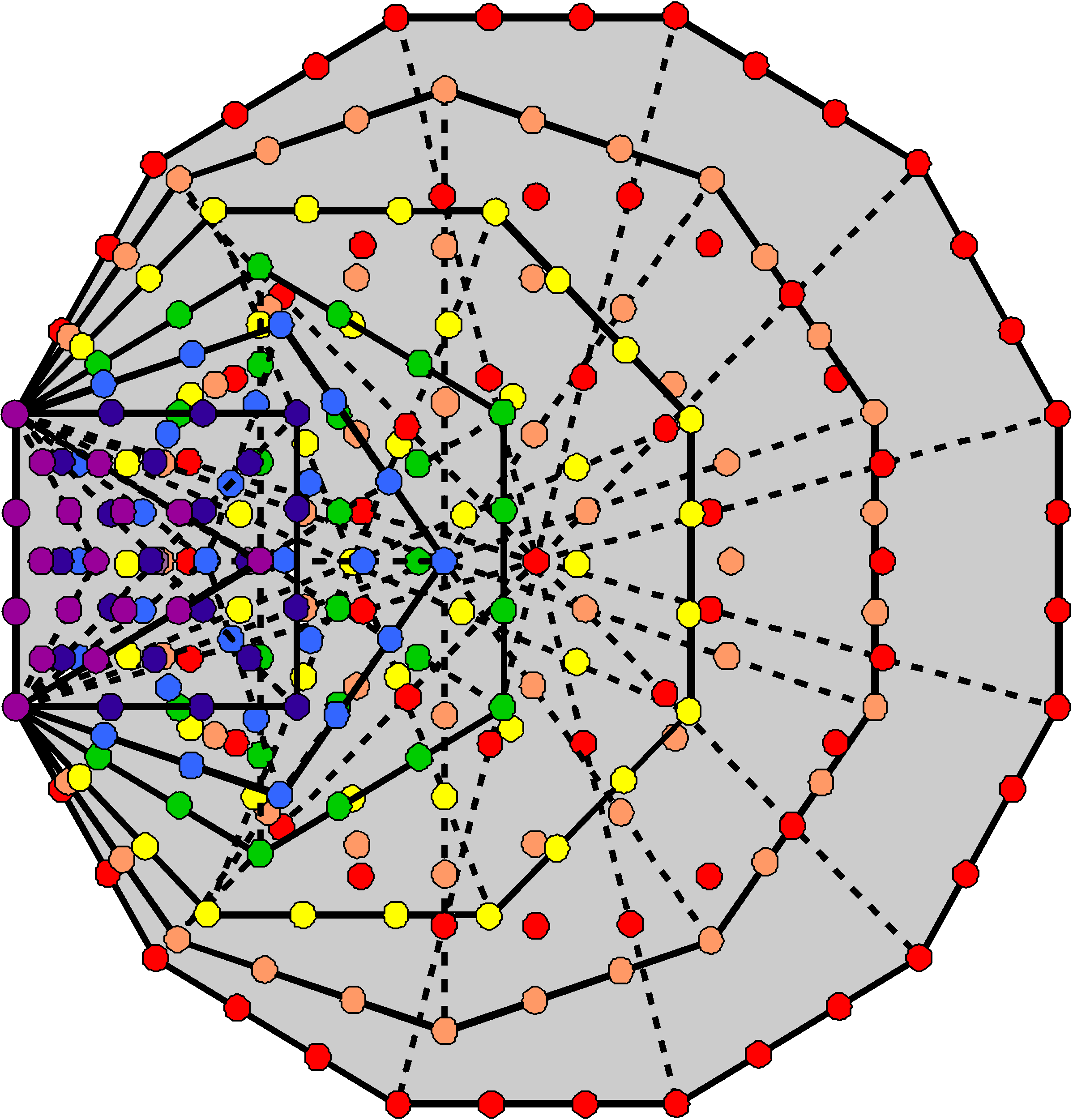 |
The 47 tetractyses making up the seven enfolded Type A polygons have 264 yods. |
The four yods in the root edge correspond to the four geometrical elements (two vertices, two sides) in the axis that surround the centre of the tetrahedron. Surrounding it are 260 (=26×10) geometrical elements, showing how YAHWEH, the Godname of Chokmah with number value 26, prescribes the Type B tetrahedron. Outside the root edge of the first four enfolded polygons — the triangle, square, pentagon & hexagon — are 90 yods, the numbers in each being the sums of the four sets of integers in the Lambda Tetractys (see here). They correspond to the 90 triangles, the 36 yods in the triangle & square corresponding to the sum of the first two sets of integers and to the 36 triangles in the faces of the tetrahedron, whilst the 54 yods in the pentagon & hexagon correspond to the sum of the third & fourth sets of integers and to the 54 internal triangles. The last three enfolded polygons have 170 yods outside the root edge that correspond to the 170 corners & sides surrounding the axis of the tetrahedron. The yod composition of the seven enfolded polygons is a representation of all holistic structures, such as the tetrahedron and the disdyakis triacontahedron. In this sense, it can be regarded as more fundamental than such polyhedral realizations.
YAHWEH ELOHIM, the Godname of Tiphareth with number value 76, prescribes the 76 internal sides of the 54 triangles in the interior of the tetrahedron. The table above indicates that, including the centre, there are 155 internal geometrical elements, where 155 is the number value of ADONAI MELEKH ("The Lord and King"), the complete Godname of Malkuth. They comprise:
| << Previous 1... 44 45 [46] 47 48 ...81 Next >> |