Home

 15.  The 8 triacontagons embody the global structural parameter of the UPA

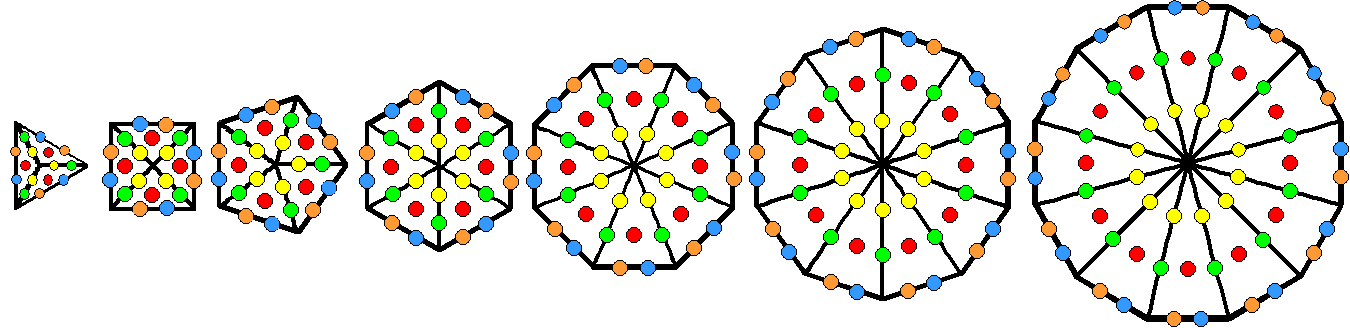
Constructed from 2nd-order tetractyses, the 8 triacontagons in the E8 Coxeter plane projection of the 421 polytope have 16800 yods other than polygonal corners surrounding the centres of their 240 sectors.

Consider an n-gon whose sectors are 2nd-order tetractyses. The number of yods other than sector corners that surround the centres of its n sectors = 70n (for proof, see details in the picture above). A triacontagon (n=30) has 2100 such yods. Eight concentric triacontagons have 16800 yods other than the 240 corners of their sectors. 8400 yods are in either set of 4 triacontagons whose corners are the 120 vertices of a 600-cell. The 4-d projection of the 4₂₁ polytope is a compound of two 600-cells whose 120 vertices are represented by a set of 4 triacontagons. The fact that the 8 triacontagons embody both the numbers 8400 and 16800 as structural parameters of the UPA is highly significant. It indicates that the 4₂₁ polytope not only represents the 240 roots of E₈ but also embodies the structural parameters of the fundamental constituents of matter first described with a form of remote-viewing by Annie Besant & C.W. Leadbeater 122 years ago and identified by the author as E₈×E₈ heterotic superstrings. Its outer and inner halves, each with 8400 turns in its 10 whorls, correspond to the pair of 600-cells, each corresponding to 4 red or blue triacontagons (see picture) with 8400 yods surrounding the centres of their 120 sectors. Just as the triacontagon has a 5-fold, rotational symmetry, so each whorl makes 5 complete revolutions about the axis of the UPA. The 3-dimensional form of the UPA, of course, does not exhibit 5-fold, rotational symmetry. But the 48 sectors in 1/5 of the complete set of 240 sectors have 3360 yods surrounding their centres — just as each of the 5 revolutions of the 10 whorls contains 3360 turns. Therefore, this correspondence could imply a connection between the two properties that is far more than an analogy. That this is the case is indicated by the way in which the inner form of the Tree of Life displays the factorisation:

240 = 5×48

 in the 240 hexagonal yods in its 7 separate regular polygons when transformed into 1st-order tetractyses. Their 48 sectors have 5 hexagonal yods per sector:

The 5 types of hexagonal yods are shown above in different colours. The correspondence is established below (underlined numbers denote numbers of sectors of polygons):

48 = 3 + 4 + 5 + 6 + 8 + 10 + 12

  = 3 + (4+8) + (5+10) + (6+12)

  = 3 + 4×(1+2) + 5×(1+2) + 6×(1+2)*

  = 3 + 4×3' + 5×3'' + 6×3''' ( 3 = sectors of triangle, 3' = sectors of square/octagon, 3'' = sectors of pentagon/decagon, 3''' = sectors of hexagon/dodecagon)

  = (3 + 5×3'') + 4×3' + 6×3'''

  = 6×3* + 2×2×3' + 6×3''' (3* = sectors of triangle/pentagon/decagon)

  = 6×3* + 6×2' + 6×3'''

  = (6×3* + 6×1') + (6×1' + 6×3''')

  = 6×(3*+1') + 6×(1'+3''')

  = 6×4 + 6×4' (4 = 3* + 1' = sectors of triangle/square/pentagon/octagon/decagon; 4' = 1' + 3''' = sectors of square/hexagon/octagon/dodecagon)

  = 6×8,

where 8 = 4 + 4'. Therefore,

240 = 5×48 = 5×6×8 = 30×8.

This means that the 240 hexagonal yods, which symbolise the 240 roots of E₈, can be regarded as two sets (120, 120') of 120 hexagonal yods, where:

120 = 5×6×4 and 120' = 5×6×4'.

Each set consists of 5 groups of 24 hexagonal yods, all the yods in a group being of the same colour. This is the inner Tree of Life counterpart of the 4₂₁ polytope as a compound of two 600-cells with 120 vertices, each 600-cell being a compound of five 24-cells with 24 vertices. Each set of 120 hexagonal yods corresponds to the 4 triacontagons in a 600-cell. The 30 vertices in a triacontagon consist of 6 sets of 5. Similarly, their counterpart hexagonal yods comprise 6 sets of 5 differently coloured hexagonal yods symbolising different Sephiroth of Construction. Every 6 successive corners of a triacontagon correspond to 6 hexagonal yods of the same colour. Because the seven polygons in the inner Tree of Life have 48 sectors containing 48 hexagonal yods of each colour, these sets of 6 hexagonal yods are repeated 8 times for the seven polygons. The 8 triacontagons are the counterpart of this 8-fold repetition.

An analogous 5×48 and 8×30 pattern are found in the geometrical composition of the 2-dimensional Sri Yantra and in other sacred geometries (see here). For example, surrounding an axis that passes through two diametrically opposite B vertices of the disdyakis triacontahedron are 240 vertices & edges that comprise 10 sets of:

three A vertices,
one B vertex,
two C vertices,
six AB edges,
six BC edges,
six CA edges.

Grouping together the single B vertex and the two C vertices, there are 30 sets of:

one A vertex,
one B or C vertex,
two AB edges,
two BC edges,
two CA edges,

i.e., 30 sets of 8 vertices & edges. Each set comprises two subsets of 4, a subset consisting of the 3 types of edges (AB, BC & CA) and a vertex (A, B or C). Alternatively, each half of the disdyakis triacontahedron has 30 sets of the three types of edges and one vertex, which is either A, B or C, so that the fact that every vertex and edge has its mirror image generates the same division: 8 = 4 + 4 as that in the 8 triacontagons. If we connect every vertex of the 120-faced polyhedron to its centre, its axis is surrounded by 30 sets of 8 sides of (120+180=300) triangles, i.e., 240 sides. This polyhedron is the only one among the Archimedean and Catalan solids whose axis is surrounded by 240 vertices & edges composed of 60 vertices and 180 edges, that is, two numbers that are both multiples of 30, thereby being the only polyhedron whose geometry allows a correspondence with the eight sets of 30 vertices of the triacontagons in the E₈ Coxeter plane projection of the 4₂₁ polytope (to verify this uniqueness, see the table here). The correspondence exists because, as shown in many pages of this website, the disdyakis triacontahedron is the polyhedral version of the universal blueprint embodied in sacred geometries whose polytopic form is the 4₂₁ polytope with the symmetries of the Lie group E₈ present in the theory of E₈×E₈ heterotic superstrings. The inner Tree of Life is its polygonal form. We have therefore revealed an analogous pattern in the polygonal, polyhedral and polytopic versions of this blueprint. We assert that the only plausible reason for this remarkable correlation is that E₈×E₈ heterotic superstrings exist.

<< Previous    1...   13  14  [15]  16  17    Next >>

Home