Mathematicians are familiar with a class of integers that they call "perfect numbers." These are positive integers whose divisors (including the trivial number 1 but excluding the perfect number itself) add up to themselves. The first perfect number is 6 because:

1 + 2 + 3 = 6,

where 1, 2 & 3 are its divisors. The second perfect number is 28 because:

1 + 2 + 3 + 4 + 5 + 6 + 7 = 28

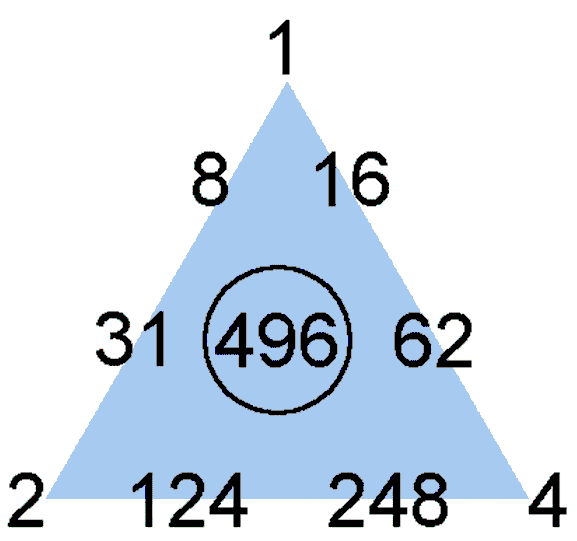
and 1, 2, 3, 4, 5, 6 & 7 are its divisors. The third perfect number is 496 because

1 + 2 + 4 + 8 + 16 + 31 + 62 + 124 + 248 = 496,

where 1, 2, 4, 8, 16, 31, 62, 124 & 248 are its nine divisors. This means that, if the number 496 is assigned to the centre of a tetractys, its nine divisors can be assigned to the nine yods that surround it. As the centre of a tetractys symbolizes Malkuth, the last Sephirah of the Tree of Life, whose gematria number value is 496 (see here), the tetractys pattern of this number is very apt!

The dimension of E₈×E₈ is 496. The dimension 248 of each Lie group E₈ is the sum of the first eight divisors of 496:

1 + 2 + 4 + 8 + 16 + 31 + 62 + 124 = 248.

As 31 = 2⁵ − 1, 62 = 2×31 = 2(2⁵ − 1) = 2⁶ – 2, and 124 = 2×62 = 2(2⁶ − 2) = 2⁷ – 4,

248 = 2³ + (2⁴ + 2⁵ + 2⁶ + 2⁷) = 8 + 240,

and

496 = 2×248 = 2⁴ + (2⁵ + 2⁶ + 2⁷ + 2⁸) = 16 + 480.

We see that the number 240 is the sum of four consecutive powers of 2, starting with the power 4:

240 = 2⁴ + 2⁵ + 2⁶ + 2⁷.

This demonstrates how the Pythagorean Tetrad (4) determines the number 240, which is a parameter of holistic systems, being:

1. the number of hexagonal yods in the seven regular polygons of the inner Tree of Life (see here);
2. the number of yods in the 1-tree other than its SLs (see here);
3. the number of hexagonal yods in the faces of either the first three Platonic solids, the icosahedron or the dodecahedron (see here);
4. the number of geometrical elements in the 2-dimensional Sri Yantra that surround its centre (see here).

The reason for this is that E₈ has 240 roots, each associated with a gauge charge and spin-1 field that transmits part of the superstring force. These roots are the counterparts of the yods or geometrical elements in these sacred geometries, thereby illustrating the holistic/sacred geometrical nature of the E₈×E₈ heterotic superstring, as opposed to the SO(32) heterotic superstring, whose symmetry group has 496 roots among which 240 roots are not differentiated.

<< Previous    1...   2  3  [4]  5  6  ...50    Next >>

Home