How the Golden Ratio determines the construction of the Sri Yantra

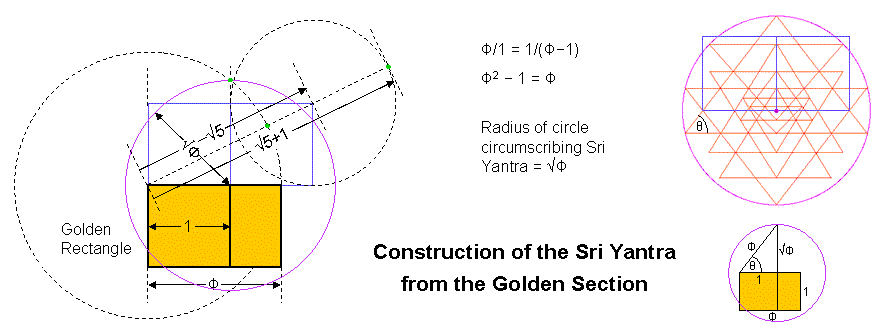
Artists and architects have know for a long time (how long remains a matter of controversy) that a certain rectangle has a particularly attractive appearance. It is know as the "Golden Rectangle." If the shorter side has length 1 in any unit of size, the longer side of this rectangle has the length Φ = (√5+1)/2, where Φ  =1.6180339887498948482... is called the "Golden Ratio."  A square drawn in the Golden Rectangle with its shorter side as one side divides its longer side in the proportion 1:(Φ−1). What is remarkable about this particular rectangle is that this ratio is equal to Φ. Any line segment divided according to this proportion is called the "Golden Section." Many books have been written about the role played by this number in nature and in human culture. The book by Dr Scott Olsen entitled "The Golden Section — Nature's Greatest Secret" is especially recommended. Rather than review material about the Golden Ratio that can be quickly found on the internet with search engines, it will be now shown how Φ, the "divine proportion," determines the form of the Sri Yantra.

Starting with a corner of the square within the Golden Rectangle, draw a circle of radius Φ (the black-dashed line on the left below). Extend upwards a vertical side of the square until it intersects the circle (denoted by one of the green dots). As Φ² – 1 = Φ, Pythagoras' theorem tells us that the length of the third side of the right-angled triangle with a base length of 1 and a hypotenuse of length Φ is √Φ (see below). The angle θ between the base and hypotenuse is 51°49′38″. Now draw a pink circle of radius √Φ with its centre at the right-angled corner of the triangle. The animation below demonstrates how a Sri Yantra circumscribed by this circle can be constructed from the Golden Section. 

The sides of the two largest triangles in the Sri Yantra are inclined to their horizontal bases by the angle θ. It is amazing that the faces of the Great Pyramid of Khufu are inclined to the horizontal by an angle of 51°50′40″ (see here), which differs from θ by only about one minute of arc! Because they have no evidence that the ancient Egyptians knew about the Golden Ratio, mainstream Egyptologists are obliged to regard such a close agreement as coincidence. It is still the general view amongst academics that the discovery of Φ must be attributed to Euclid (c. 325–c. 265 BCE), although their flimsy reason for thinking this is merely that he was the first to refer to it in his Elements (his famous treatise on geometry and number, written about 300 BCE). This, of course, does not prove that he was the first to analyze the mathematics of the Golden Ratio, nor does it indicate that knowledge of it was unknown to anyone before him. Perhaps it was never written down in the systematic way that made Euclid famous. Perhaps, before the time of Euclid, it was regarded as a deep secret that could not be disclosed in a book. The notion that the ancient Egyptians could have designed the largest structure ever built with an angle of inclination that simply by chance is only one minute of arc different from the angle θ is, frankly, so implausible as to be unbelievable, notwithstanding that it may be a respectable position to hold in the corridors of academia, in view of the absence of any reference to these mathematical ideas in surviving, ancient Egyptian records. But never underestimate the ability of evidence-based scholarship to fly sometimes in the face of common sense by denying the existence of things that lack the 'right' kind of evidence for them! Anyway, the long-held academic view that Euclid was the first to write about the Golden Ratio is plain wrong and needs to be corrected because Dr Scott Olson, Associate Professor of Philosophy & Comparative Religion at Central Florida Community College, proved beyond doubt in 2002 that Plato referred to it about 80 years earlier in his Republic (c. 380 BCE), albeit in a more enigmatic way.* Indeed, as Olsen has pointed out, Sir Thomas Heath, the distinguished historian of ancient Greek mathematics, stated** in his The Thirteen Books of Euclid's Elements that Plato and his students in the Academy worked on theorems about the Golden Ratio. Euclid was born about 22 years after Plato died. Given that Plato borrowed much of his mathematics from the Pythagoreans and that Pythagoras spent many years in Egypt, studying with its priests, it is highly plausible (indeed, probable) that — like so much of his wisdom — the latter learnt about the mathematics and philosophy of the Golden Ratio from his time in that country. This, of course, has to remain a speculation. However, only someone still conditioned by the long-held (but now discredited) belief in the West that ancient Greece was the birthplace of all science and mathematics could remain unconvinced by the astonishing closeness of the Great Pyamid's inclination angle to the angle θ. That the largest triangles of the Sri Yantra have the shape of the vertical cross section of the Great Pyramid is no less remarkable. For those unwilling to accept that the sacred geometries of religions share a fundamental, mathematical design sometimes expressed in their architectures, this has to be another coincidence. But those who cannot believe such improbable miracles have a more sensible explanation......

* Olsen, Scott A. "The Indefinite Dyad and the Golden Section: Uncovering Plato's Second Principle", Nexus Network Journal, vol. 4, no. 1 (Winter 2002), http://www.nexusjournal.com/GA-v4n1-Olsen.html

** Heath, Thomas L. 1956. The Thirteen Books of Euclid's Elements (3 vols. 2nd ed. 1926. Rpt. New York: Dover Publications), vol.1, 137.

<< Previous    1...   4  5  6  [7]  8    Next >>

Home