| << Previous 1 [2] Next >> |

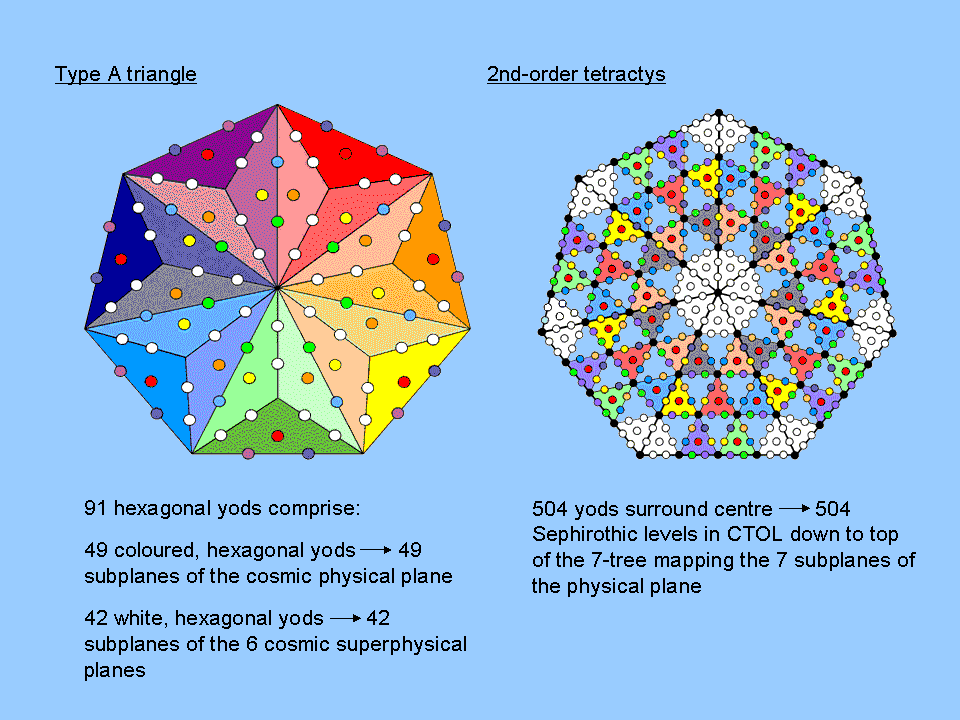
Heptagon with Type A triangles as sectors
A symbol of the seven-fold nature of Man and the seven Sephiroth of the spiritual cosmos, the heptagon has 91
hexagonal yods when its sectors are Type A triangles. Each denotes one of the subplanes of the seven cosmic planes
of consciousness and one of the Trees of Life in CTOL. The 49 coloured, hexagonal yods either
at the centres of tetractyses or lining their sides denote the 49 Trees of the
49-tree that maps the cosmic physical plane; the 42 white hexagonal yods on sides of tetractyses
inside each sector of the heptagon denote the 42 Trees of Life above the 49-tree that map the 42
subplanes of the six cosmic superphysical planes. This is the single, polygonal representation of
CTOL.
Heptagon with 2nd-order tetractyses as sectors
When its sectors become 2nd-order tetractyses, the 504 yods surrounding the centre of the heptagon denote the 504
SLs down to the top of the 7-tree, which is represented by its central yod. They are the counterpart of the 504
hexagonal yods that line the 126 tetractyses making up the 42 triangles of the Sri Yantra. Notice that there are 84
yods on the boundary of the heptagon. As they shape the polygons, it makes sense, intuitively
speaking, to regard them as corresponding to the 84 dark green SLs on the central pillar between the top of the
49-tree and the top of the 7-tree, for they belong to the Tree of Life map of the cosmic
physical plane. The 7-tree is the 'Malkuth' level of the 49-tree, which in turn is
the 'Malkuth' level of CTOL — the most general sense of this word. The top of the 7-tree is the
168th SL on the Pillar of Equilibrium from the top of CTOL, where 168 is the
number of Cholem Yesodoth, the Mundane Chakra of Malkuth (see the diagram on the previous
page depicting the correspondence between CTOL and the Sri Yantra). This is amazing evidence of how the
gematria number values of the Sephiroth in the four Kabbalistic Worlds of Atziluth, Beriah, Yetzirah & Assiyah
quantify their properties as manifested in each World. The superstring structural
parameter 168 discovered by C.W. Leadbeater over a hundred years ago in his micro-psi
examination of the UPA actually marks out the physical universe (7-tree) from all superphysical levels of
reality (84 higher Trees). That cannot be due to chance! Here, therefore, are
two undeniable pieces of mathematical evidence that confirm his paranormal discovery: firstly, the gematria number
value of the Mundane Chakra of Malkuth is 168, and, secondly, there are 168 SLs
on the Pillar of Equilibrium down to the Malkuth level of CTOL, namely, space-time.
The ancients believed that the Earth was the centre of the universe — or so we now interpret their beliefs. A deeper idea lies behind their regarding our planet as the centre of physical reality. It is that Earth symbolized the plane of physical awareness that is the centre, or fulcrum, of the spiritual cosmos (CTOL), which is encoded in the inner Tree of Life (see here) and represented by the Sri Yantra. In the Kabbalistic, astrological correspondence between Sephiroth and astronomical bodies, the planet Earth is assigned to Malkuth at the bottom of the Tree. It represents the Element Earth — the substance of the physical universe, which includes both ordinary matter and yet to be detected dark matter.
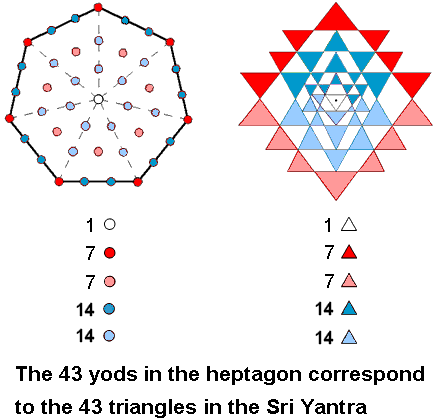
We saw on the previous page that the 3-dimensional Sri Yantra is equivalent to CTOL in that the 550 yods on the boundaries of the 126 tetractyses in its 42 Type A triangles and in its central, Type B triangle denote the 550 SLs in CTOL. The Type A heptagon has 42 yods surrounding its central yod. They correspond to the 42 triangles surround the central triangle in the Sri Yantra:
The number of yods in the Type C n-gon = 42n + 1. The Type C heptagon (n=7) has 295 yods. This is the number of yods in the seven separate Type A polygons of the inner Tree of Life:
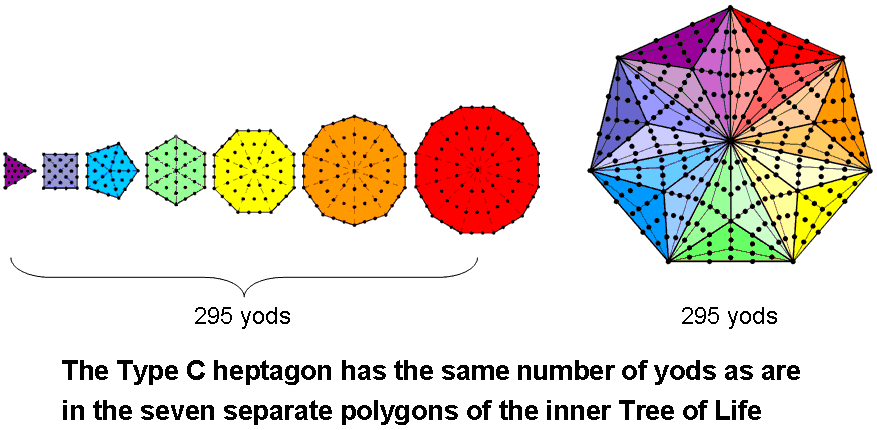
This is also the number of SLs up to Chesed of the 49th Tree of Life in CTOL. In other words, this number measures the number of SLs in CTOL up to the first Sephirah of Construction of the Tree of Life that maps the highest of the 49 subplanes of the cosmic physical plane and which represents the same Sephirah, the first subplane of the Adi plane corresponding to Chesed. The seven centres of the polygons, or the seven corners of the heptagon, are the counterpart of the lowest seven SLs of the 1-tree and the 288 remaining yods in either case are the counterpart of the next 288 SLs up to Chesed of the 49th Tree, where
288 = 11 + 22 + 33 + 44
| 10 | |||||||
| 21 | 21 | ||||||
| = | 32 | 32 | 32 | ||||
| 43 | 43 | 43 | 43 |
As 248 + 47 = 295, there are 248 SLs up to Chesed of the 49th Tree beyond the 47th SL, which is both the top of the 7-tree and the 168th SL on the Pillar of Equilibrium from the top of CTOL. This connects the superstring structural parameter 168 at the core of Leadbeater's micro-psi observations to the dimension 248 of E8, the rank-8, exceptional Lie group describing E8×E8 heterotic superstrings. The significance of this remarkable relationship generated by the geometry of CTOL hardly needs to be emphasized. It mathematically connects the number (1680) of circular turns in each helical whorl of the UPA/subquark superstring remote-viewed by Besant & Leadbeater to the dimension of the very Lie group predicted by superstring theory to govern the forces between one of the five types of superstrings, just as we found on the previous page that the same number is connected to the dimension 496 of the two types of symmetry groups describing superstring forces that are free of quantum anomalies! The Type C heptagon is a representation of the 295 SLs up to Chesed of the 49th Tree, just as the Type A 49-gon is, because both polygons have 295 yods. As the Type C heptagon is the fourth in the sequence of successive types of heptagons:
heptagon → Type A heptagon → Type B heptagon → Type C heptagon →
this illustrates the Tetrad Principle formulated in Article 1, according to which the fourth member of a class of mathematical object is (or embodies) a characteristic parameter of holistic systems (in this case, the number 295). It is exemplified par excellence by the Type C hexagon (the fourth class of the fourth type of regular polygon), which contains 248 yods outside its root edge that surround its centre:
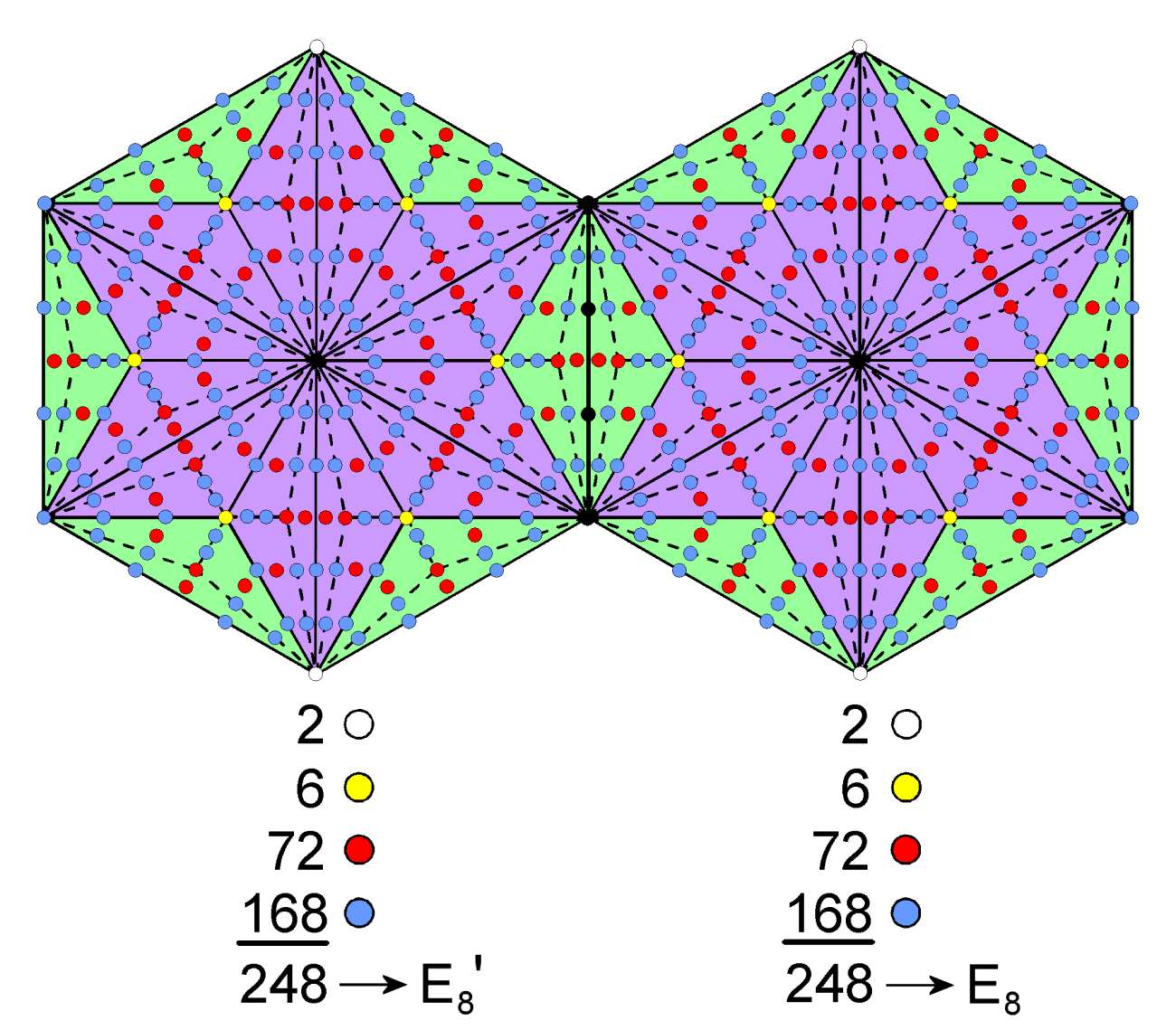
The two white yods denote the two simple roots of E8 that are not simple roots (denoted by the six yellow yods) of its exceptional subgroup E6, which has 72 roots denoted by the 72 red yods, the remaining 168 roots being denoted by the 168 blue yods. Also illustrated here is the amazing power of the tetractys to reveal in sacred geometries numbers of prime significance to theoretical physics (in this case, the dimension 496 of E8×E8′, one of the two possible symmetry groups describing the anomaly-free forces between heterotic superstrings). See also here.
| << Previous 1 [2] Next >> |