| << Previous 1... 11 12 [13] 14 15 Next >> |

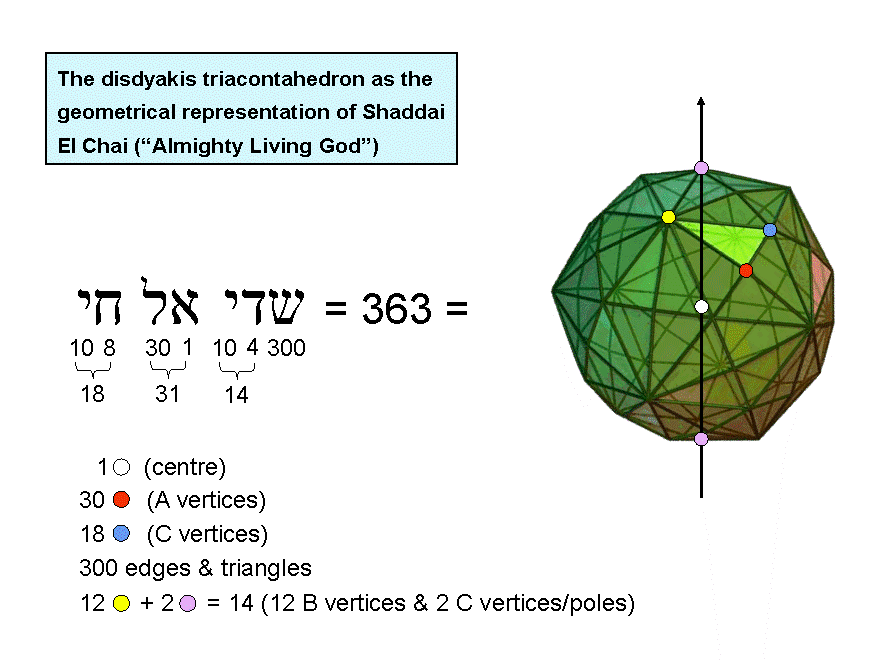
The disdyakis triacontahedron has 62 vertices that consist of 30 A vertices (red dot), 12 B vertices (blue dot) and 20 C vertices (yellow dot). The B vertices are vertices of an icosahedron and the C vertices are the vertices of a dodecahedron. Surrounding an axis that passes through two diametrically opposite C vertices (pink dots) and the centre of the polyhedron (white dot) are 180 edges & 120 triangular faces, i.e., 300 edges & triangles. The polyhedron consists of (62+300=362) vertices, edges & triangles. Including its centre, there are 363 geometrical elements. This is the number value of SHADDAI EL CHAI ("Almighty Living God"), the complete Godname of Yesod, which is the penultimate Sephirah of the Tree of Life. EL CHAI with number value 49 prescribes the centre (E = 1), the 30 A vertices (L = 30) and 18 C vertices (CHAI = 18) surrounding the axis. The value 300 of the letter shin (ש) in SHADDAI is the number of edges & triangles. The sum (14) of the letters daleth (ד) and yod (י) in SHADDAI is the sum of the number of B vertices (yellow dots) and the number of C vertices (pink dots) at the north & south poles of the polyhedron.
Such detailed correspondence between the values of the letters making up an ancient Hebrew Name of God and numbers of geometrical elements refutes as highly improbable the suggestion that it could be coincidence that the geometry of the disdyakis triacontahedron embodies the number of SHADDAI EL CHAI. Instead, it is a clear illustration of how the Godnames of the ten Sephiroth prescribe the mathematical properties of this extraordinary object — the polyhedral representation of the outer form of the Tree of Life. Indeed, the simplest example of this is the fact that each half of this polyhedron comprises 31 vertices (one vertex acting as its pole & 30 other vertices). This is the number value of EL (אל), the Godname of Chesed, meaning "God." The letter alef (E = 1) denotes a pole and the letter lamed (L = 30) denotes the 30 other vertices in each half.
| << Previous 1... 11 12 [13] 14 15 Next >> |