Home

12. Arithmetic connections between the 4₂₁ polytope and the Tree of Life

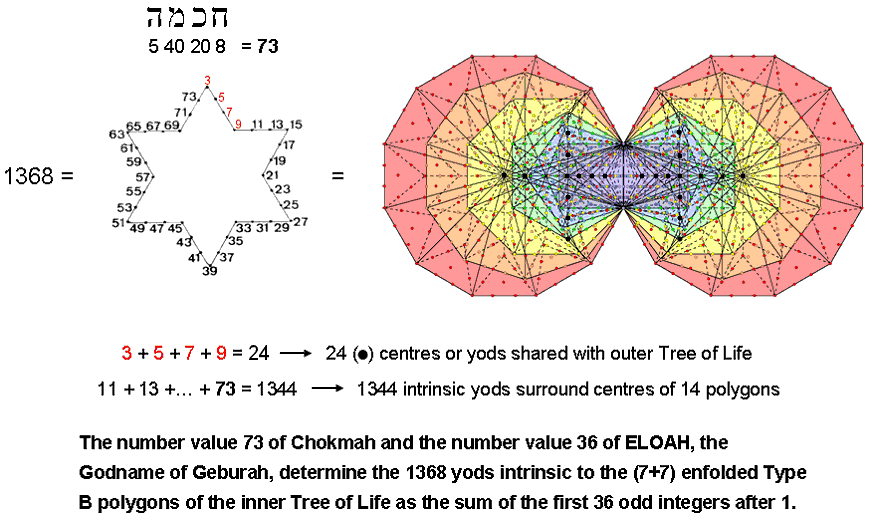
As 672 = 4×168 = 8×84 and 24 = 8×3, the number of vertices in the 4₂₁ polytope = 240 = 80×3 and its number of edges = 6720 = 80×84, so that its number of vertices & edges = 80×(3+84) = 6960 = 80×87. Remarkably, 80 is the number of Yesod and 87 is the number value of Levanah, its Mundane Chakra! Suppose that its 60480 triangular faces are tetractyses (ordinary, Type A, Type B, etc). The number of hexagonal yods lining their edges = 2×6720 = 13440 = 80×168, where 168 is the number value of Cholem Yesodoth, the Mundane Chakra of Malkuth. Given that Malkuth follows Yesod in the Tree of Life, this is equally remarkable. The number of yods lining the edges of the 4₂₁ polytope constructed from tetractyses = 240 + 2×6720 = 13680 = 80×3 + 80×168 = 80×171 = 10×36×38 = 10(37² − 1) = 10×(3 + 5 + 7 +... + 73), i.e., the Godname ELOHA of Geburah with number value 36 quantifies the shape of the polytope because 13680 is ten times the sum of the first 36 odd integers after 1 up to 73, which is the number of Chokmah:

As 36 yods line the boundary of a Star of David, assigning these 36 odd integers to them generates the number 1368, which was pointed out on #2 to be the number of yods intrinsic to the (7+7) enfolded Type B polygons (see diagram above). As 24 = 3 + 5 + 7 + 9, the first four odd integers (written above in red) sum to the number (24) of black centres or yods intrinsic to these polygons that are shared with the outer Tree of Life; they form one side of the Star of David. The next 32 odd integers add up to 1344, which is the number of yods unshared with the outer Tree of Life that surround centres of the 14 polygons. The 240 centres or yods shared with 10 Trees of Life denote the 240 vertices of the 4₂₁ polytope and the 13440 yods surrounding the centres of the 140 polygons enfolded in 10 Trees correspond to the 13440 hexagonal yods on the 6720 edges of the polytope:

The number of faces of the 4₂₁ polytope = 60480 = 9×6720. The number of edges & faces = 6720 + 9×6720 = 10×6720 = 67200 = 50×1344. In other words, it is the number of yods intrinsic to the 700 polygons enfolded in 50 Trees that surround their centres. It shows how ELOHIM, the Godname of Binah with number value 50, prescribes the number of edges & faces in the 4₂₁ polytope. Joining its 480 vertices to its centre generates 6720 internal triangles with 240 internal sides. The number of geometrical elements surrounding the centre of the polytope = 240 + 67200 + 240 + 6720 = 74400 = 31×2400 = 620×120, where 620 is the number value of Kether. This is a beautiful property because the number of hexagonal yods in a ten-sided decagon with 2nd-order tetractyses as sectors is 620, whilst 120 = 11² − 1 = 3 + 5 + 7 +... + 21, i.e., it is the sum of the first ten odd integers after 1. Assigning 120 to each hexagonal yod in this decagon generates the minimum number of geometrical elements needed to construct the interior and faces of the 4₂₁ polytope:

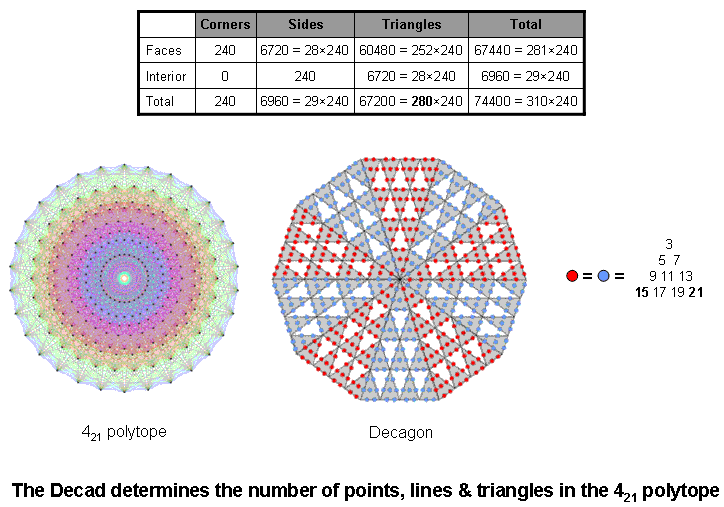
The Pythagorean Decad arithmetically determines the geometrical composition of the very polytope that represents the 240 roots of the exceptional Lie group E₈ used in E₈×E₈ heterotic superstring theory. Notice in the table that the numbers of sides and triangles are integer multiples of the number of vertices (240). In particular, the number of triangles = 280×240, where 280 is the number of Sandalphon, the Archangel of Malkuth. This is also the number of edges & faces. The total number of corners, sides & triangles = 31×10×240, where 31 is the number of EL, the Godname of Chesed, so that the number of such geometrical elements in each half of the polytope = 155×240, where 155 is the number value of ADONAI MELEKH, the complete Godname of Malkuth. We see that the gematria numbers of both the Godname and Archangel of Malkuth, the physical manifestation of the Tree of Life blueprint, are present in the geometrical composition of the 4₂₁ polytope. This, of course, is not unexpected, given its fundamental, mathematical status in representing the roots of the Lie symmetry group E₈ describing the forces between one of the two types of heterotic superstrings — the microphysical realisation of this blueprint.

The table shown below gives the numbers of yods in the 4₂₁ polytope when its faces and interior triangles are tetractyses:

(13440+60480=73920=308×240) hexagonal yods are in its faces, leaving (240+7200=7440=31×240) yods either as vertices or inside it. 154×240 hexagonal yods are in the 30240 faces in each half of the polytope, where 154 is the 153rd integer after 1. This shows how ELOHIM SABAOTH, the Godname of Hod with number value 153, prescribes the form of the 4₂₁ polytope. (240+480=720=6!) yods line the 240 internal sides, leaving (13440+60480+6720=80640=16×7!) yods, that is, (40320=8!) yods in each half. The number of hexagonal yods lining the 6960 sides = 13920 = 58×240 = 87×2×80, so that (87×80=6960) hexagonal yods line the 3480 sides in each half. As we saw earlier, this is the number of vertices & edges in the polytope. It is determined by the numbers of Yesod and Levanah, the Mundane Chakra of this Sephirah.

According to the table, the number of yods lining the edges of the 4₂₁ polytope = 240 + 56×240 = 57×240 = 19×3×240 = 19×720 = 19×6!. Assigning the tenth odd integer (19) to each of the 720 yods surrounding the centre of a decagon with 2nd-order tetractyses as sectors generates the number of yods needed to shape the 4₂₁ polytope. This is another way in which the Decad determines the properties of this holistic sacred geometry. The number of hexagonal yods at the centres of its faces = 252×240 = 84×720 = 84×6! = 12×7!. The total number of yods in its faces = (19+84=103)×6!. 103 is the gematria number value of Sabaoth ("Hosts"), part of the Godnames of Netzach and Hod. The number of internal yods = 30×240 = 10×6!. The total number of yods = (19+84+10=113)×6! = (1+112)×6! = 6! + 112×6!, where 6! is the number of yods on the sides of internal triangles and 112×6! (=16×7!) is the number of remaining yods. 112 is the number value of Beni Elohim, the Order of Angels assigned to Hod. The number 113 is the 30th prime number, where 30 = 1² + 2² + 3² + 4². Alternatively, 112×6! = 7×16×3×240 = 48×1680.

Constructed from tetractyses, the 421 polytope has 240 vertices and 2×6720 hexagonal yods on its edges.	There are 240 white yods that are either distinct centres of the 140 separate polygons in the inner form of 10 Trees of Life or yods shared between the latter and the 20 hexagons. (14×48=672) yods other than corners surround the centres of each set of the 7 polygons. The 140 polygons have (2×672×10=2×6720) such yods.

When the faces of the 4₂₁ polytope are tetractyses, there are (3360×2=6720) hexagonal yods on the 3360 edges in each half of it. We saw earlier that this is the number of yods surrounding the centres of the set of seven enfolded Type B polygons enfolded in each one of 10 Trees of Life that are unshared with them. It will now be shown that the same property applies to these polygons when separate. A Type B n-gon contains (15n+1) yods, where "1" denotes the yod at its centre. Given an n-gon divided into its sectors,14n more yods are needed to turn its sectors into Type A triangles. The seven separate Type B polygons have 48 sectors. Their transformation into Type A triangles requires (14×48=672) more yods. 6720 more yods are needed to turn into Type B polygons the 70 polygons in each half of the inner form of 10 Trees of Life when they are regarded as separate. The centre of the enfolded triangle and the seven yods on the vertical axis of the enfolded hexagon coincide with yods in triangles belonging to the outer Tree of Life. The number of centres of each set of seven separate polygons and shared yods = 1 + 7 + 5 = 13. One of them (Chokmah) is Netzach of the next higher Tree. Therefore, the number of shared yods or centres in n Trees and their 14n separate polygons = 12n + 1 + 12n + 1 = 24n + 2. This means that there are 240 shared yods or centres that are intrinsic to 10 overlapping Trees because they are not shared with the 11th Tree. They are the counterpart of the 240 vertices of the 4₂₁ polytope. The shared outer form of 10 Trees of Life and their inner form as separate polygons represent the 13680 yods that are needed to create the edges of the 4₂₁ polytope. As we saw earlier, the inner form of 10 Trees by itself embodies this number as the yod population of their enfolded polygons. The crucial number to be accounted for here is the number 6720, namely, the number of edges of the 4₂₁ polytope. It emerges naturally as:

• the number of yods that are intrinsic to the inner form of 10 Trees of Life and which surround centres of enfolded polygons;
• the number of yods needed to turn into Type A triangles all the (48×10=480) sectors of the 70 separate polygons present in the inner form of 10 Trees of Life: 10×48×14 = 6720.

In the second case, a pair of hexagonal yods on each edge of the polytope corresponds to a yod in one set of 70 polygons and its counterpart in the mirror image set of 70 polygons on the other side of the central pillar of the 10 Trees. Just as the 6720 edges give shape to the polytope whose vertices are 240 points distributed in 8-dimensional space, so the inner form of 10 Trees of Life is given form by 6720 yods other than the 240 centres of polygons and the yods they share with the outer form of these Trees. It cannot be a coincidence that the number of edges is equal to the number of plane-polarised waves that make up the 3360 circularly polarised oscillations in one revolution of the 10 whorls of the UPA recorded by Annie Besant & C.W. Leadbeater over a century ago.

The following additional comments need to be added:

• The table above indicate that the number of hexagonal yods in the faces of the 4₂₁ polytope = 308×240 = 44×1680 = 11×4×5×336 = 55×2×672. The number 55 is the tenth triangular number: 

55 = 1 + 2 + 3 + 4 + 5 + 6 + 7 + 8 + 9 + 10,

and 2×672 = 1344, which is the number of yods intrinsic to the (7+7) enfolded Type B polygons that surround their centres. As 1680 = 6×280, the number of hexagonal yods = 44×6×280 = 264×280 = 73920. In other words, assigning the number 280 of Sandalphon, the Archangel of Malkuth, to the 264 yods in the seven enfolded Type A polygons generates the number of hexagonal yods in the faces of the 4₂₁ polytope:

As 55 = 1² + 2² + 3² + 4² + 5² and 2×672 = 4×168 = 4×4×84 = 2²×2²×(1²+3²+5²+7²), the number of hexagonal yods in faces = (2²+4²+6²+8²+10²)×(2²+6²+10²+14 ²).

• The number of hexagonal yods on the edges of the polytope = 56×240 = 48×280 = 8×1680 = 80×168. In other words, assigning the number 168 of Cholem Yesodoth, the Mundane Chakra of Malkuth, to each of the 80 yods in the 1-tree that represents the most Malkuth level of the Cosmic Tree of Life generates the number of hexagonal yods that shape the faces of the 4₂₁ polytope. This is remarkable evidence of its Tree of Life nature. 
• The number of hexagonal yods at the centres of the faces = 252×240 = 216×280 = 36×1680 = 360×168. Comparing the three hexagonal yod populations 264×280, 48×280 & 216×280, the division 264 = 48 + 216 manifests in the seven enfolded polygons of the inner Tree of Life as the 216 yods lining the sides of their 47 tetractyses that are intrinsic to them in the sense that they are unshared with polygons enfolded in the next higher Tree and as the 48 yods that are either shared or centres of tetractyses. 
• The number of hexagonal yods at the centres of internal triangles = 28×240 = 24×280 = 4×1680 = 40×168. 
• The total number of hexagonal yods at centres of all tetractyses = 240×280 = 40×1680 = 400×168. 
• The total number of hexagonal yods = (2+56+252+28)×240 = (2+336)×240 = 2×240 + 288×280 = 2×240 + 48×1680 = 2×240 + 480×168 = 480×169. 
• The total number of yods = 240 + 480×169 = 240 + 240×338 = 339×240. The number 339 has a geometrical meaning in terms of the inner Tree of Life because the number of points, lines & triangles making up the (7+7) enfolded Type A polygons is 349, but 10 of these are the five points & lines making up the two side pillars of the outer Tree of Life that coincide with the vertical axes of the two hexagons, so that 339 geometrical elements are intrinsic to its inner form. The 349 geometrical elements comprise the three geometrical elements making up the root edge (two points & one line) and 168 elements making up each set of seven enfolded polygons. This corresponds to, respectively, the three sets of 240 yods (240 vertices & 240×2 hexagonal yods on sides of internal tetractyses) and 168 multiples of 240 hexagonal yods in the edges, faces & internal tetractyses of each half of the polytope. The (168+3+168)×10 division of geometrical elements in the inner form of 10 Trees becomes for the 4₂₁ polytope the (168+3+168)×10×24 division of yods. They are the same pattern apart from a factor of (24=4!). 
• The number of hexagonal yods on the sides of all tetractyses = 240 + 58×240 = 59×240. The number of yods not lining sides = (339−59=280)×240. The number of yods not lining edges = (339−57=282)×240, where 282 is the number value of Aralim, the Order of Angels assigned to Binah. 
• The number of hexagonal yods in the edges and the centres of the faces and internal triangles = (56+252+28=336)×240. It is remarkable that this number is the product of the superstring structural parameter 336 (number of turns in one revolution of a whorl of the UPA), which is embodied in many sacred geometries, and the 240 roots of the exceptional Lie group E₈, which describes the symmetry of the unified force between one of the two types of heterotic superstrings. 
• The (336×240=48×1680) hexagonal yods that either line edges or are at centres of tetractyses comprise 36×1680 hexagonal yods in faces, 8×1680 hexagonal yods on edges and 4×1680 hexagonal yods at centres of internal tetractyses. The 48 corners of the seven separate polygons in the inner Tree of Life become the 36 corners of the enfolded ones, (4+8=12) corners disappearing in the enfoldment. Its counterpart in the 48 corners are the 12 corners of the triangle, square & pentagon and the 36 corners of the last four polygons. It is remarkable that assigning the superstring structural parameter 1680 paranormally derived by the Theosophists Besant & Leadbeater to the 48 corners of the seven separate polygons should reproduce the various populations of hexagonal yods needed to construct the 4₂₁ polytope from tetractyses. It demonstrates the Tree of Life character of this polytope.

Using the results obtained in #36 of Wonders of superstrings:

16800 = 10⁴(1²+2²+3²+...+31²)⁄(2²+3²+4²+...+26²)

and

168×248 = 2² + 4² + 6² + ... + 62²,

where 31 is the number value of EL (the Godname of Chesed), 62 is the number value of Tzadkiel (its Archangel), 26 is the number of YAHWEH (the Godname of Chokmah) and 248 is the number of Raziel (its Archangel), the number of edges in the 4₂₁ polytope = 6720 = 4×1680 = 2²×16800/10 = 10³(2²+4²+6²+..+62²)/(2²+3²+4 ²+...+26²), so that

6720 = 16800×2480/(2²+3²+4²+...+26²).

This amazing equation expresses the 6720 edges of the 4₂₁ polytope in terms of the 16800 circularly polarised waves in the ten whorls of the UPA/E₈×E₈ heterotic superstring, the number (2480) of superstring space-time components of the 248 10-dimensional gauge fields of the symmetry group E₈ whose roots are represented by this polytope and the 26 dimensions of the space-time of bosonic strings in which the superstring is embedded. Let no one contend that this connection between a number (16800) paranormally obtained by Annie Besant & C.W. Leadbeater over a century ago and three numbers (6720, 2480, 26) rigorously derived from pure mathematics and (super)string theory could be due to chance!

The equation highlighted above gives:

16800 = 672(2²+3²+...+26²)/248 = 1344(2²+3²+...+26²)/496.

As 336 = (1²+2²+...+31²)/31,

1344 = 4×336 = 2²×336 = (2²+4²+...+62²)/31

and

16800 = (2²+3²+...+26²)(2²+4²+...+62 ²)/31×31×16 = (2²+3²+...+26²)(1²+2²+...+31 ²)/31²×4.

Therefore,

67200 = 4×16800 = (2²+3²+...+26²)(1²+2²+...+31 ²)/31².

The 4₂₁ polytope has 6720 edges and 60480 triangular faces, i.e., 67200 edges & faces. We discover that the number values 26 and 31 of, respectively, YAHWEH (Godname of Chokmah) and EL (Godname of Chesed) arithmetically determine the number of geometrical elements that shape the faces of the 4₂₁ polytope. This is further evidence for the archetypal nature of this polytope.

<< Previous    1...   10  11  [12]  13  14  ...24    Next >>

Home