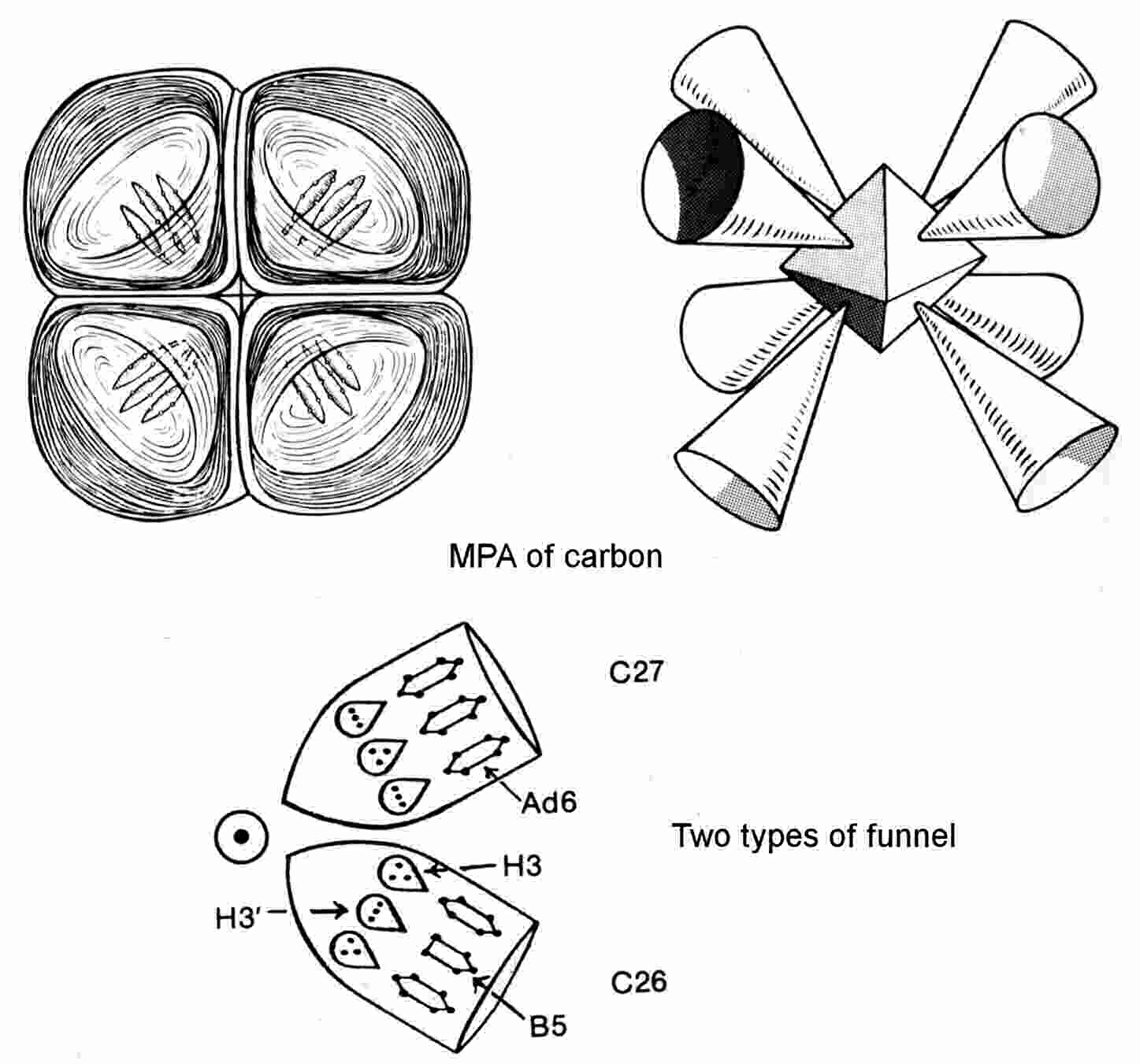
The Carbon MPA
The carbon MPA is an octahedral array of eight funnels that project from a central sphere containing four free UPAs. The funnels are of two types: four C27 funnels, each containing three Ad6 groups, two linear H3′ triplets and one H3 triplet, and four C26 funnels, each containing two Ad6 groups, one B5 group, two H3 triplets and one H3′ triplet. In the C27 funnel, the H3 triplet lies between the two H3′ triplets; in the C26 funnel, the H3′ triplet lies between the two H3 triplets.
Carbon MPA = 4 + 4C27 + 4C26.
|
|
 |
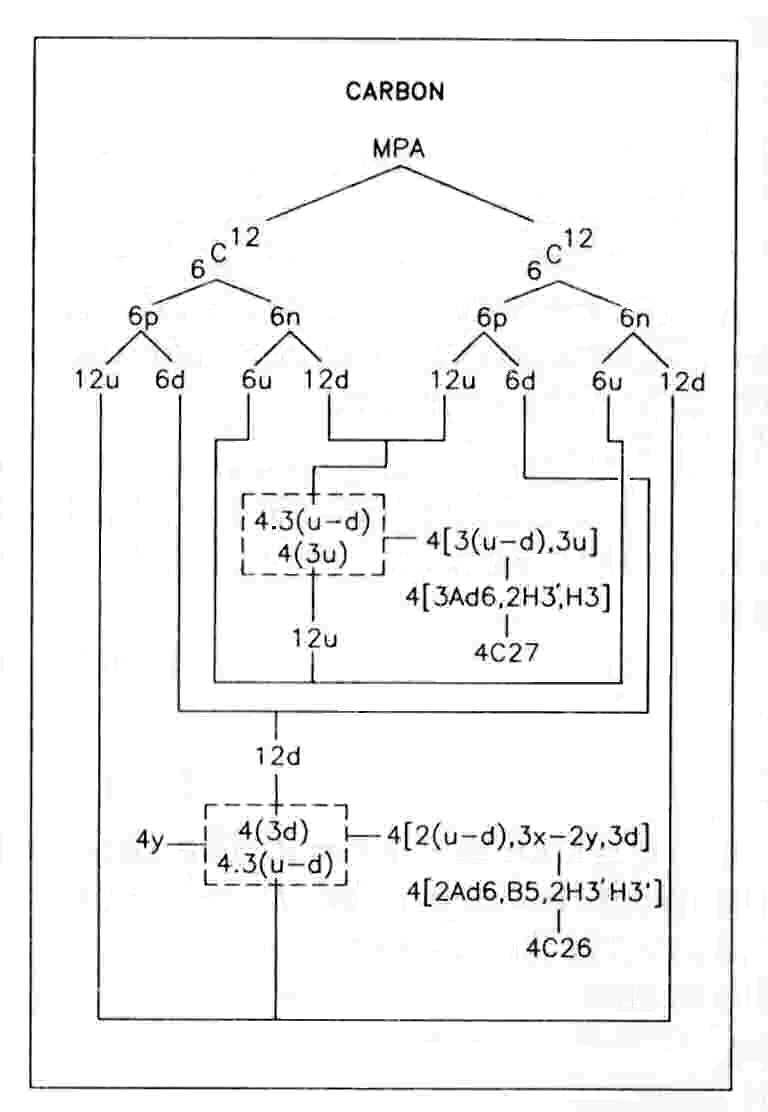
The carbon MPA is formed from two C12 nuclei, which provide 216 subquarks — the same as the number of UPAs. These make up thirty-six u quarks and thirty-six d quarks, of which twenty-four u quarks and twelve d quarks form the particles in the C26 funnels and the four UPAs that link a pair of C26 and C27 funnels. But for these linking UPAs, a C27 would be the mirror state of a C26. In fact — apart from the B5 group in the C26, which has no counterpart in the C27 — each particle in one funnel is the mirror state of its counterpart in the other type.
In each C27 funnel, there are three u-d diquarks (Ad6) and three u quarks (2H3′+H3). These have
a total electric charge of +3. The four C27 funnels therefore have a charge of +12. As the MPA is formed from two
carbon nuclei with twelve protons, it has a charge of +12, i.e., the total electric charge of all the particles in
the four C27 funnels is the same as that of the two parent carbon nuclei. Each of the remaining identical funnels
would therefore contain twenty-seven UPAs with a total electric charge of zero if the MPA had no
 central core. As explained in detail in the author's book Extra-sensory Perception of Quarks, the total electric charge of the particles
inside a funnel cannot be zero because, when an MPA is formed from the nuclei of two atoms, the charged
subquarks released from each nucleus interact with the local electromagnetic field environment generated by the
valence electrons of the two atoms. It is this Coulombic interaction that shapes MPAs having funnels, explaining
why the number of funnels in an MPA is twice the valence of its corresponding element and why the shapes of MPAs
correlate with the positions of their elements in the Periodic Table. Hence, one or more UPAs of negative charge
must be absent from a funnel that would otherwise have zero net charge in order to leave the other particles in
the funnel with a net positive charge. According to Occult Chemistry: "In the centre of the octahedron
is a globe containing four Anu, each within its own wall; these lie on the dividing lines of the faces and
each holds a pair of funnels together (author's italics). It seems as though this Anu had been
economically taken from one Ad6 in the funnels to form the link."1 Since it is
""within its own wall," it must be a free subquark, that is, one which is not bound by strings to any subquarks
in the funnels. The particles in each pair of funnels linked by a free UPA must therefore be bound by purely
electromagnetic forces to their single UPA nucleus, so that, as the particles in a C27 funnel have a net
positive charge, this UPA must be negatively charged in order to hold together both positively charged types of
funnel. In other words, the UPA must be a Y subquark, which has an electric charge of −4/9. This prediction is
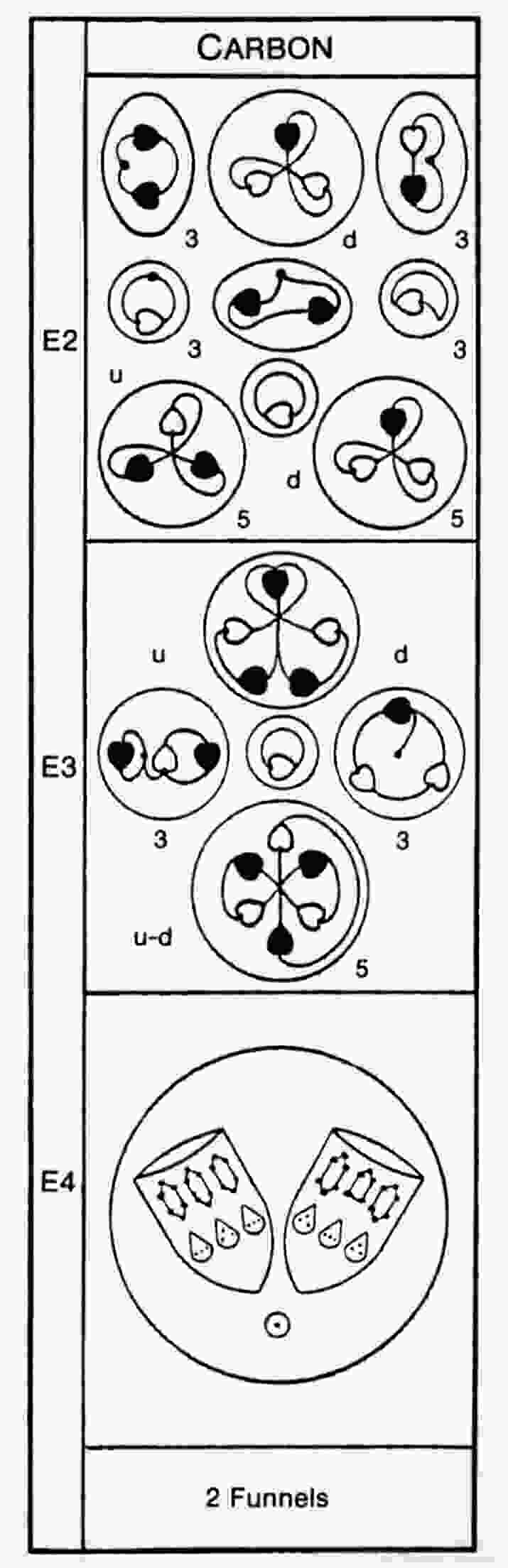
confirmed by the disintegration diagram for a pair of linked funnels for the following reason: the diagram shows
that the B5 group breaks up at stage E2 into a (−) triplet (d quark) and a (+) duad (X-X). As all the Ad6 groups
should be u-d diquarks (this is confirmed by the fact that the five Ad6 groups break up at stage E2 into five
(+) triplets (u quarks) and five (−) triplets (d quarks)), the UPA "economically taken from one Ad6" must be a
negatively charged Y subquark because:
central core. As explained in detail in the author's book Extra-sensory Perception of Quarks, the total electric charge of the particles
inside a funnel cannot be zero because, when an MPA is formed from the nuclei of two atoms, the charged
subquarks released from each nucleus interact with the local electromagnetic field environment generated by the
valence electrons of the two atoms. It is this Coulombic interaction that shapes MPAs having funnels, explaining
why the number of funnels in an MPA is twice the valence of its corresponding element and why the shapes of MPAs
correlate with the positions of their elements in the Periodic Table. Hence, one or more UPAs of negative charge
must be absent from a funnel that would otherwise have zero net charge in order to leave the other particles in
the funnel with a net positive charge. According to Occult Chemistry: "In the centre of the octahedron
is a globe containing four Anu, each within its own wall; these lie on the dividing lines of the faces and
each holds a pair of funnels together (author's italics). It seems as though this Anu had been
economically taken from one Ad6 in the funnels to form the link."1 Since it is
""within its own wall," it must be a free subquark, that is, one which is not bound by strings to any subquarks
in the funnels. The particles in each pair of funnels linked by a free UPA must therefore be bound by purely
electromagnetic forces to their single UPA nucleus, so that, as the particles in a C27 funnel have a net
positive charge, this UPA must be negatively charged in order to hold together both positively charged types of
funnel. In other words, the UPA must be a Y subquark, which has an electric charge of −4/9. This prediction is
confirmed by the disintegration diagram for a pair of linked funnels for the following reason: the diagram shows
that the B5 group breaks up at stage E2 into a (−) triplet (d quark) and a (+) duad (X-X). As all the Ad6 groups
should be u-d diquarks (this is confirmed by the fact that the five Ad6 groups break up at stage E2 into five
(+) triplets (u quarks) and five (−) triplets (d quarks)), the UPA "economically taken from one Ad6" must be a
negatively charged Y subquark because:
u-d [= (2X-Y)-(X-2Y)] → 3X-2Y + Y
and
3X-2Y → X-2Y (= d) + X-X.
Notice that, according to the disintegration diagram, the three H3 triplets in a pair of funnels break up at stage E2 into three (0) duads and three UPAs. This is consistent with the basic identification of a (0) duad as an X-Y bound state and with these triplets being d quarks, i.e., X-2Y bound states:
d (=X-2Y) → X-Y + Y.
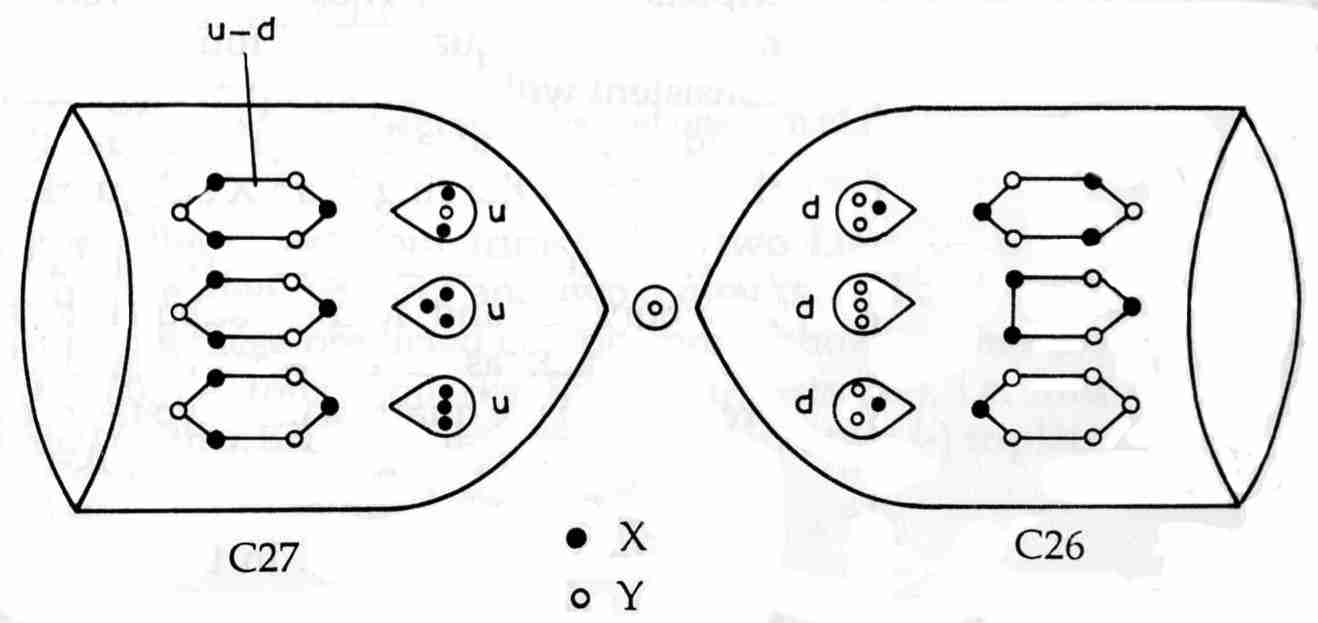
The predicted subquark composition of the particles contained in a pair of C26 & C27 funnels is shown below:
References