| << Previous 1... 8 9 [10] 11 12 ...56 Next >> |
#10 How the number of Binah determines the form of the E8×E8 heterotic superstring

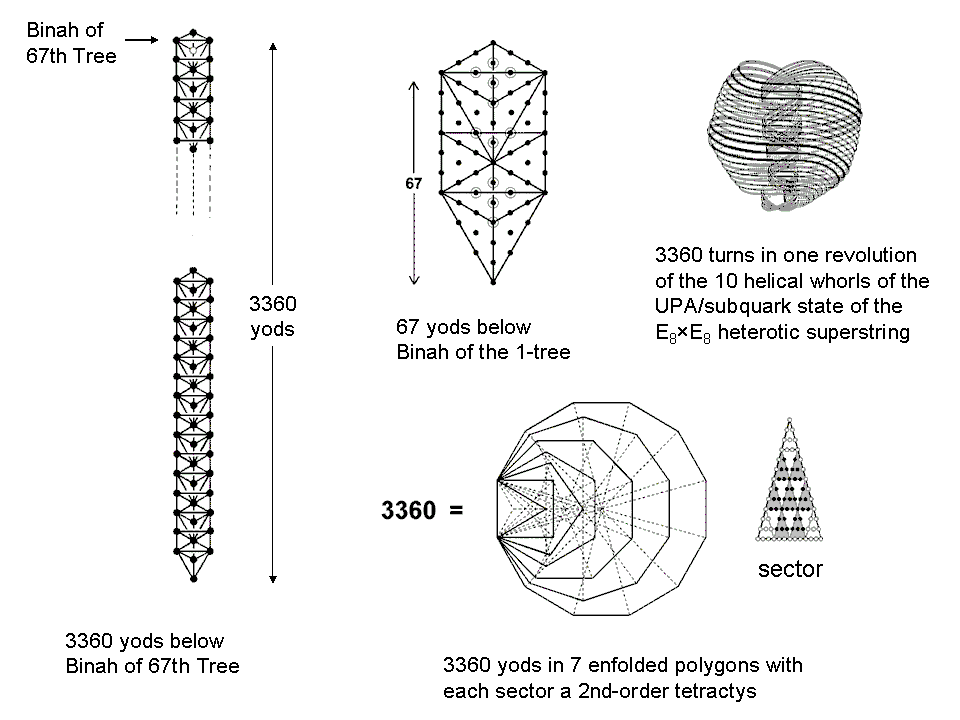
Using the formula introduced in #9, the number of yods in 67 overlapping Trees of Life = Y(67) = 3370. The topmost tetractys has 10 yods. Therefore, the number of yods below Binah of the 67th Tree of Life = 3370 – 10 = 3360. Now, 67 is the number value of Binah. It is also the number of yods below Binah of the lowest Tree of Life, thus showing the geometrical basis of the Hebrew name of the third Sephirah.
As pointed out earlier, one revolution of the 10 helical whorls of the UPA/superstring contains 3360 circular turns. The Tree of Life character of this superstring structural parameter is demonstrated par excellence by the fact that the seven enfolded polygons of the inner Tree of Life have 3360 yods when their 47 sectors are 2nd-order tetractyses. The number value 67 of Binah therefore determines the number of circularly polarised oscillations made by the 10 whorls of the UPA as they revolve once around its axis of spin.
67 is the 19th prime number, where 19 is the 10th odd integer. The Pythagorean Decad determines the number 67 and therefore the oscillatory form of the superstring, as well as its 10-fold composite nature and its 10-dimensional nature.
| << Previous 1... 8 9 [10] 11 12 ...56 Next >> |