| << Previous 1... 13 14 [15] 16 17 ...81 Next >> |
#15 Correspondence between the 29 polyhedra contained in the disdyakis triacontahedron and the first (6+6) polygons enfolded in 10 Trees of Life

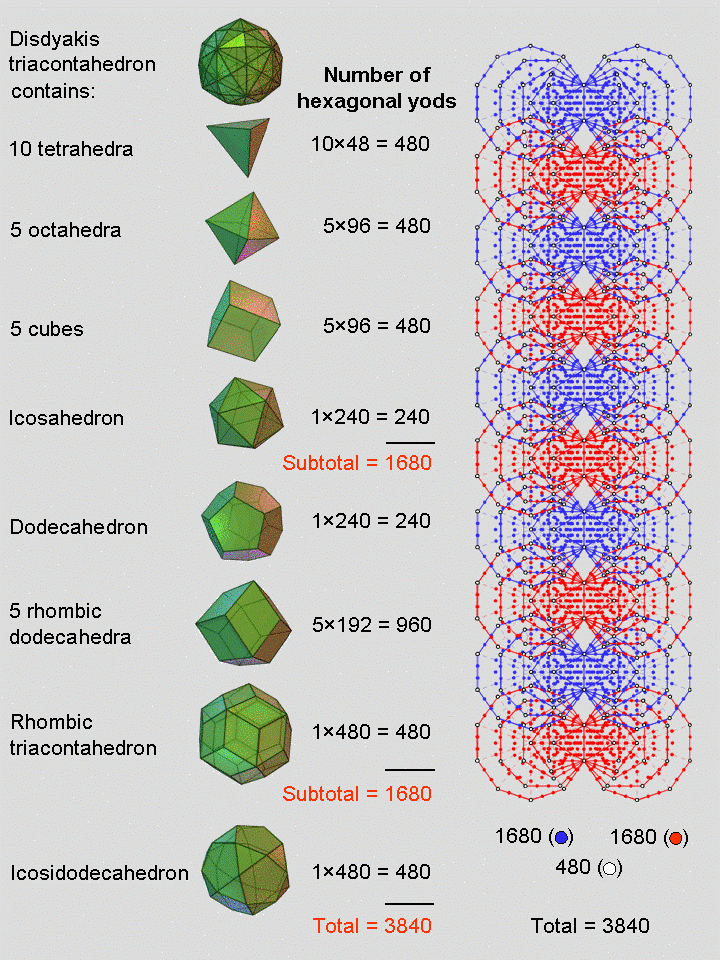
The 62 vertices of the disdyakis triacontahedron can accommodate ten tetrahedra, five octahedra, five cubes, an icosahedron, a dodecahedron, five rhombic dodecahedra, a rhombic triacontahedron and a icosidodecahedron (the dual of the lattermost) — see pages 6, 7 & 9 at Superstrings as sacred geometry/Disdyakis triacontahedron. When their faces are divided into their sectors and each sector turned into a tetractys, the 21 Platonic solids other than the dodecahedron contain 1680 hexagonal yods, the dodecahedron, the rhombic dodecahedra and the rhombic triacontahedron have 1680 hexagonal yods and the icosidodecahedron has 480 hexagonal yods. The faces of the 29 polyhedra have 3840 hexagonal yods.
Compare this pattern of numbers with the yods of the first (6+6) polygons enfolded in each of ten overlapping Trees of Life with their sectors turned into tetractyses. The 120 polygons have 482 white corners.* The highest corners of the two hexagons enfolded in the tenth Tree of Life coincide with the lowest corners of the hexagons enfolded in the next higher Tree of Life. This means that 480 corners are intrinsic to the 120 polygons (this is why the two shared, topmost corners of the hexagons enfolded in the tenth Tree of Life are not assigned white yods in the diagram opposite). There are 1680 yods other than corners in the 60 polygons on each side of the central Pillar of Equilibrium.** The 480 intrinsic corners correspond to the 480 hexagonal yods in the faces of the icosidodecahedron, the 1680 yods in the 60 polygons enfolded on one side of the Pillar of Equilibrium correspond to the 1680 hexagonal yods in the faces of the 21 Platonic solids of the first four types and the 1680 yods in the 60 polygons enfolded on the other side of the central pillar correspond to the 1680 hexagonal yods in the faces of the remaining seven polyhedra that can be fitted in the disdyakis triacontahedron. The reason why the corners of polygons correspond to the icosidodecahedron rather than to other sets of polyhedra with 480 hexagonal yods is that it is unique among the set of 29 polyhedra in being the only Archimedean solid, just as the corners of tetractyses are distinct from hexagonal yods because they symbolize the Supernal Triad instead of the Sephiroth of Construction.
This amazing correspondence is powerful evidence for the disdyakis triacontahedron being the polyhedral counterpart of the inner form of ten overlapping Trees of Life. The two geometries are the polygonal and polyhedral counterparts of the table of 64 hexagrams in the ancient Chinese system of divination called 'I Ching,' in which 168 lines & broken lines making up 28 hexagrams lie above and below the 48 lines & broken lines in its eight diagonal hexagrams (see here). The 48:336 division of diagonal and off-diagonal lines & broken lines is the counterpart of the 480 (=48×10) hexagonal yods in the icosidodecahedron and the 3360 (=336×10) hexagonal yods in the 28 other polyhedra. Whereas the 336 off-diagonal lines & broken lines in the 56 hexagrams signify the 336 circularly polarized waves in a complete revolution of a single whorl of the UPA/subquark superstring, the 3360 hexagonal yods in the faces of the 28 Platonic and Catalan solids generated by the disdyakis triacontahedron symbolize the 3360 circularly polarized waves in a complete revolution of the ten whorls of this basic unit of matter. The ten-fold nature of the Tao is only implicit in the table of hexagrams, which refer to the cycle of oscillations of a single whorl, not all ten whorls. Its explicit representation is the disdyakis triacontahedron, the polyhedral version of the inner form of ten Trees of Life that manifest in space-time as the ten whorls of the UPA/subquark superstring.
The superstring structural parameter 3360 is also embodied in the inner form of a single Tree of Life
as the number of yods in its seven enfolded polygons with 2nd-order tetractyses as their sectors (see here).
* Proof: the first six enfolded polygons have 26 corners. Both sets of these polygons have (26+24=50) corners. This shows how YAHWEH with number value 26 and ELOHIM with number value 50 prescribe these polygons as a holistic structure. The highest corners of the two hexagons coincide with the lowest corners of the two hexagons enfolded in the next higher, overlapping Tree of Life. Therefore, 48 corners are intrinsic to the two sets of the first six polygons enfolded in each overlapping Tree of Life. The number of corners of the 12n polygons of the first six types enfolded in n Trees of Life = 48n + 2. The 120 polygons of the first six types enfolded in ten overlapping Trees of Life have 482 corners.
** Proof: the number of yods in an N-gon whose N sectors are tetractyses = 6N + 1. The number of yods in an N-gon other than its corners = 5N + 1. The number of yods other than corners in the first six separate N-gons = Σ(5N+1) = 5ΣN + 6 = 5×36 + 6 = 186. The (6×4 = 24) yods on the six separate edges that coincide as the root edge when the polygons are enfolded become the four yods on this shared edge, i.e., 20 yods disappear (ten corners, ten hexagonal yods). A corner of the triangle becomes the centre of the hexagon, a corner of the pentagon becomes the centre of the decagon and five yods in a sector of the hexagon become yods in the triangle. The number of yods other than corners in the first six N-gons = 186 – 10 – 1 – 1 – 5 = 169. There are (169–2=167) such yods outside the root edge. Both sets of the first six enfolded polygons have (2×167 + 2 = 336) yods other than corners. (336/2 = 168) such yods are associated with each set. (10×168=1680) yods other than corners are associated with each set of the 60 polygons enfolded in ten overlapping Trees of Life. The number of yods other than corners in the 120 polygons of the first six types that are enfolded in ten Trees of Life = 2×1680 = 3360. The total number of yods in these polygons = 480 + 3360 = 3840.