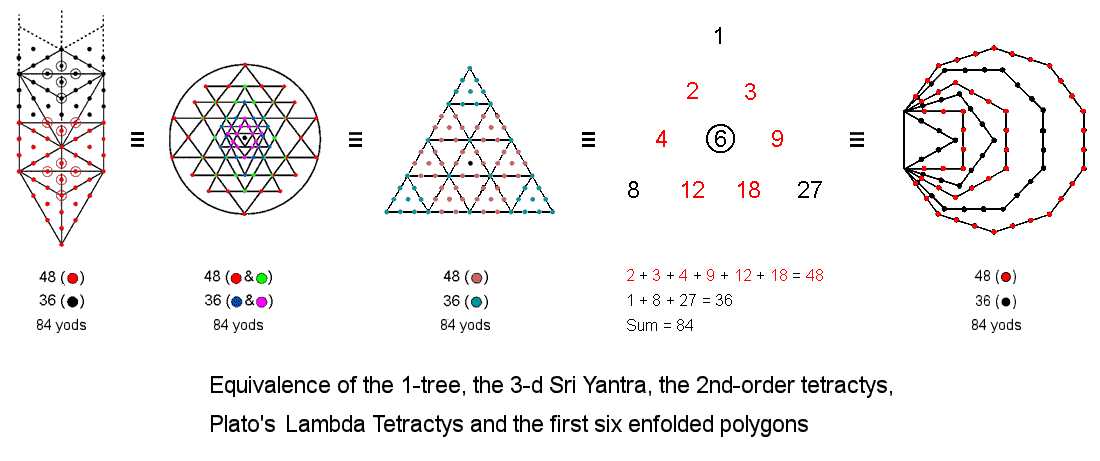
#2 Correspondence between the 1-tree, the 3-d Sri Yantra, the 2nd-order tetractys, the Lambda Tetractys & the first six enfolded polygons

Just as the Tree of Life is equivalent to the 2-dimensional Sri Yantra, so the 84 yods up to the top of the 1-tree are the counterpart of the 84 corners of the 42 triangles in four layers that surround the centre of the 3-dimensional Sri Yantra. The 48 red yods up to Chesed correspond to the 48 red & green corners of the triangles in the third & fourth layers; the 36 black yods above Chesed correspond to the 36 blue & violet corners of the triangles in the first two layers.

The 84 yods that surround the centre of the 2nd-order tetractys comprise 48 brown hexagonal yods that belong to the set of seven 1st-order tetractyses expressing the seven Sephiroth of Construction and 36 green yods either at corners of 1st-order tetractyses or in 1st-order tetractyses at the three corners of the 2nd-order tetractys.

The sum of the nine integers in the Lambda Tetractys that surround its central integer 6 is 84. It is the sum of 36 (the sum of the integers at its corners) and 48 (the sum of the six integers at the corners of a hexagon).

There are 84 yods outside the root edge that lie on the sides of the first six enfolded polygons. 36 black yods line the sides of the triangle, pentagon & octagon; 48 red yods line the sides of the square, hexagon & decagon.

The 36:48 division displayed by these representations of holistic systems expresses the metaphysical distinction between the subjective Supernal Triad and the objective Sephiroth of Construction. See also #29 in Sacred geometry/Correspondences.

The 1-tree has 69 hexagonal yods and 11 corners. Outside it are four hexagonal yods. The counterparts in the 2nd-order tetractys of these (69+15) yods are the 69 hexagonal yods surrounding its centre and the 15 corners of the ten 1st-order tetractyses. The counterpart of this 69:15 pattern in the Lambda Tetractys is the difference between the sum (69) of the integers 3, 9, 12, 18 & 27 and the sum (15) of the integers 1, 2, 4, & 8 on the left side of the tetractys.

Not only is the 1-tree analogous to the 2nd-order tetractys but so, too, is the Tree of Life, because the ten white corners of its 16 tetractyses and their 60 black, hexagonal yods are the counterparts of the ten white, hexagonal yods at the centres of the tetractyses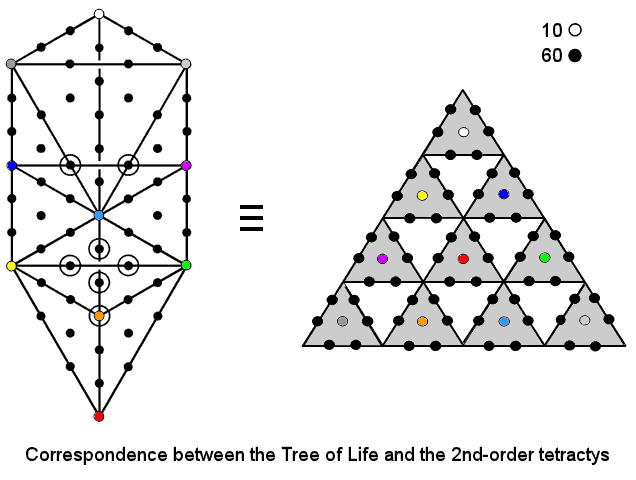

and their 60 black, hexagonal yods at the corners of hexagons. Although the correspondences for the Tree of Life and for the 1-tree are inconsistent with each other, this does not matter, as not all the yods in the former survive its transformation into the latter, so that this change is not simply a matter of 14 new yods being added. Some of the yods in the Tree of Life disappear when it becomes the 1-tree — a feature that cannot be represented merely by considering more aspects of a single representation. What is important is that the 2nd-order tetractys has the flexibility to be equivalent to both the Tree of Life and the 1-tree, although in different ways, as the latter is not simply the former with ten more yods added, e.g., the hexagonal yods at the centres of the Kether-Chokmah-Tiphareth & Kether-Binah-Tiphareth triangles disappear when the Tree of Life turns into the 1-tree because the straight line Path joining Kether and Tiphareth in the Tree of Life bends into the two lines joining Kether to Daath and Daath to Tiphareth in the 1-tree, so that two triangles/tetractyses disappear and five new triangles/tetractyses appear.

<< Previous    1  [2]  3  4  5  ...81    Next >>

Home