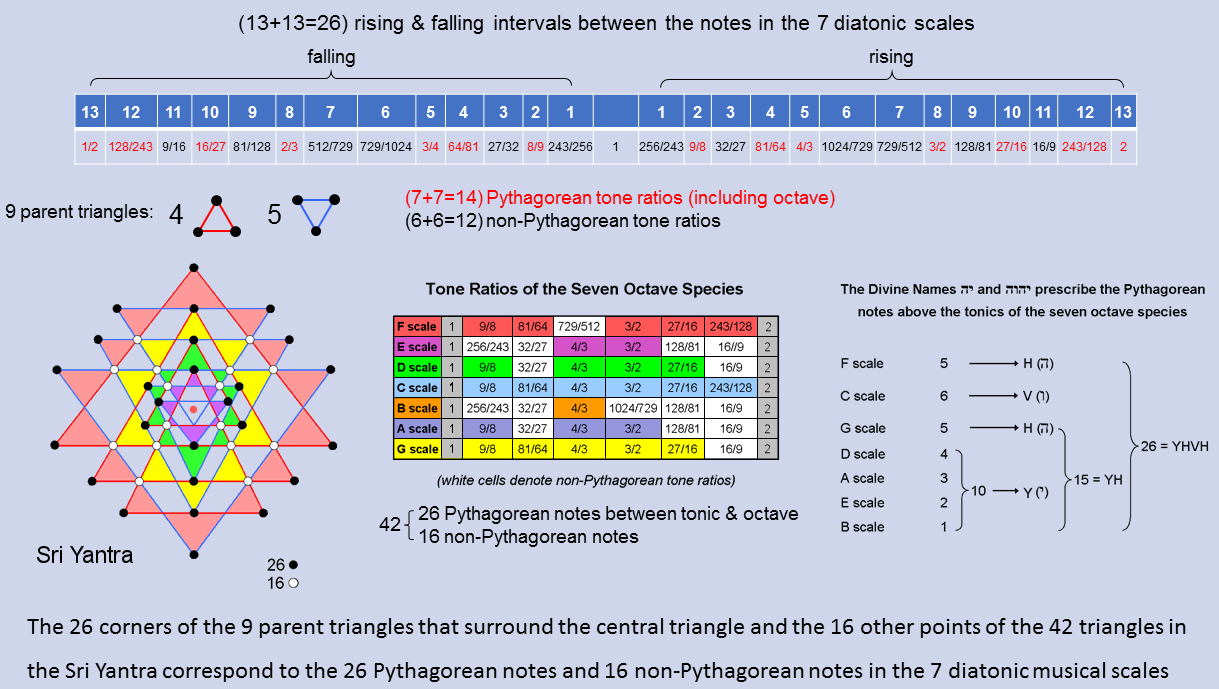
Including the octave, the 7 diatonic musical scales have 13 types of rising intervals.* They have 13 falling counterparts. Therefore, there are 26 types of rising & falling intervals between their notes. Formally counting the octave as a Pythagorean note because it belongs to the Pythagorean scale, there are (7+7=14) types of rising & falling, Pythagorean intervals (written in red in the diagram opposite) and (6+6=12) types of rising & falling, non-Pythagorean intervals (written in black).** This 14:12 division in the number 26 appears in the Sri Yantra as the 14 corners of the 5 downward-pointing (Shakti) triangles that surround the centre triangle and the 12 corners of the 4 upward-pointing (Shiva) triangles. The 42 triangles surrounding the central triangle have 26 points provided by the 9 parent triangles, leaving 16 other points. This 26:12 division appears in the 7 diatonic scales as the 26 Pythagorean notes and 16 non-Pythagorean notes that make up the (7×6=42) notes between their tonics and octaves. The Divine Name YAHWEH prescribes both features because the Sri Yantra and the 7 diatonic scales are analogous, holistic systems, the points of the 42 triangles in the former denoting their 42 notes. The gematria number values of the 4 letters of this Divine Name are the numbers of Pythagorean notes in various scales. Two alternative schemes to that shown are possible:

1. D & E scales → 6 (=V) and A, B, & C scales → 10 (=Y);
2. A, B & E scales → 6 (=V) and C & D scales → 10 (=Y).

The depicted scheme seems the most natural because it has more letters with number values that denote numbers of Pythagorean notes in a single scale.