
The 421 polytope has 6720
edges.
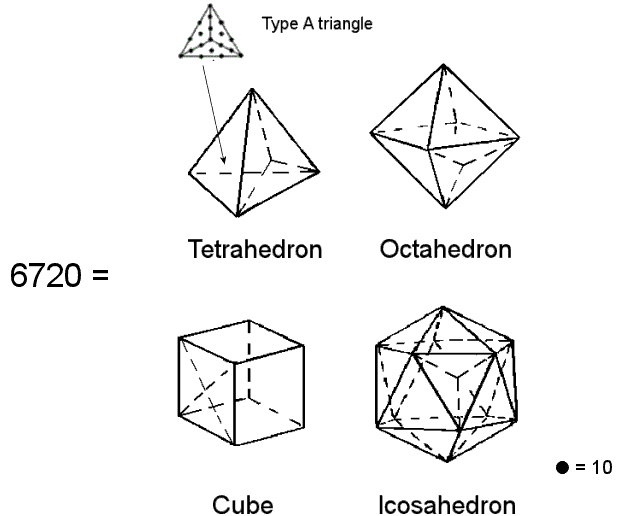
Constructed from Type A triangles, the first four Platonic solids embody the number 6720 when each yod is assigned the number 10.
| << Previous 1... 13 14 [15] 16 17 ...24 Next >> |
15. The first four Platonic solids embody the number of edges of the 421 polytope
 |
 |
|
|
Constructed from Type A triangles, the first four Platonic solids embody the number 6720 when each yod is assigned the number 10. |
Suppose that the 38 faces of the first four Platonic solids with 60 edges are constructed from Type A polygons. The 60 internal triangles formed by joining their vertices to their centres may be regarded as simple tetractyses or as Type A triangles. For the present purpose, only the former will be discussed here. The table shown below lists the yod populations of their faces and interiors:
Number of yods in the faces & interiors of the first four Platonic solids
| V | E | F |
Faces |
Interior |
Faces+Interior |
|||||||
| Number
of corners |
Number
of hexagonal yods |
Total | Number of corners |
Number of hexagonal yods |
Total | Number of corners |
Number of hexagonal yods |
Total | ||||
| Tetrahedron | 4 | 6 | 4 | 8 | 48 | 56 | 1 | 14 | 14+1 | 8+1 | 62 | 70+1=71 |
| Octahedron | 6 | 12 | 8 | 14 | 96 | 110 | 1 | 24 | 24+1 | 14+1 | 120 | 134+1=135 |
| Cube | 8 | 12 | 6 | 14 | 96 | 110 | 1 | 28 | 28+1 | 14+1 | 124 | 138+1=139 |
| Icosahedron | 12 | 30 | 20 | 32 | 240 | 272 | 1 | 54 | 54+1 | 32+1 | 294 | 326+1=327 |
| Total | 30 | 60 | 38 | 68 | 480 | 548 | 1 | 120 | 120+4 | 68+4 | 600 | 668+4=672 |
("1" denotes the centre of a Platonic solid).
Including their centres, the tetrahedron, octahedron, cube & icosahedron have 672 yods (124 internal, 548 in faces). On average, they have (672/4=168) yods made up of (124/4=31) internal yods and (548/4=137) yods in faces. Amazingly, the first four Platonic solids embody on average both the superstring structural parameter 168 discussed widely on this website and the number 137, one of the most important numbers in physics because its reciprocal measures the approximate value of the fine-structure constant! This number is the difference between 168, which is the number value of the Mundane Chakra of Malkuth, and 31, which is the number value of EL ("God"), the Godname of Chesed:
137 = 168 − 31.
137 is the average number of yods making up the faces of the first four Platonic solids when constructed from Type A triangles.
The Tetrad and the 2nd-order tetractys determine the yod population of the first four Platonic solids because 672 = 8×84, which means that an 8-fold array of 2nd-order tetractyses, each with 85 yods, contains 672 yods surrounding their shared apices:
| 672 = |  |
Now suppose that each of the 672 yods is weighted with the number 10. The first four Platonic solids then embody the number 6720. This is the number of edges in the 421 polytope. The average of the numbers generated by their weighted yods is 1680. This is the number of turns in each helical whorl of the UPA. It is the sum of the number 310 generated by their internal yods and the number 1370 generated by the yods in their faces. The latter number is the yod population of the inner Tree of Life with Type B polygons. In our discussion of the 24-cell, we found that its faces have 672 corners, lines & triangles in addition to its vertices & edges when constructed from Type A triangles. In our discussion in #12 of the arithmetic properties of the 421 polytope, we pointed out that, associated with each set of seven enfolded Type B polygons, there are 672 intrinsic yods surrounding their centres. These are the yods belonging solely to each set that actually create its form. The number 672 performs the same role in the context of the first four Platonic solids, only this time it quantifies the yods needed to create the analogous, holistic system in three, not two, dimensions of space. For the 24-cell, it determines its faces in four-dimensional space. Multiplied by the Decad, the number 672 quantified the edges that shape the faces of the 421 polytope in eight-dimensional space. In the case of the UPA/subquark superstring, it is the number of perpendicular plane waves differing in phase by 90° whose supposition creates 336 circular turns in each revolution of a whorl around the axis of spin of the UPA.
| << Previous 1... 13 14 [15] 16 17 ...24 Next >> |