The 1-tree has 84 yods
up to the level of its apex.
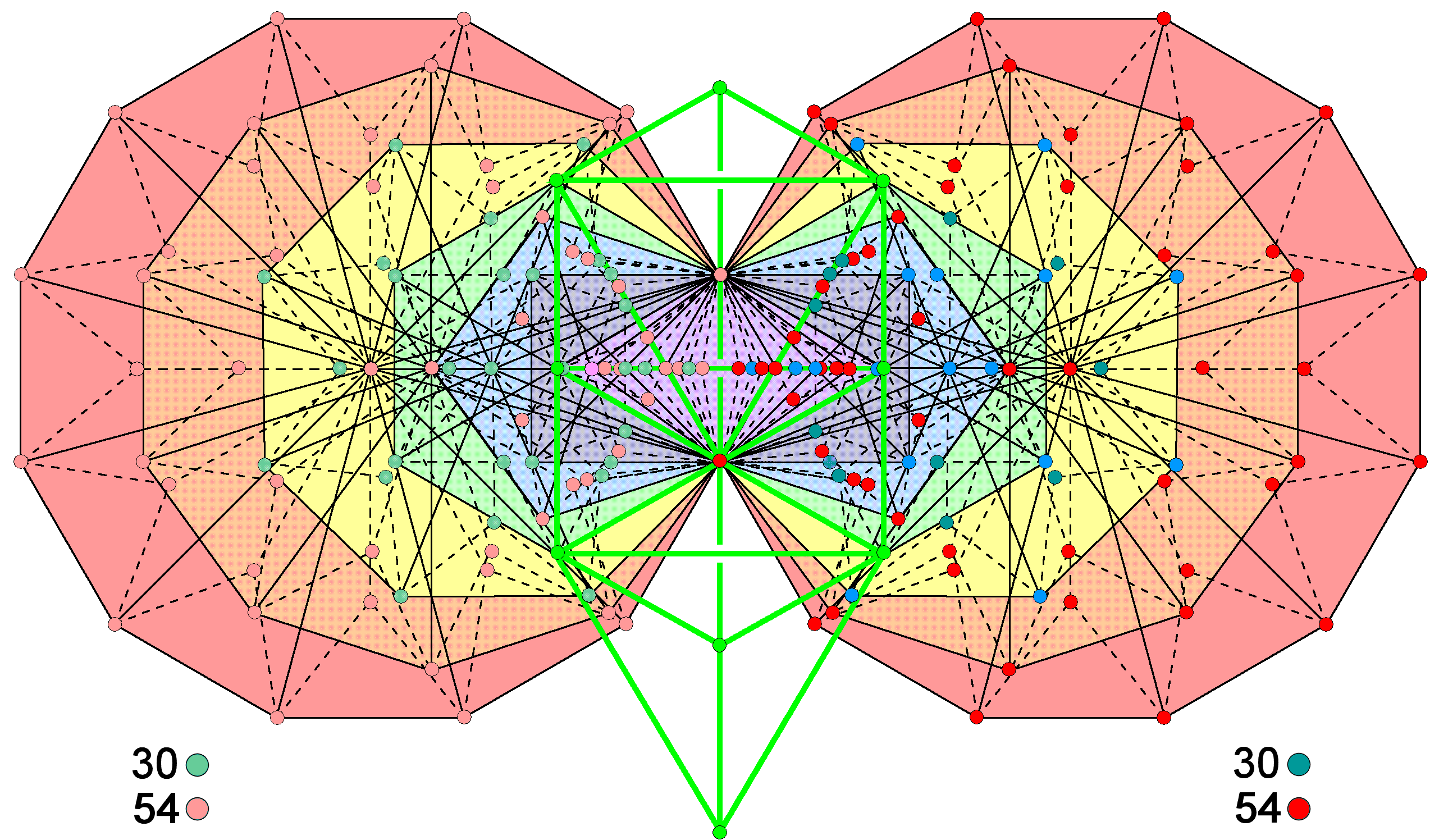
of the inner Tree of Life with Type B polygons.
| << Previous 1... 12 13 14 15 [16] Next >> |
Correspondence between the Lambda Tetractys, the outer Tree of Life
and each half of the inner Tree of Life with Type B polygons
 |
|
 |
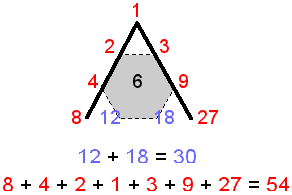
| The Lambda Tetractys. |
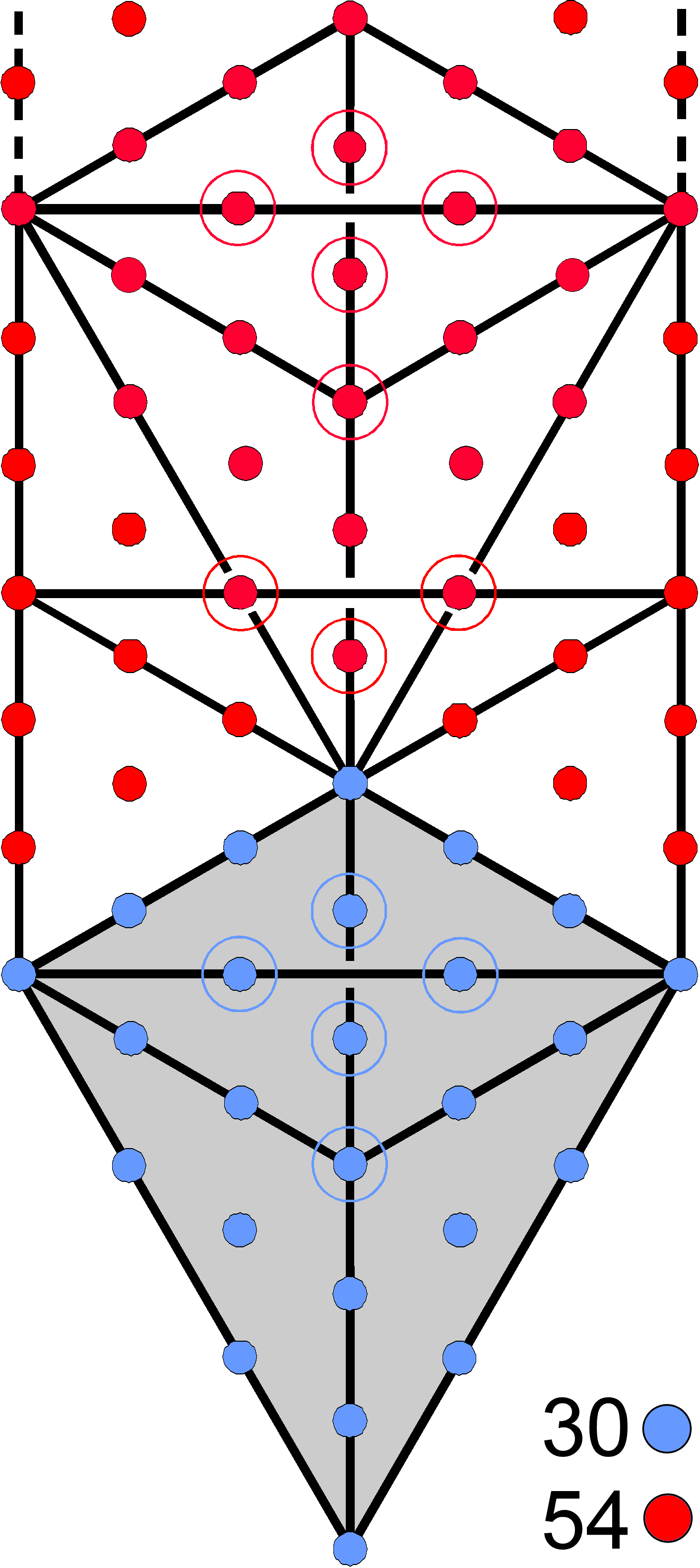
The 1-tree has 84 yods |
There are 84 corners associated with each half of the inner Tree of Life with Type B polygons. |
The Lambda Tetractys
The sum of the nine number weights surrounding the integer 6 at the centre of the Lambda Tetractys is 84. The seven
red number weights lining Plato's Lambda add up to 54:
1 + 2 + 4 + 8 + 3 + 9 + 27 = 54.
The sum of the two number weights 12 and 18 interpolated to generate the Lambda Tetractys is 30.
The 1-tree
The 1-tree is the lowest Tree in any set of overlapping Trees of Life. It has 16 triangles which, turned into
tetractyses, contain 80 yods, where 80 is the number value of Yesod, the
penultimate Sephirah of the Tree of Life. Its Lower Face is a trapezium whose corners are located at Tiphareth,
Netzach, Hod, Yesod & Malkuth. It contains 30 yods (coloured blue in the diagram shown above). Outside it are
50 red yods up to its apex. Outside the 1-tree are four red yods up to the level of its Kether.
Below this level are (30+50+4=30+54=84) yods. As the sum of seven of the nine number
weights adding to 84, the number 54 divides into 4 and 50 in two ways:
(1 + 3) + 2 + 4 + 9 + 8 + 27 = 4 + 50,
and
4 + (1 + 3 + 2 + 9 + 8 + 27) = 4 + 50.
The latter is the correct combination because the four red yods outside the 1-tree comprise two mirror-image pairs of yods, so that there is no geometric reason why they should correspond to the numbers 1 and 3.
Inner Tree of Life with Type B polygons
Just as the 1-tree contains
80 yods when its 19 triangles are tetractyses, so the (7+7) enfolded Type A polygons of
the inner Tree of Life have 94 sectors with 80 corners. When they are Type B polygons, each
sector is divided into three triangles sharing a corner, so that the (3×94=282) triangles have
(80+94=174) corners, where 282 is the gematria number value of Aralim
(Thrones), the Order of Angels assigned to Binah. When the outer & inner Trees of Life are combined, the three
green corners that lie on the central, vertica line joining the top, centre & bottom of each hexagon
coincide with the three Sephiroth on either the Pillar of Mercy or the Pillar of Judgement. That means that
(174−3−3=168) corners of the (7+7) polygons are unshared with the outer Tree of Life, i.e., they
are intrinsic to its inner form, where 168 is the gematria number value of
Cholem Yesodoth, the Mundane Chakra of Malkuth. The root edge shared by each set of seven
polygons has two ends. One corner can be associated with one set and the other can be associated with the second
set. Each set has 141 triangles with 85 corners, 84 of them being associated with either set, where
85 = 40 + 41 + 42 + 43
and
84 = 12 + 32 + 52 + 72.
The 84 corners of each set of polygons are the counterpart of the nine number weights that line the sides of the Lambda Tetractys and the 84 yods up to the level of the 1-tree. Do they exhibit a natural 30:54 division that we found above for both these systems? Tabulated below are the numbers of intrinsic corners of triangles making up the sectors of each of the seven Type B polygons:
Number of intrinsic polygonal corners outside root edge ≡ N.
Number of centres and corners inside polygons ≡ n.
Number of intrinsic corners associated with each set of 7 enfolded Type B polygons
|
|
Root edge |
Triangle |
Square |
Pentagon |
Hexagon |
Octagon |
Decagon |
Dodecagon |
Total |
|
N |
1 |
0 |
2 |
3 |
2 |
6 |
8 |
10 |
32 |
|
n |
0 |
3 + 1 = 4 | 4 + 1 = 5 | 5 + 1 = 6 |
5 + 0 = 5 |
8 + 1 = 9 |
10 + 0 = 10 |
12 + 1 = 13 |
52 |
|
Total |
1 |
4 |
7 |
9 |
7 |
15 |
18 |
23 |
84 |
Associated with each set are 32 polygonal corners and 52 inernal corners & centres. We see that the required division is not that between polygonal and internal corners. However, there are three ways of choosing numbers in the "Total" row whose sum is 30:
Only the first and third possibilities allow for the four red yods outside the 1-tree to correspond to the number weight 4. The third diagram shown above depicts the latter possibility. On the other hand, it can be argued that the 54 corners should include the associated end of the root edge, i.e., "1", because, in the context of the seven number weights lining the Lambda Tetractys whose sum is 54, the number 54 includes the number weight 1, which corresponds, intuitively speaking, to this corner, in which case the first possibility is the correct one. The crucial issue here, however, is not the ambiguity in choice of polygons — a problem which need not be solved at this moment. Instead, it is the fact that the 30:54 division does, indeed, exist in a natural way for the 84 corners associated with each half of the inner Tree of Life, just as it does in the Lambda Tetractys. We should expect this because they are both representations of the archetypal holistic pattern and any significant subpattern in one must have its counterpart in the other.
As discussed in #8 of this section, the Tetrad Principle determines the holistic pattern of the Lambda Tetractys because the sum of its 10 number weights is 90, which is the number of yods outside the root edge of the first four enfolded Type A polygons that belong to the inner Tree of Life. It also picks out the hexagon (the fourth of these polygons) as the single polygonal representation of the Lambda Tetractys because 90 yods surround its centre when it is Type B:
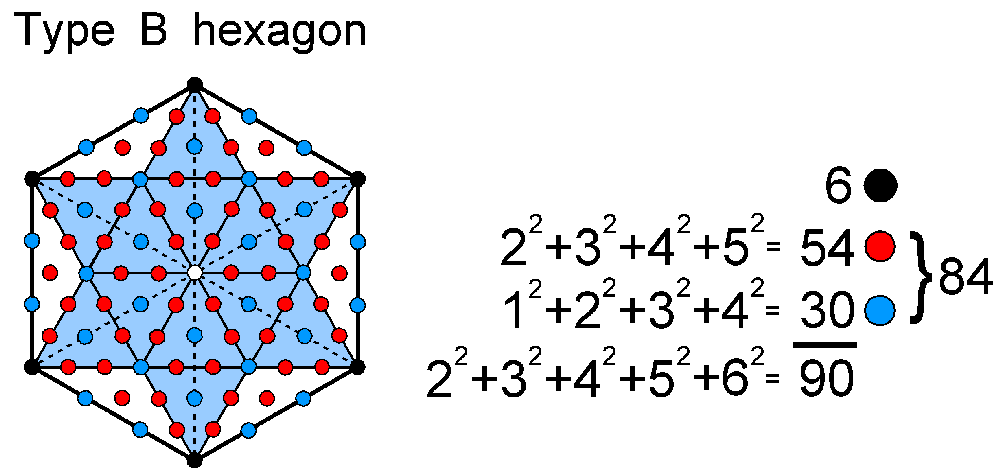
The 30 blue yods other than the black corner yods of the Type A hexagon that surround its centre correspond to the 30 corners associated with (taking the third possible combination listed above) the square, hexagon & octagon. The 54 red yods added by changing the hexagon from Type A to Type B correspond to the 54 corners in the triangle, pentagon, decagon & dodecagon.
The Tetrad Principle also determines in an arithmetic way both the sum (84) of the nine number weights lining the Lambda Tetractys and their 30:54 division. As
91 = 12 + 22 + 32 + 42 + 52 + 62,
90 = 22 + 32 + 42 + 52 + 62.
As
55 = 12 + 22 + 32 + 42 + 52,
54 = 55 − 1 = 22 + 32 + 42 + 52.
whilst
30 = 12 + 22 + 32 + 42.
We see that 30 is the sum of the squares of the first four integers, starting with 1, and that 54 is the sum of the squares of the first four integers after 1. Their sum is 84, which is the sum of the squares of the first four odd integers:
84 = 12 + 32 + 52 + 72.
| << Previous 1... 12 13 14 15 [16] Next >> |