
| << Previous 1... 4 5 [6] 7 8 ...39 Next >> |
#6 The decagon with 2nd-order tetractyses & the 7 separate Type B polygons have 720 yods

A decagon whose sectors are 2nd-order tetractyses has 620 hexagonal yods and 101 corners of 100 tetractyses, where 101 is the 26th prime number and the number value of Michael, the Archangel of Tiphareth. 720 yods surround its centre, where
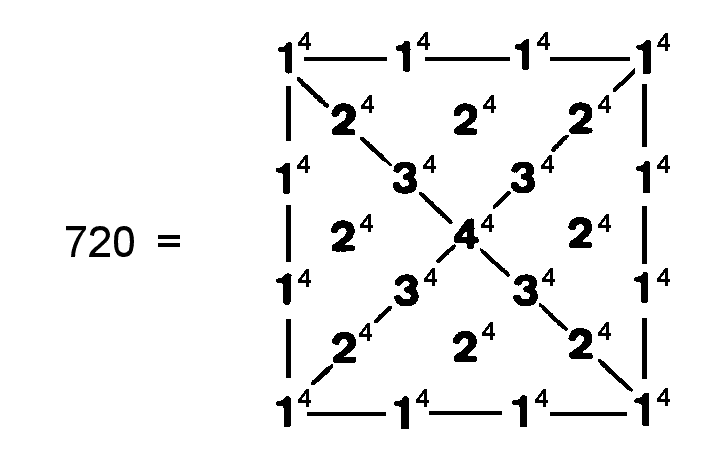
It shows how the Tetrad, symbolized by the square, expresses this number. The number of yods in an n-sided, Type B polygon = 15n + 1, where 15 is the number value of YAH. The seven regular, Type B polygons with 48 sides have (48×15=720) yods surrounding their centres. We see, therefore, that the Decad (10), which is symbolized by the decagon, determines how many yods are needed to construct the seven separate polygons of the inner Tree of Life, starting from their centres. Enfolded, the seven polygons have 687 yods, so that (727−687=40) yods disappear when all the polygons become enfolded, where 40 = 4(1+2+3+4) = 4 + 8 + 12 + 16, i.e., the sum of the first four integers that start with 4 and which are four units apart.
| << Previous 1... 4 5 [6] 7 8 ...39 Next >> |