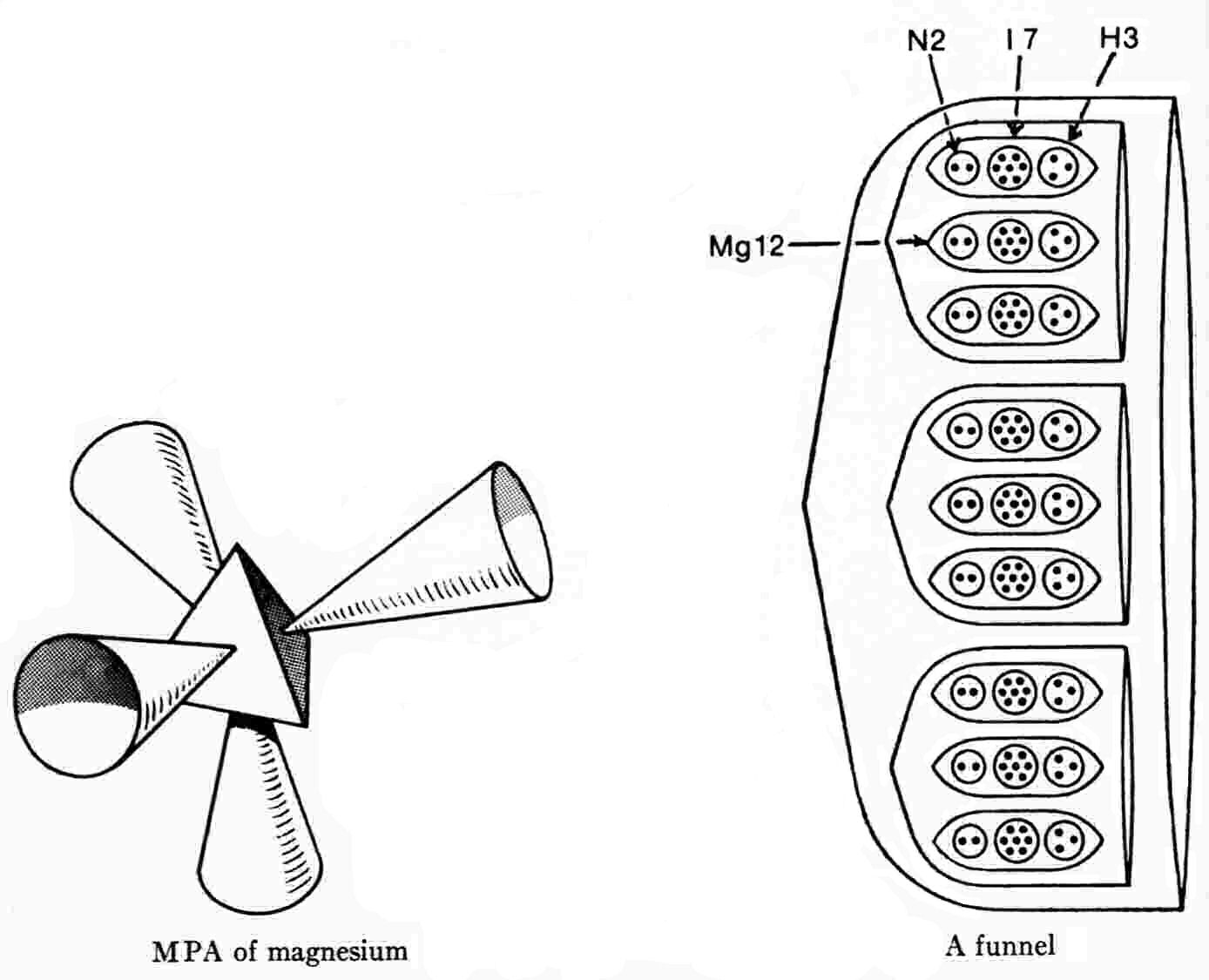
The Magnesium MPA
The magnesium MPA is a tetrahedral array of four similar funnels, Each funnel contains three identical segments, each containing three similar ovoids (Mg12) enclosing twelve UPAs. An Mg12 group is made up of three spheres enclosing two UPAs (N2), seven UPAs (I7) and three UPAs (H3).
Magnesium MPA =
4[3(3Mg12)].


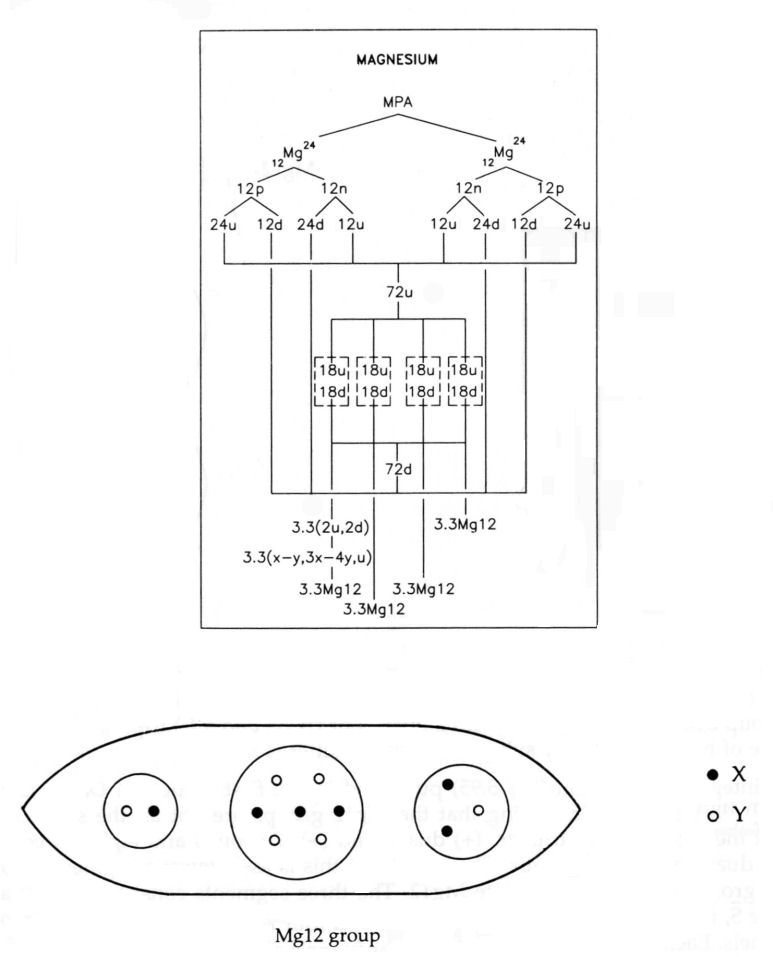
The MPA is formed from two Mg12 nuclei, which provide 432 subquarks — the same number as the number of UPAs. The 108 subquarks in eight u and eight d quarks are present in each funnel, each Mg12 containing the twelve subquarks in two u and d quarks. The N2 is an X-Y bound state, the I7 is a bound state of three X and four Y subquarks (actually the mirror state I7′ of the I7 group found in the iodine MPA) and the H3 is a u quark:
Mg12 = N2 + I7 + H3
= X-Y + 3X-4Y + + u.
(see diagram below). The disintegration diagram confirms that the H3 in the Mg12 group is a (+) triplet, i.e., a u quark, and that the N2 is a (0) duad, i.e., an X-Y bound state. The I7 group dissociates at stage E2 into a quartet of UPAs and a (−) triplet. The former is a bound state of two X and two Y subquarks and the latter is a d quark:
3X-4Y → 2X-2Y + d (= 2Y-X).
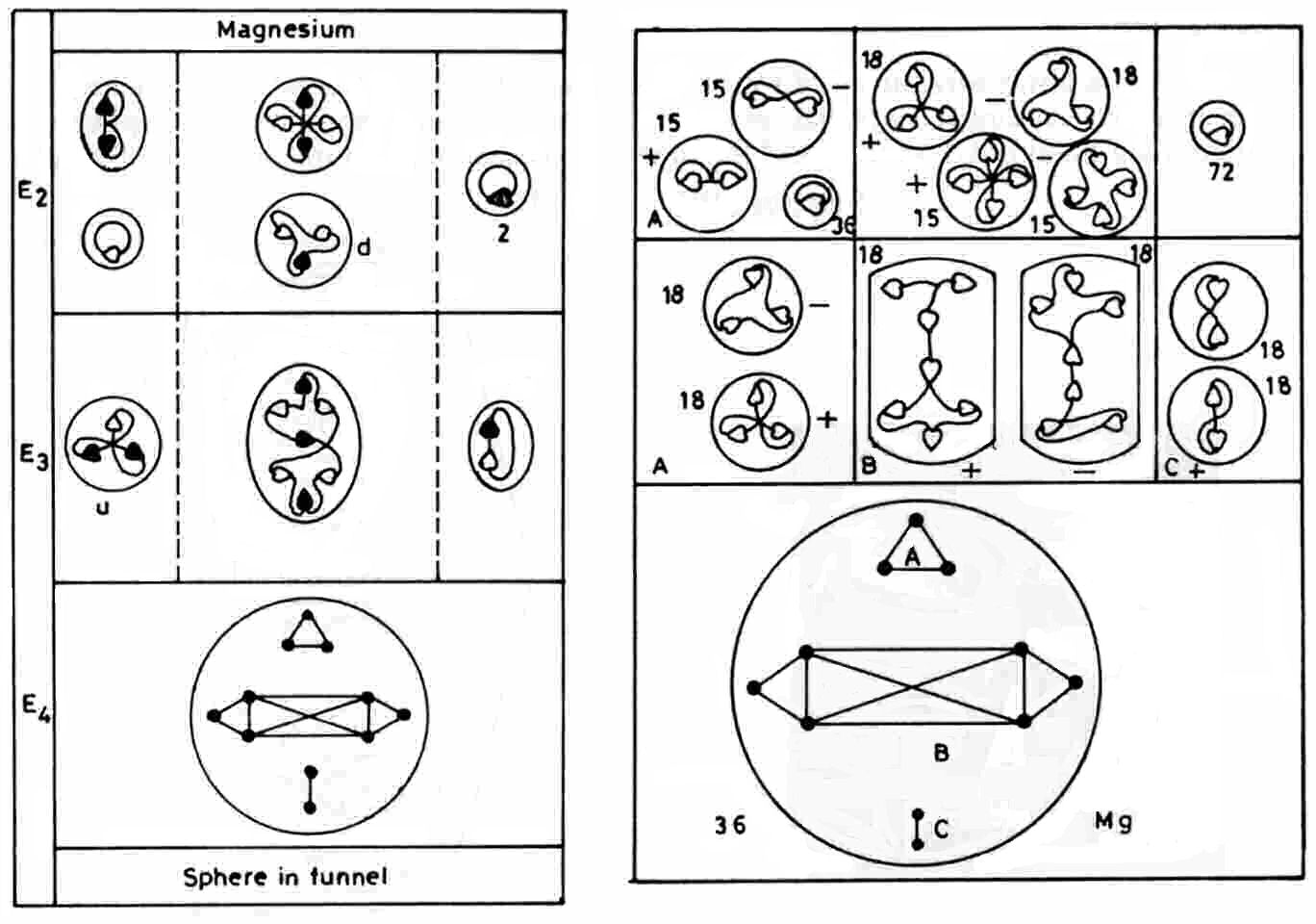
The disintegration diagram published in the first edition of Occult Chemistry is shown above on the right. It differs from that in the third edition by indicating that the Mg12 groups are not all the same. Instead, eighteen of them contain (+) triplets, (+) duads and (+) I7 groups and eighteen contain (−) triplets, (−) duads and (−) I7 groups. This reason for this is as follows: a segment S contains two Mg12 groups and its mirror state Mg12′. The three segments consist of two S and its mirror state S′, i.e., five Mg12 groups and four Mg12′ groups. This is the composition of each of two funnels. Each of the two other funnels contains the mirror states of the former, i.e., two S′ and one S, or five Mg12′ groups and four Mg12 groups. The composition of the MPA is:
2(5Mg12 + 4Mg12′) + 2(5Mg12′ + 4Mg12) = 18Mg12 + 18Mg12′,
where
Mg12 = X-X + 6X-Y + u
and
Mg12′ = Y-Y + 6Y-X + d.
The (+) I7 group shown in the disintegration diagram of the first edition is a 6X-Y bound state and the (−) I7 (its mirror state I7′) is an X-6Y bound state. This predicted composition is confirmed by the fact that the (+) I7 group releases a (+) quartet of UPAs (4X) and a (+) triplet (u quark), whilst the (−) I7 releases a (−) quartet (4Y) and a (−) triplet (d quark) consistent with their predicted subquark compositions:
6X-Y → 4X + u (= 2X-Y)
and
6Y-X → 4Y + d (=2Y-X).
The prediction that the I7 groups described for the magnesium MPA in the first edition of Occult Chemistry do, indeed, differ in composition from those depicted in the third edition is supported by the fact that the configurations of the strings binding together their UPAs are quite dissimilar. The particles in two funnels are mirror states of their counterparts in the two other funnels. What makes this possible is the fact that the Mg12 nucleus is made up of an equal number of protons and their mirror states — neutrons, i.e., the same number of X and Y subquarks. The magnesium MPA is another example of what the author has called "edition variants," previously encountered in the analysis of the oxygen MPA. The third edition variant was presumably recorded in a second examination of the magnesium MPA years after it was first described in the first edition. The importance of such variants is that — given that in each case they were formed from two nuclei of the same isotope because they contain the same number of UPAs — the total numbers of X and Y subquarks in their constituent particles implied by their slightly different disintegration diagrams should still be the same, despite breaking up into different particles. This means that they pose an additional test of consistent with theory. The analysis of the magnesium MPA therefore provides a remarkable example of a perfect consistency between theoretical demands and the types of particles reported to make up MPAs. The notion that such consistency — in addition to the agreement between theory and observation for the third edition variant — could also be the result of chance is plainly ludicrous, given the large set of details that the theory explains.