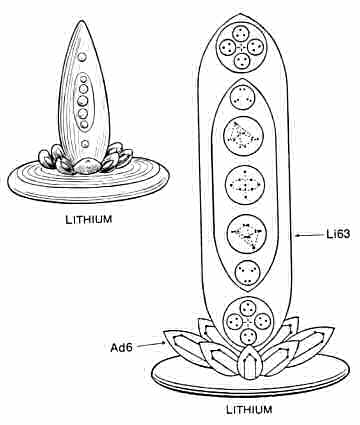
The Lithium MPA
The lithium MPA consists of a central, spike-shaped aggregate of particles, at the base of which is a globe containing four spheres, each enclosing a tetrahedral array of four UPAs (Li4). Eight Ad6 groups radiate like petals from the globe. The spike formation revolves rapidly on its axis, carrying these groups with it. The spike (Li63) contains sixty-three UPAs in two globes and a long ovoid. The four spheres containing H3 triplets within each globe revolve as a cross. Within the ovoid are five spheres, one at each end enclosing three duads of UPAs, two enclosing groups of nine UPAs and the central one having an axis of three UPAs surrounded by a spinning wheel of six UPAs.
Lithium MPA = 4Li4 + Li63 + 8Ad6.
|
|
|
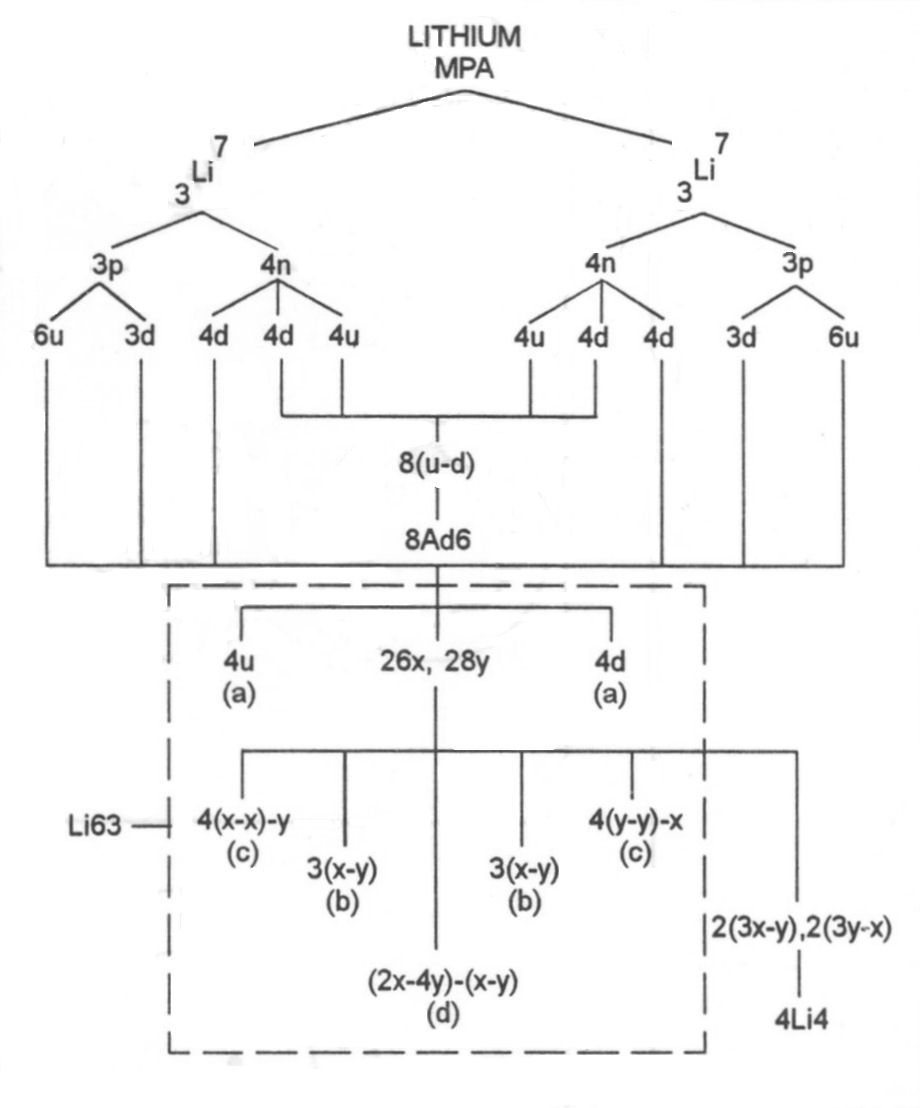
The lithium MPA is formed from two Li7 nuclei, which provide 126 subquarks — one fewer than the number of UPAs. One less UPA is predicted to be in the Li63 group — in particular, because of the mirror symmetry of the arrangements of its particles — in the central sphere, where two, not three, UPAs should comprise the axis. The four neutrons in each lithium nucleus provide eight u-d diquarks as the Ad6 petals. This is confirmed by the disintegration diagram below, which shows that the eight Ad6 groups break up at the E2 stage into eight (+) triplets (u quarks) and eight (−) triplets (d quarks), i.e., each Ad6 is a u-d diquark. The subquarks in the remaining twelve u quarks and fourteen d quarks make up the central globe and Li63 spike. The four Li4 groups consist of two 3X-Y bound states and two X-3Y bound states — the mirror state Li4′. This prediction cannot be checked because, unfortunately, the Li4 groups were not further broken up into duads of UPAs. Analysis of the fluorine MPA and many other MPAs will, however, reveal that the tetrahedral Li4 group can dissociate into a (+) duad (X-X) and a (0) duad (X-Y), which is consistent with its predicted composition:
3X-Y → X-X + X-Y.
The four triplets at one end of the spike are u quarks; the four triplets at the other end are d
quarks. The disintegration diagram confirms that one sphere (a) breaks up at stage E2 into four (+) triplets (u
quarks) and the other sphere (a) breaks up into four (−) triplets (d quarks). The duads in the sphere inside the
Li63 at each end are X-Y bound states. The disintegration diagram confirms this by indicating that the two groups b
break up into six (0) duads, i.e., six X-Y bound states. One group (c) is four X-X bound states bound to
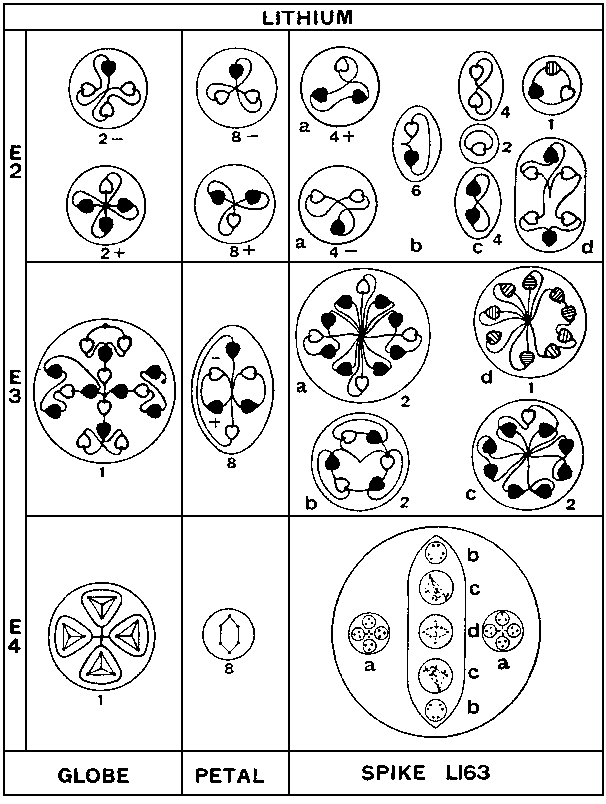a nucleus of one Y subquark, the other is four Y-Y bound states bound to a nucleus of one X
subquark. This is confirmed by the fact that, according to the disintegration diagram, one group (c) breaks up
at the E2 stage into four (+) duads (X-X) and a free UPA, whilst the other one breaks up into four (−) duads
(Y-Y) and a free UPA. Group d consists of two X subquarks and four Y subquarks revolving in a common orbit
around an X-Y bound state, not the reported three UPAs. This prediction cannot be tested because group d broke
up into two particles whose quark/subquark composition is not deducible as they were not broken up further
into triplets or duads of UPAs. The Li63 group should contain sixty-two, not sixty-three, UPAs. It has the
subquark composition:
Li63 = 30X + 32Y.
The group also appears in the MPAs of potassium, manganese, rubidium, technetium, caesium, barium, promethium, thulium, rhenium, francium, radium, actinium, thorium and uranium, making it in principle a powerful test of consistency of analysis, although its effectiveness is somewhat reduced by the fact that most of these elements have no disintegration diagrams to permit a complete comparison between the types of particles making up their MPAs and the theory that these particles originated in the protons and neutrons making up two of their atomic nuclei.
