| << Previous 1 [2] 3 4 Next >> |

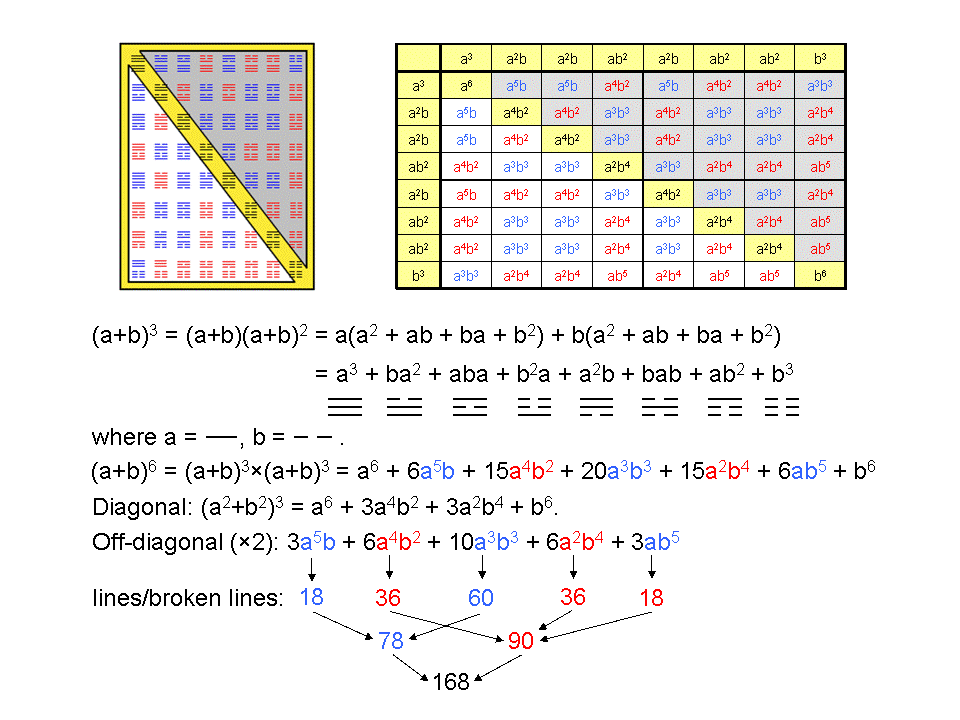
If a line — and broken line – – are represented by the algebraic symbols "a" and "b" and non-commutivity of their multiplication is assumed, i.e., ab ≠ ba, the eight trigrams express the eight possible terms in the cubic expansion of (a+b)3. The 64 hexagrams express the 64 possible terms in the expansion of (a+b)6 = (a+b)3×(a+b)3. The conclusion of the analysis presented here does not depend on assuming non-commutivity, so let us drop this assumption for convenience. The eight diagonal hexagrams symbolize the eight terms in the expansion of (a2+b2)3. Terms that correspond to off-diagonal hexagrams that contain even powers of a and b are written in red; their counterpart hexagrams are likewise coloured. Terms with odd powers of a and b are written in blue; they correspond to blue off-diagonal hexagrams. In each off-diagonal half of the I Ching table, there are three blue hexagrams symbolizing the term a5b, six red hexagrams symbolizing the term a4b2, 10 blue hexagrams symbolizing the term a3b3, six red hexagrams symbolizing the term a2b4 and three blue hexagrams symbolizing the term ab5. The 168 lines & broken lines comprise 78 lines & broken lines that symbolize the terms a5b and a3b3 and 90 lines & broken lines that symbolize the terms a4b2, a2b4 & ab5. There is ambiguity here whether the term a5b or ab5 is to be associated with the 78 lines & broken lines because each corresponds to 18 lines & broken lines. This means that there are two possible ways of identifying the sets of 78 and 90 lines & broken lines. But which one is correct does not matter as far as the conclusion to be made here is concerned. Whichever choice is made results in the same two numbers.
| << Previous 1 [2] 3 4 Next >> |