Human skeleton Part 4

<< Previous 1... 2 3 [4] 5 6 ...15 Next >>

#4 The inner form of the 3-tree encodes the human skeleton

The inner form of the Tree of Life (Fig. 5) is discussed in Sacred geometry/Tree of Life. Its 14 enfolded regular polygons have 70 corners. Each overlapping Tree of Life has its own similar inner form, so that the inner form of the lowest n Trees of Life consists of 14n enfolded polygons with C(n) = 68n + 2 corners, the number "2" here denoting the highest corners of the two hexagons enfolded in the nth Tree of Life. The ten spatial dimensions of 11-dimensional space-time are prescribed by ADONAI, the Godname of


Figure 5. The inner Tree of Life.	Figure 6. The inner form of the 3-tree.

Malkuth, because they are mapped by 10 overlapping Trees of Life with 65 emanations, and 65 is the number value of this Godname. The three lowest Trees of Life map the three large-scale dimensions of space and the next seven Trees map the seven compactified dimensions of the 11-dimensional space-time predicted by M-theory. As the representation of Adam Kadmon (the divine prototype), the Tree of Life can be replaced by 10 Trees of Life, each representing a Sephirah. The lowest three of these Trees map the three-dimensional aspect of Heavenly Man, that is, his physical body. Their inner form consists of 42 regular polygons with C(3) = 206 corners. As geometrical degrees of freedom, these corners denote the 206 bones making up the 3-dimensional, human skeleton.

Equivalence of human skeleton and inner form of 3-tree

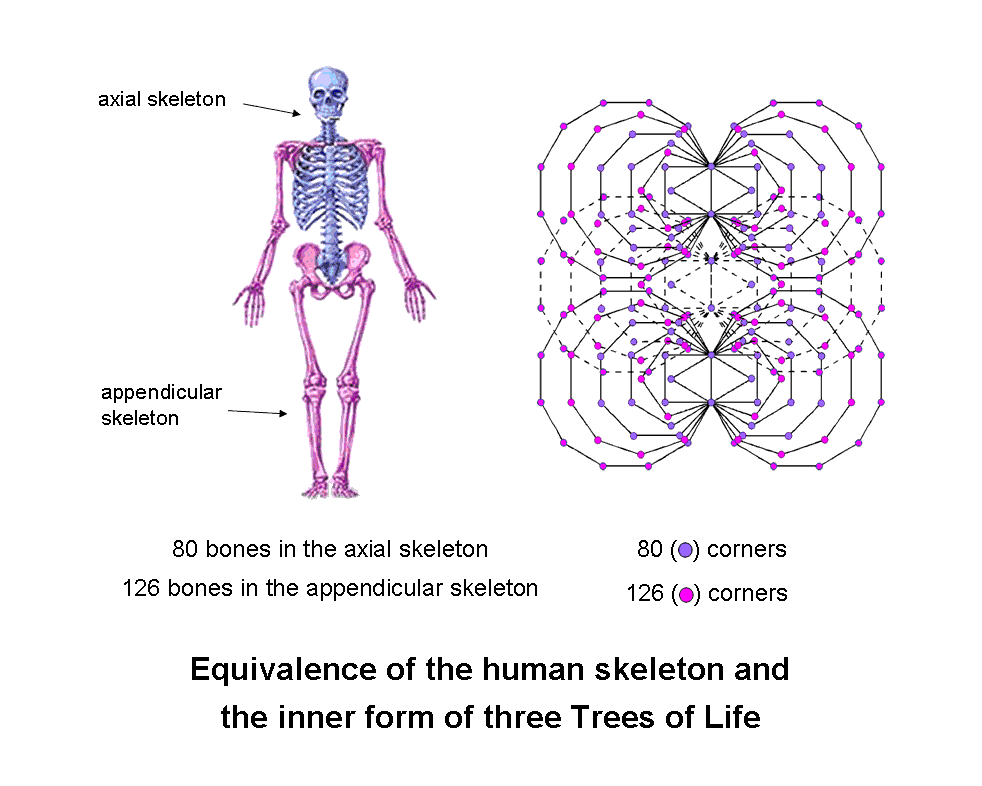It is possible (at least to some degree) to differentiate which polygons refer to the 80 bones of the axial skeleton and which refer to the 126 bones of the appendicular skeleton, as the following argument shows: as 80 is not exactly divisible by 3, but 126 is such, the 80 corners cannot belong to three similar, complete subsets of polygons unless the latter include the two hexagons. This is because the hexagons in adjacent Trees of Life share some of their corners, so that they are the only polygons whose numbers of corners for the complete set of 42 polygons is not a multiple of 3 (the six hexagons have 26 corners, 20 of which lie outside the three root edges; neither number is exactly divisible by 3). Hence, the set of polygons with 80 corners must include the hexagons. Figure 7 displays a possible assignment.* The 80 purple corners denoting bones in the axial skeleton are either corners of octagons and squares or corners of triangles and hexagons that coincide with Sephirothic emanations of the 3-tree. The 126 pink corners denote the 126 bones in the appendicular skeleton. It should be noted that this assignment is not the only possible one (see footnote). However, it does have the intuitively attractive feature that 14 of the 80 dots coincide with emanations of the 3-tree, which should be compared with the fact that there are 14 facial bones in the axial skeleton (see #3). This is reinforced by the following facts:

1. given that the set of 14 corners includes the top and bottom of each hexagon, its remaining corners are either the endpoints of the three root edges or the outer corners of the triangles; only the latter coincide with Sephiroth;

2. the 14 corners that are Sephiroth of the 3-tree comprise six pairs, each pair being located on the left and right pillars, and a pair located at Chokmah and Binah of the third Tree, which coincide with the topmost corners of the two hexagons enfolded in this Tree. Compare this with the 14 facial bones comprising six pairs of bones: maxillae, zygomatic, nasal, platine, inferior nasal concha & lacrimal, and two unpaired bones: mandible & vomer (see YouTube video).

It is implausible that the existence of this 2×(6+1) pattern in the 14 shared corners is a coincidence. Rather, it is simply a manifestation of the exact isomorphism between the types of bones in the human skeleton and the types of corners in the 42 polygons making up the inner form of the 3-tree.

Figure 7

14 shared corners symbolise 14 facial bones

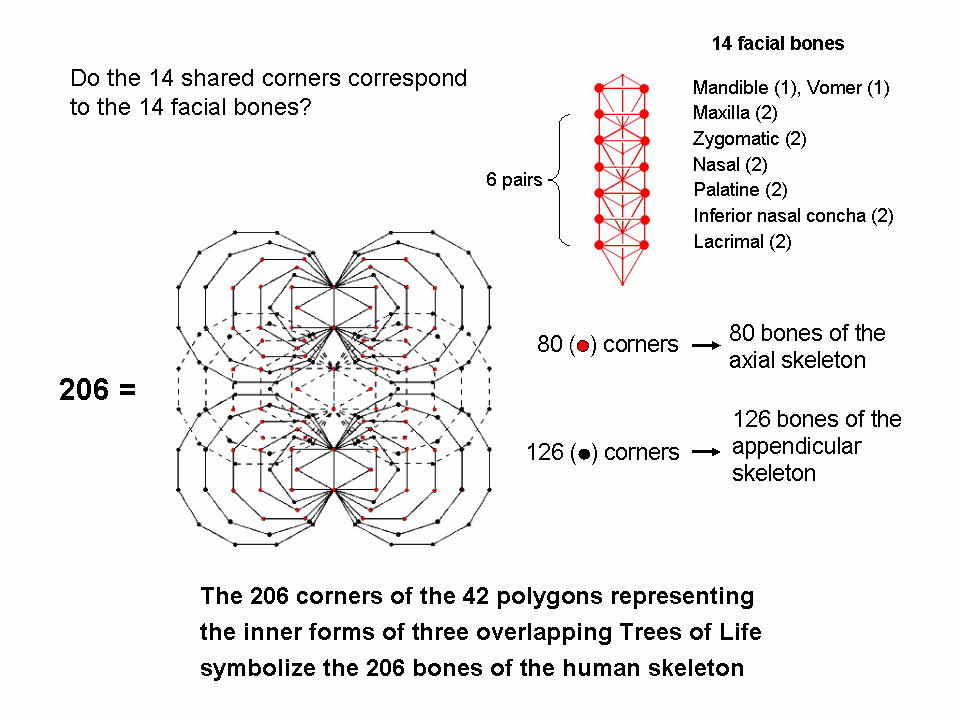Figure 8. The 14 corners (red dots in the 3-tree) of the triangles & hexagons that coincide with Sephirothic emanations of the 3-tree symbolize the 14 bones in the human face. The lowest 6 pairs of corners correspond to the 6 pairs of facial bones and the highest pair of corners correspond to the two unpaired facial bones.

The six corners coinciding with Sephiroth in each side pillar denote the six bones on either side of the face; the topmost corners of the two hexagons enfolded in the third Tree of Life denote the mandible and vomer — the two single, unpaired, facial bones.

The 80 bones in the axial skeleton may now be written:

80 = 14 + 66,

where 14 is the set of 14 facial bones and 66 is the remainder of the axial skeleton. As 14 = 2(1) + 6(2) and 80 = 34(1) + 23(2),

66 = 32(1) + 17(2).

The 66 non-facial bones of the axial skeleton comprise (32+17=49) types prescribed by EL CHAI, the Godname of Yesod with number value 49. The number 66 is the 65th integer after 1, where 65 is the number of ADONAI, the Godname of Malkuth. They include 26 vertebrae, where 26 is the number value of YAHWEH, the Godname of Chokmah, and 32 single bones, where 32 is the 31st integer after 1 and 31 is the number value of EL, the Godname of Chesed, the Sephirah immediately below Chokmah on the Pillar of Mercy. The number 66 is divisible exactly by 3, but neither the number 32 nor the number 17 is such. This means that each of the three sets of polygons whose corners number 66 cannot express the same number of single bones and the same number of paired bones. The simplest way of restoring this property is to assign two single bones and two pairs of bones to the six endpoints of the three root edges, leaving 30 single bones and 15 pairs of bones. They can be assigned to the remaining 60 corners in a variety of ways. However, the assignment mentioned above, in which the 80 bones are assigned to the corners of dodecagons and corners coinciding with emanations, leads to the 30 corners outside the root edges of one set of three dodecagons symbolizing the 30 single bones and the 30 corners of the other set of three dodecagons symbolizing the 30 bones that are paired. Hence, there is a unique assignment in which the distinction between bones that occur singly and in pairs has a geometrical counterpart. As

66 = 8 + 6 + 1 + 26 + 25,

where 8 = 4(1) + 2(2), 6 = 3(2), 1 = 1(1), 26 = 26(1) and 25 = 1(1) + 12(2), the 66 bones do contain two single bones from the various groups in the axial skeleton that occur on their own, namely, the hyoid and sternum, as well as two pairs of bones that likewise occur on their own, namely, the parietal and temporal bones in the cranium. Because of this distinction, there is nothing ad hoc in their assignment to the endpoints of the three root edges.

* If the intuitively reasonable assumption is made that the bones corresponding to the two endpoints of each root edge must belong to the axial skeleton, the only alternative to the illustrated assignment can be deduced as follows: because they include the hexagons, the 80 corners of the 42 polygons are given by

80 = 3×26 + 2,

where 26 is the number of corners per set of 14 polygons. If these include the root edge, 26 = 8 + 18, where the former number is the number of corners of the two hexagons per set and the latter is the number of corners of the other set of polygons outside the root edge (nine in each set of polygons and nine in their mirror images). The numbers of corners of each polygon outside the root edge are:

Polygon	triangle	square	pentagon	hexagon	octagon	decagon	dodecagon
Numbers of corners outside root edge	1	2	3	4	6	8	10

Either:
1. a triangle & decagon,
2. a pentagon & octagon,
3. a triangle, square & octagon
have nine such corners. Combination 2 is excluded if the intuitively reasonable assumption is made that corners shared with the outer Tree of Life ought to denote bones of the axial skeleton rather than bones of the appendicular skeleton, for the corner of the triangle that lies outside its root edge is just such a shared corner, but none of the corners of the pentagon and octagon are shared. We conclude that there are only two schemes of correspondence between corners and bones of the axial skeleton that are intuitively plausible. Its 80 bones correspond to the 80 corners of the triangles, hexagons and either the squares & octagons or the decagons. Figure 8 depicts the former scheme of correspondence.

<< Previous 1... 2 3 [4] 5 6 ...15 Next >>

Home