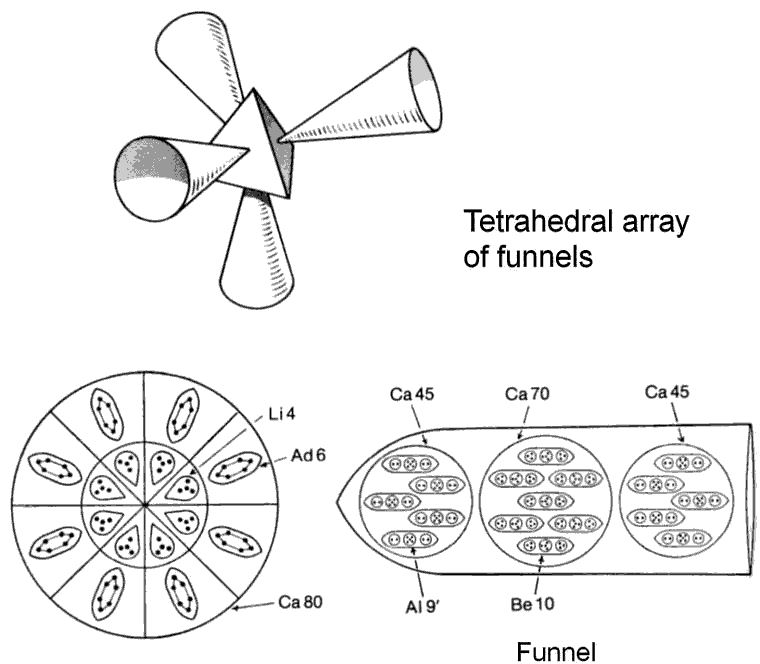
The Calcium MPA

The calcium MPA consists of a central globe (Ca80), from which four funnels project in a tetrahedral array. The Ca80 globe is a pair of concentric spheres, both of which are divided into eight equal segments. Each segment in the inner sphere contains a tetrahedral Li4 group; each outer sphere encloses a cigar-shaped Ad6 group. Each funnel contains 160 UPAs in three spheres (Ca160), the central one (Ca70) enclosing seven Be10 ovoids and the two spheres (Ca45) on either side each containing five Al9′ ovoids (NB: here, an Al9′ is not the mirror state of Al9 but a group of nine UPAs labelled as such in Occult Chemistry by Besant & Leadbeater).

Calcium MPA = (8Li4 + 8Ad6) + 4(5Al9′ + 7Be10 + 5Al9′)

                                           = Ca80 + 4(Ca45 + Ca70 + Ca45)

                                           = Ca80 + 4Ca160.

The calcium MPA is formed from two Ca⁴⁰ nuclei, which provide 720 subquarks — the same as the number of UPAs. The eight Ca45 groups are made up of subquarks belonging to the twenty protons in one Ca⁴⁰ nucleus and to the twenty neutrons in the other Ca⁴⁰ nucleus. In one Ca45 group, each Al9′ 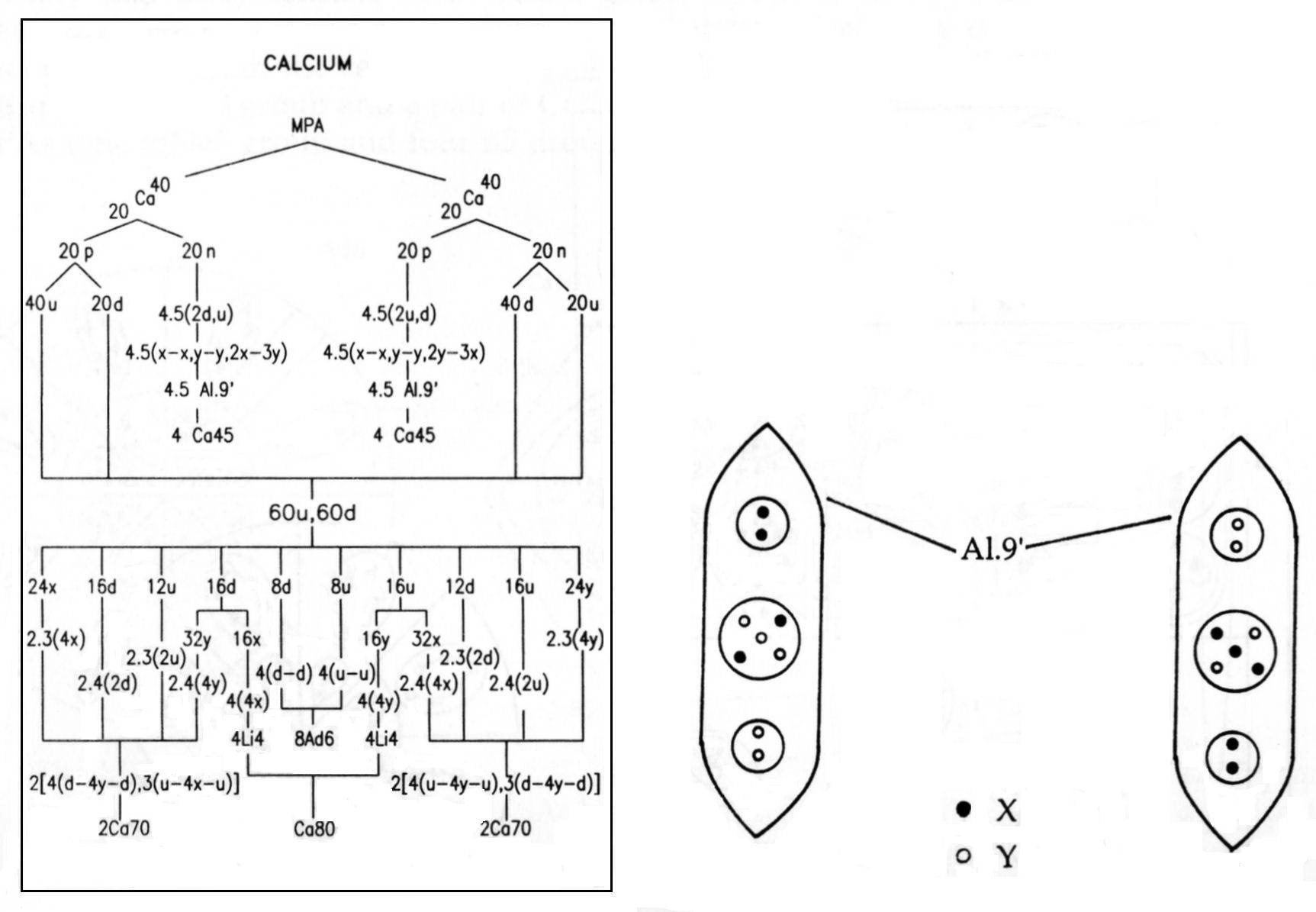group comprises the subquarks in a proton that, having been set free, recombined into X-X and Y-Y bound states and a square pyramidal array of three X subquarks and two Y subquarks:

proton (= 5X-4Y) → X-X + Y-Y +3X-2Y.

In the other Ca45 group, each Al9′ group is made up of the subquarks released from a neutron that recombined into Y-Y and X-X bound states and a square pyramidal array of three Y subquarks and two X subquarks:

neutron (= 4X-5Y) → Y-Y + X-X + 3Y-2X.

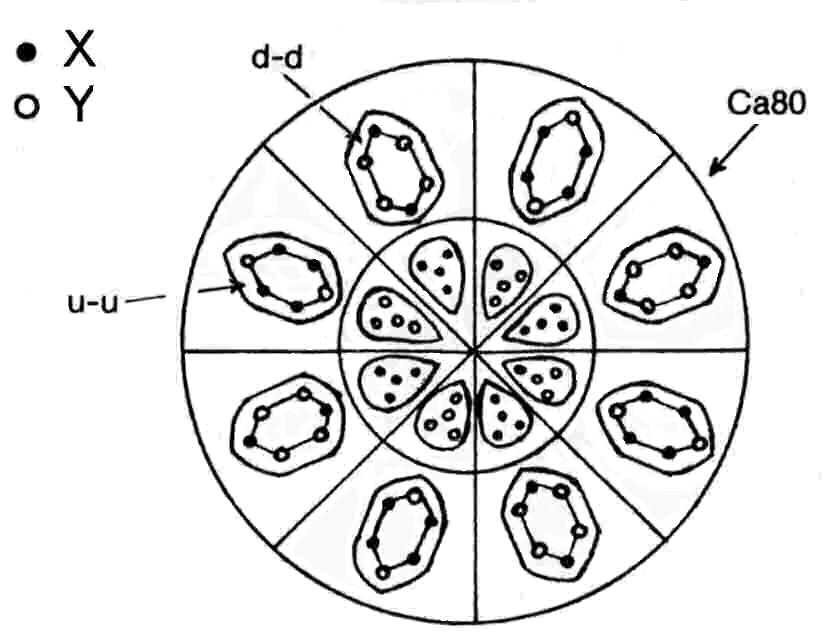
The two Ca45 groups are therefore mirror states of each other. The disintegration diagram shown below confirms the prediction that the pair of Ca45 groups contains ten (+) duads (X-X) and ten (−) duads (Y-Y) because, among the products of disintegration of these two groups at stage E3 are ten (+) duads and ten (−) duads. Four of the Ad6 groups in the Ca80 are u-u diquarks; the other four Ad6 groups are d-d diquarks, i.e., their mirror particles. Four Li4 groups in its central sphere are bound states of four X subquarks; the other four Li4 groups are bound states of four Y subquarks, i.e., the mirror state Li4′ of the former. Four segments of the larger sphere enclose a u-u diquark and a tetrahedral cluster of four X subquarks; four segments contain a d-d diquark and a cluster of four Y subquarks. The disintegration confirms this composition because it shows that the globe breaks up at stage E3 into:

1. four (+) Ad6 groups, each of which splits up at stage E2 into two (+) triplets, i.e., u quarks;
2. four (−) Ad6 groups, each of which breaks up into two (−) triplets (d quarks);
3. four (+) Li4 groups, which split up at stage E2 into eight (+) duads, or X-X bound states;
4. four (−) Li4 groups, which break up into eight (−) duads, or Y-Y bound states.

The composition of the Ca70 group is shown below:

2 funnels: Be10 (×4): u-4X-u;
                 Be10 (×3): d-4Y-d;
2 funnels: Be10′ (×4): d-4Y-d;
                 Be10′ (×3): u-4X-u;

The disintegration diagram confirms this because it shows that there are four Be10 groups made up of two (+) triplets (u quarks) and one (+) Be4 group (4X) and three Be10 groups, each with two (−) triplets (d quarks) and one (−) Be4 group (4Y). The compositions of these two types of Be10 groups agree with what was found for the (+) and (−) Be10 groups in the analysis of the beryllium MPA.

 Every particle in the calcium MPA both agrees with theoretical prediction and is consistent with results of analysis of other MPAs. There is no alternative, plausible explanation for such spectacular, detailed agreement than that the MPA of an element is formed from two of its atomic nuclei and that Besant & Leadbeater were able to remote-view its constituent multi-quark and multi-subquark bound states.

Home