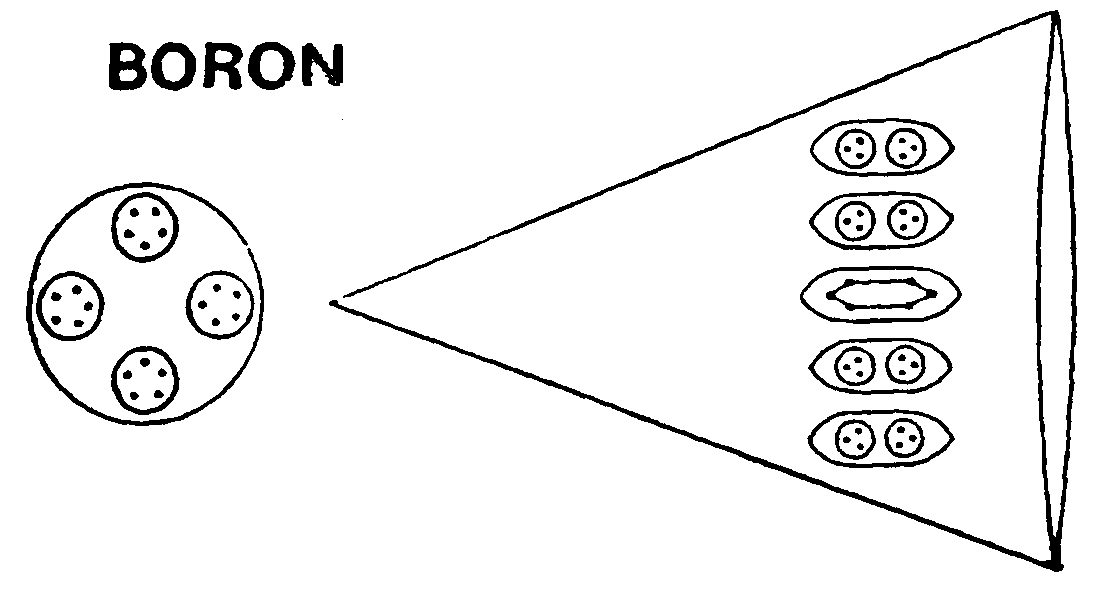
Central globe & a funnel of the boron MPA.The Boron MPA
The boron MPA is a face-centred cubic array of six funnels projecting from a central globe. A funnel contains an Ad6 group and four ovoids, each of which contains two hydrogen triplets (H3). The globe has four spheres, each enclosing groups of five UPAs (B5).
Boron MPA = 4B5 + 6[4(((2H3) + Ad6].
Central globe & a funnel of the boron MPA.
The MPA is formed from two B11 nuclei, which provide 198 subquarks, i.e., two
fewer than the number of UPAs. The twenty-four d quarks present in the twelve neutrons of both nuclei are the pairs
of triplets in two ovoids in each funnel, the two other ovoids containing pairs of u quarks. These quark pairs are
not diquarks because the quarks are bound not by strings but by the residual coupling between the strings binding
their subquarks; they are the quark counterpart of the deuteron. That u and d quarks make up the ovoids is
confirmed by the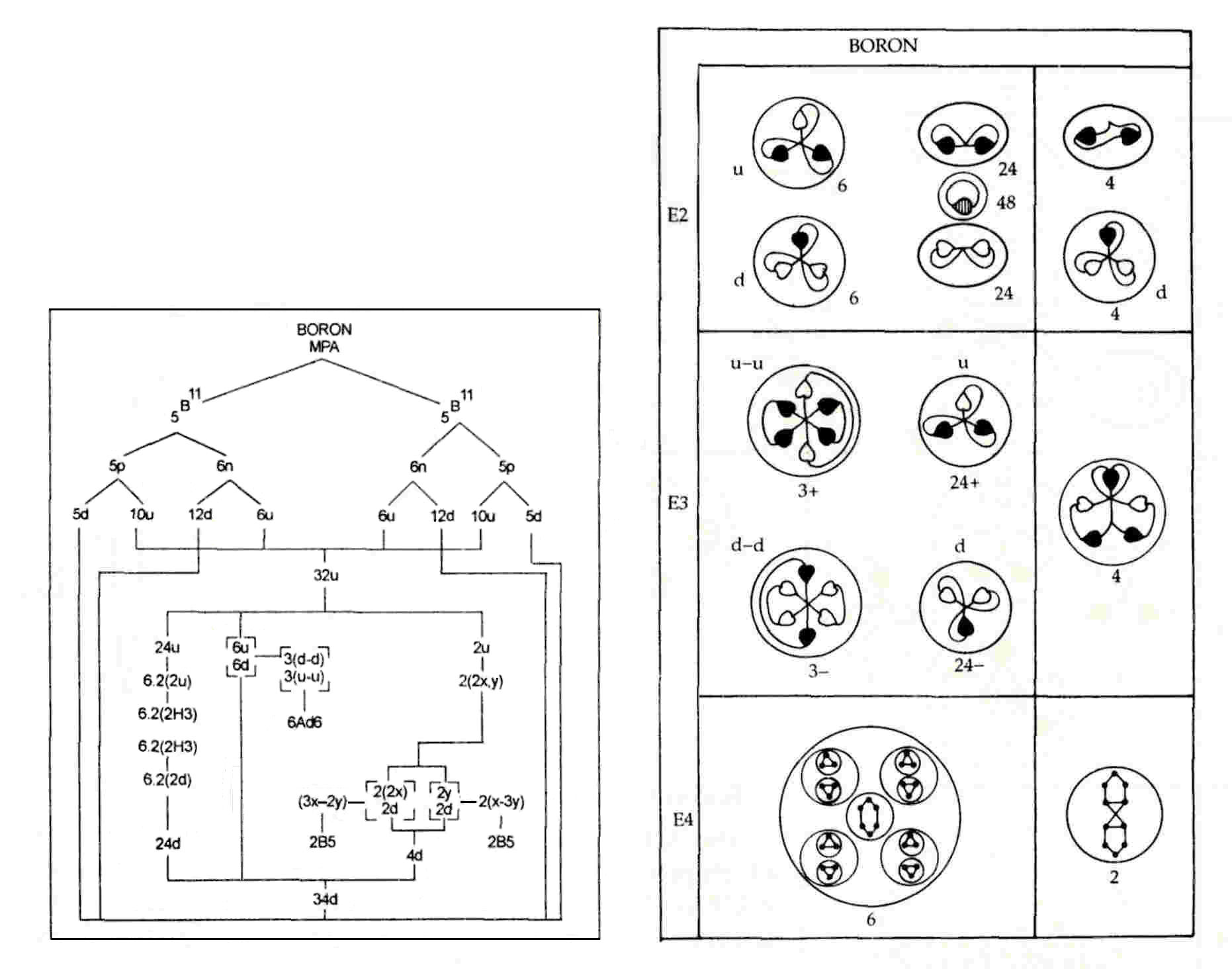 
disintegration diagram, which shows that twenty-four (+) triplets and twenty-four (−) triplets (d
quarks) are released from the funnels at the E3 stage of
disintegration. The diagram does not indicate whether the triplets in an ovoid are either both (+) or both (−) (as assumed above) or whether they consist of one of each type (the 1st edition of Occult Chemistry sheds no light on this matter). There is no stronger theoretical reason to make the former choice than that the pairs of d quarks supplied by the twelve neutrons in the two B11 nuclei remained together during the formation of the boron MPA.
The six Ad6 groups consist of three u-u diquarks and three d-d diquarks. The disintegration diagram confirms that there are three (+) Ad6 groups, which break up at the E2 stage into six (+) triplets (u quarks) and three (−) Ad6 groups, which split into six (−) triplets (d quarks).
The central globe is predicted to contain two B5 groups and two quartets of UPAs, not the observed four B5 groups. They consist of the eight X subquarks and ten Y subquarks making up the two u quarks and four d quarks remaining in the two nuclei after their thirty u quarks and thirty d quarks were released as pairs of H3 triplets or Ad6 groups. These subquarks regroup to form two B5 groups (3X-2Y) and two X-3Y bound states (Li4):
2u (= 2X-Y) + 4d (= X-2Y) = 8X + 10Y → 2(3X-2Y) + 2(X-3Y).
Alternatively, one B5 group could be the mirror state B5′ (2X-3Y), in which case the two quartets cannot be the same but, instead, consist of an X-3Y bound state (Li4) and a 2X-2Y bound state (Be4). The disintegration diagram confirms that one B5 group is a 3X-2Y bound state because it indicates that the group breaks up into a (−) triplet (d quark) and a (+) duad (X-X):
3X-2Y → d (= X-2Y) + X-X.
