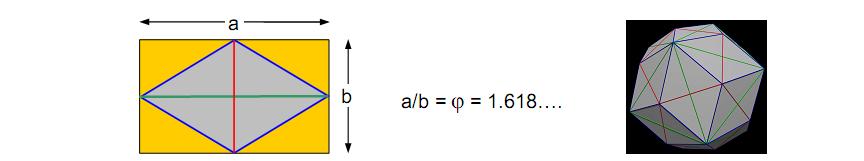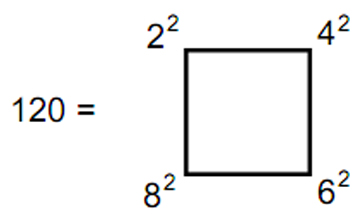ARTICLE 22

by

Stephen M. Phillips

Flat 4, Oakwood House, 117-119 West Hill Road. Bournemouth. Dorset BH2 5PH. England.

Website: http://www.smphillips.mysite.com

Abstract

1

(Numbers from this table that appear in the article will be written in boldface ).

2

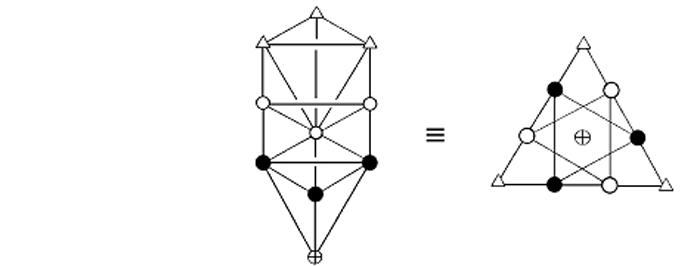
1. The Tetractys

At the heart of the philosophy of Pythagoras is the tetractys, the geometrical symbol of the Decad, or number 10, which his followers called “All Perfect” and “Kosmos”:

It is known to mathematicians as the fourth triangular number because it is the fourth member of the infinite set of integers 1, 3, 6, 10, etc, that can be expressed by triangular arrays of dots symbolising 1. However, the tetractys is far more than just a representation of the integers 1, 2, 3 & 4 — the numbers of dots in successive rows. These integers can be shown to express¹ the mathematical basis of all levels of reality, including space-time. This symbol of the perfect number 10 was revered by the ancient Pythagoreans because it is the key that unlocks information about reality —

 Figure 1. Equivalence of the tetractys and the Tree of Life.

physical and superphysical — embodied as numbers in objects that possess sacred geometry. Triangulating straight-edged objects and transforming their component triangles into tetractyses generates different classes of numbers defined according to the two basic types of dots in the tetractys. Its dots will be called ‘yods,’ named after the name of the tenth letter, י, of the Hebrew alphabet. The yods at the corners of the tetractys mark out the shape of a triangle — the simplest shape, whilst the six yods arranged at the corners of a hexagon and the yod at its centre are generated by the transformation of a triangle into a tetractys. The corner yods just define the triangle and are not generated by its transformation. The seven ‘hexagonal yods’ result or manifest when the triad of yods — the abstract symbol of form — transforms into a pattern that is now ten-fold. It is these hexagonal yods that represent new, formative degrees of freedom implicit in straight-edged objects possessing sacred geometry — new because they play no part in expressing their geometry per se, as this is the function of the yods at the corners of the tetractys.

The numbers revealed in geometrical objects by triangulating them and then turning their triangles into tetractyses are of three types:

1. number of yods belong to tetractyses;

2. numbers of corners of tetractyses. These numbers play a pre-formative, archetypal role;

3. numbers of hexagonal yods. These express formative degrees of freedom with structural or dynamical connotations.

The tetractys represents holistic systems, that is, systems that are whole manifestations of the Monadic Divine Life. Fig. 1 shows its relation to the ten Sephiroth of the Tree of Life. The corner yods symbolize the triple Godhead of Kether, Chokmah and Binah, and

3

the six yods at the corners of the hexagon denote the six Sephiroth of Construction above Malkuth, which is denoted by the yod at the centre of the hexagon. It is important to note that this equivalence means that the yods are not mere mathematical points. They express different aspects of God — spiritual potencies or energies, with the central yod symbolising the outer, physical form of a manifestation of the Divine Life, whether subatomic particle, the human body, the Solar System, etc.

As well as its outer form known to students of Kabbalah, the Tree of Life has been shown by the author to have an inner form made up of two identical sets of seven enfolded, regular polygons: triangle, square, pentagon, hexagon, octagon, decagon and dodecagon (Fig. 2). They share a single edge called the ‘root edge,’ so-called because they grow in succession out of it. The two sets of polygons are the mirror image of each other. The root edge extends from Daath to Tiphareth — or rather, their projection onto the plane containing the two sets of polygons, because the outer Tree of Life is three-dimensional and the central Pillar of Equilibrium is not a straight line and does not lie in the plane containing the Pillars of Mercy and Severity. The latter plane is that of the polygons, with Chokmah and Binah coinciding with the uppermost corners of the pair of hexagons, Netzach and Hod coinciding with their lowest corners and Chesed and Geburah coinciding with the outer corners of the two triangles (Fig. 3).

The polygonal form of the inner Tree of Life encodes how the outer form replicates itself as the generic template to map all the levels of consciousness that we, as beings ‘made in the image of God,’ have within us, waiting to be attained as we ascend the evolutionary path to the Godhead. As many previous articles have explained and as will be discussed later, this cosmic blueprint also encodes the three-dimensional form of the heterotic superstring and its gauge symmetry group E₈×E₈, where E₈ is the largest of the exceptional groups. These structural and dynamical encodings are now discussed.

2. Root structure of superstring gauge symmetry group E₈

Physicists Michael Green and Gary Schwarz made in 1984 the seminal discovery that superstrings had to possess a non-abelian gauge symmetry of order 496 in order for their interactions to be free of quantum anomalies. The only possible candidates are SO(32), E₈×E₈ and the trivial U(1)⁴⁹⁶. We shall focus here on the so-called heterotic superstring theory with E₈×E₈ as its gauge symmetry group. The roots of the E₈ algebra can be described in terms of eight orthonormal unit vectors {u_i}. Eight zero roots correspond to points at the centre of the root diagram and 240 non-zero roots all have length √2. They are given by

4

Their explicit forms as 8-tuples and their numbers are listed below:

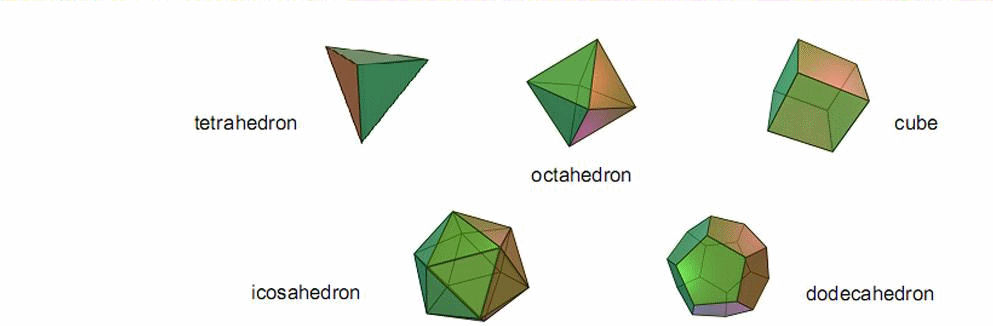
The gauge symmetry group of the E₈×E₈ heterotic superstring comprises (240+240=480) non-zero roots. Corresponding to each one is a generator of the Lie algebra of E₈×E₈, associated with which is a non-abelian gauge field whose quanta are messenger particles that transmit the forces between this type of superstring.

3. The Platonic solids

Thought by the ancient Greeks to be the shapes of the particles of the five elements, the Platonic solids (Fig. 4) are the five possible regular polyhedra. The tetrahedron, octahedron  and icosahedron have  triangular faces,  the cube has  square faces and the faces of the dodecahedron are

Figure 4. The five regular polyhedra, or Platonic solids.

pentagons. The triangular faces could be converted into tetractyses. However, this would be inconsistent with the division of the square into four tetractyses and the pentagon into five tetractyses. Hence, it must be divided into three tetractyses.

The triangular face contains 19 yods, nine on its three edges and ten inside its boundary (nine hexagonal) (Fig. 5). The square face has 25 yods, 12 on its edges

5

and 13 internal yods (12 hexagonal). The pentagon has 31 yods, of which 15 are on its boundary and 16 are internal (15 hexagonal).

The numbers of corners (C), edges (E) and faces (F) of a regular polyhedron are related by Euler’s equation:

C – E + F = 2.

Each edge has two hexagonal yods between its endpoints, which are corners. The number of yods in the faces of a regular polyhedron with each face a regular, n-sided polygon whose n sectors are tetractyses is given by

Y = C + 2E + nF = 2 + 3E + (n–1)F,

where n = 10 for the tetrahedron, octahedron and icosahedron, n = 13 for the square and n = 16 for the dodecahedron. The number of corners of tetractyses ≡ N = C + F = 2 + E. The number of hexagonal yods ≡ H = 2E + mF, where m = 9 for the tetrahedron, octahedron & icosahedron, m = 12 for the cube and m = 15 for the dodecahedron. The number of yods along the edges ≡ B = C + 2E. The number of yods at centres of faces = nF. The various yod populations of the Platonic solids are given below:

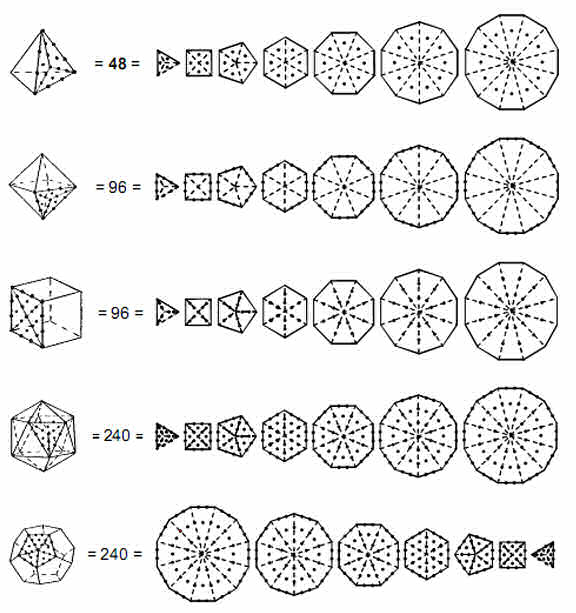
Tetrahedron

C = 4, E = 6, F = 4. Number of yods along edges = 16. Number of internal yods = 40. Number of yods on surface = 56. Number of hexagonal yods = 48. Number of corners of 12 tetractyses = 8.

Octahedron

C = 6, E = 12, F = 8. Number of yods along edges = 30. Number of internal yods = 72. Number of yods on surface = 110. Number of hexagonal yods = 96. Number of corners of 24 tetractyses = 14.

Cube

C = 8, E = 12, F = 6. Number of yods along edges = 32. Number of internal yods = 78. Number of yods on surface = 110. Number of hexagonal yods = 96. Number of corners of 24 tetractyses = 14.

Icosahedron

C = 12, E = 30, F = 20. Number of yods along edges = 72. Number of internal yods = 200. Number of yods on surface = 272. Number of hexagonal yods = 240. Number of yods at corners of the 60 tetractyses = 32.

Dodecahedron

C = 20, E = 30, F = 12. Number of yods along edges = 80. Number of yods inside faces = 192. Number of yods on surface of dodecahedron = 272. Number of hexagonal yods = 240.

The dodecahedron has the same number of yods (272) and the same number of hexagonal yods (240) as the icosahedron — the latter because they are dual to each other, so that they have the same combined number of corners and faces (32), that is, the same number of corners of tetractyses and therefore the same number of hexagonal yods. 272 is the number value of Cherubim, the Order of Angels assigned to Yesod.

The number of hexagonal yods in the icosahedron or dodecahedron is the same as the number of nonzero roots of E₈. This pair of Platonic solids therefore has the remarkable property that, when constructed from tetractyses, each of their hexagonal yods symbolise a non-zero root of the gauge symmetry group E₈×E₈ associated with the heterotic superstring. Indeed, the number of hexagonal yods in the 18 faces of the

6

tetrahedron, octahedron and cube is also 240.² This means that the four regular polyhedra, believed by the ancient Greeks to be the shape of the particles of the elements Earth, Water, Air and Fire, embody in their faces the number (480) of spin-1 gauge bosons transmitting the heterotic superstring force that are defined by the non-zero roots of E₈×E₈. As now explained, this is no accident, because the development of the Platonic solids, when constructed from tetractyses, follows precisely the pattern of transformation into tetractyses of the inner, polygonal form of the Tree of Life.

7

4. Inner Tree of Life counterpart of the Platonic solids

The seven separate regular polygons making up the inner Tree of Life have 48 corners. If their 48 sectors are converted into tetractyses, this may be considered to proceed in four stages (Fig. 6). The first stage is the appearance of the yod at the centre of each tetractys. There are 48 of these types of yods in the seven polygons. They correspond to the 48 hexagonal yods in the faces of a tetrahedron when its triangular faces are constructed from three tetractyses. Just as the simplest regular solid, the tetrahedron, embodies these 48 formative degrees of freedom, so 48 hexagonal yods appear at the first stage of transformation (being corners of tetractyses, the corners and centres of the polygons are prior to their transformation into tetractyses). Only the hexagonal yods are thus generated. Kabbalistically speaking, the number 48 is the number value of Kokab (“The Stellar Light”), the Mundane Chakra of Hod, to which the planet Mercury is traditionally assigned. The second stage is the appearance of two hexagonal yods on each of the 48 sides of the  polygons,  totalling  96 hexagonal  yods. They correspond to the 96 hexagonal yods in the faces of an 

octahedron when its triangular faces are divided into three tetractyses. The third stage is the appearance of two hexagonal yods on each of the 48 radial sides of the polygons, making a total of 96 hexagonal yods. They correspond to the 96 hexagonal yods in the faces of the third Platonic solid, the cube, when they are divided into four tetractyses. The fourth stage is the completion of the transformation of the polygons, which requires (48+96+96=240) hexagonal yods. These correspond to the 240 hexagonal yods in the faces of the icosahedron, the fourth Platonic solid. This 

completes the pattern of polygons, for the other set of polygons enfolded on the other side of the central Pillar of Equilibrium is identical, being the mirror image of the first. Their 240 hexagonal yods correspond to the 240 hexagonal yods in the faces of the dodecahedron when its pentagonal faces are divided into five tetractyses. Both sets of separate polygons contain (240+240=480) hexagonal yods. Each hexagonal yod symbolizes one of the non-zero roots of the superstring gauge

8

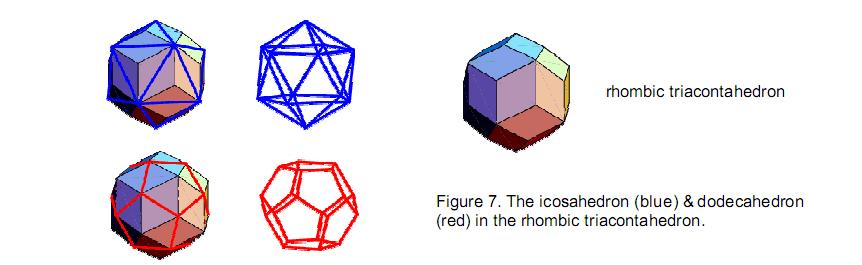
symmetry group E₈. The pair of identical sets of polygons, one the mirror image of the other, is the Tree of Life counterpart of the direct product of E₈ with itself. It indicates that the E₈×E₈ heterotic superstring is the type of superstring indicated by the Tree of Life blueprint. Each hexagonal yod denotes a spin-1 gauge boson that transmits the superstring force.

5. The rhombic triacontahedron

The rhombic triacontahedron, called “Kepler’s Solid” (Fig. 7), has 32 vertices, 60 edges and 30 golden rhombic faces, whose long diagonals of length a are edges of an icosahedron, whose short diagonals of length b are edges of a dodecahedron and where a/b = φ = 1.618…, where φ is the Golden Ratio (Fig. 8). The number of yods on edges of the rhombic triacontahedron = 2×60 + 32 = 152. As Fig. 8 shows, its 32 corners consist of the 12 corners of the icosahedron and the 20 corners of the dodecahedron. This leaves 120 hexagonal yods on edges, where

As we found earlier, the icosahedron has 272 yods in its faces, that is, 260 yods in addition to its 12 corners. Construction of the 20 triangular faces of the icosahedron from 60 tetractyses generates the yods in 26 tetractyses, illustrating how the mathematical archetype embodied in the Divine Name YAHWEH, which has number value 26, determines the fourth regular polyhedron. The dodecahedron also has 272 yods. The two regular polyhedra are dual to each other in that the corners of one are the centres of the faces of the other and vice versa. Combining them means that all

Figure 9. The 30 Golden Rhombic faces of the rhombic triacontahedron underlying the disdyakis triacontahedron are bases of 30 pyramids with 120 faces.

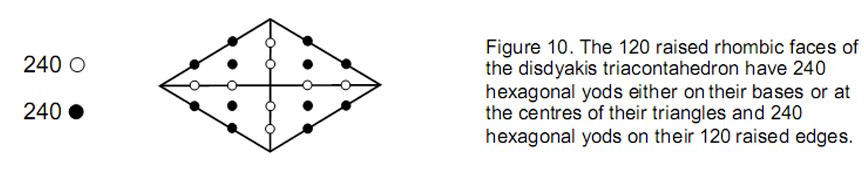
the corners and face centres of either one (32 in number) coincide with yods of the other. The number of yods in the faces of the combined pair of polyhedra = 272 + 272 – 32 = 512. Of these, 32 are corners of tetractyses, leaving 480 hexagonal yods. As expected, this is the number of hexagonal yods in the two separate polyhedra because, when they combine, only corners of tetractyses coincide, not any of their hexagonal yods.

The number of yods on the boundary of the icosahedron = C + 2E = 12 + 2×30 = 72. The number of yods on the sides of the dodecahedron = 20 + 2×30 = 80. The combined pair have (72+80=152) yods on their 60 edges, leaving (512–152=360) yods inside their boundaries, that is, the number of yods in 36 tetractyses. This shows how the Godname ELOHA assigned to the Sephirah Geburah with number value 36 determines the internal yod population of the two polyhedra. The Godname YAHWEH ELOHIM

9

assigned to Tiphareth with number value 76 determines the number of yods along their boundaries because 152 is the 76th even integer. As the rhombic triacontahedron also has 152 yods on its 60 edges, this Godname prescribes its shape.

6. The disdyakis triacontahedron

The 60 edges of the icosahedron and dodecahedron divide the 30 faces of the rhombic triacontahedron into (4×30=120) triangles. The disdyakis triacontahedron is the rhombic triacontahedron with these triangles raised (Fig. 9), that is, with each edge of the combined dodecagon and

icosahedron bent at their middle points. As a vertex lies above each face of the rhombic triacontahedron, whose 32 vertices are corners of triangles, the number of corners of the 120 triangles = 30 + 32 = 62. This is the 31st even integer, showing how the Godname EL with number value 31 assigned to the Sephirah Chesed prescribes the number of corners of the disdyakis triacontahedron. 62 is the number value of Tzadkiel (“Benevolence of God”), the Archangel assigned to Chesed.

As the rhombic triacontahedron has 60 edges and 30 faces, the number of edges of the 120 triangles = 60 + 4×30 = 180. Transformed into tetractyses, the number of yods on their edges = 62 + 180×2 = 422.  The number of yods at the centres of the 120 tetractyses = 120. The number of yods making up the faces of the disdyakis triacontahedron = 422 + 120 = 542.

The number of hexagonal yods in its faces = 542 – 62 = 480. 120 of these are at the centres of tetractyses. These correspond to the lowest Sephirah, Malkuth, leaving 360 hexagonal yods, that is, the yods in 36 tetractyses. The Godname ELOHA with number value 36 therefore determines the number of hexagonal yods corresponding to the six Sephiroth of Construction above Malkuth.

As found for the icosahedron and dodecahedron, the disdyakis triacontahedron has 480 hexagonal yods in its 120 faces. They comprise 240 hexagonal yods either on the edges of the rhombic triacontahedron or at the centres of the faces and 240 hexagonal yods on raised edges of the faces (Fig. 10), that is, two distinct sets of 240 hexagonal yods. They symbolize the 240 gauge bosons of E₈ and the 240 gauge bosons of the second group E₈ in the direct product E₈×E₈ for the heterotic superstring.

10

11

The disdyakis triacontahedron is the tenth member of the sequence of geometrical objects generated from a point:

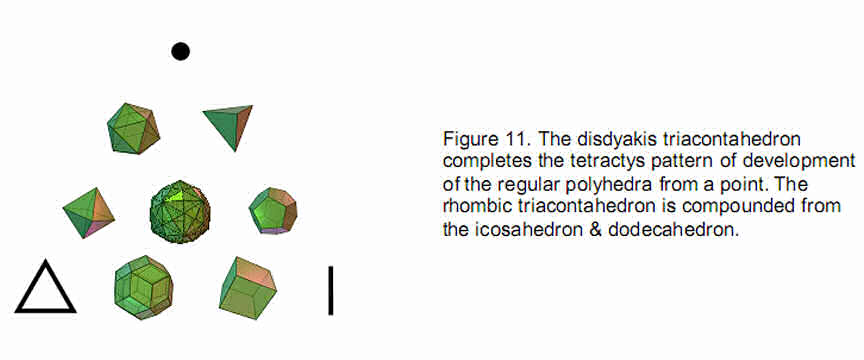
The first three members correspond to the corners of a tetractys because the point, line and triangle are the archetypal precursors of three-dimensional form. The disdyakis triacontahedron lies appropriately at the centre of the tetractys (Fig. 11) because the central yod of a tetractys symbolizes Malkuth, the last Sephirah, and this polyhedron embodies properties of the E₈×E₈ heterotic superstring — the basic unit of physical matter, which is what this Sephirah denotes.

That this sequence of geometrical objects truly constitutes an archetypal pattern is indicated by the fact that they have 150 vertices:

1 + 2 + 3 + 4 + 6 + 8 + 12 + 20 + 32 + 62 = 150.

This is the number of yods in 15 tetractyses, where 15 is the number value of YAH, the older version of the Godname assigned to Chokmah. A more spectacular reason will be given shortly.

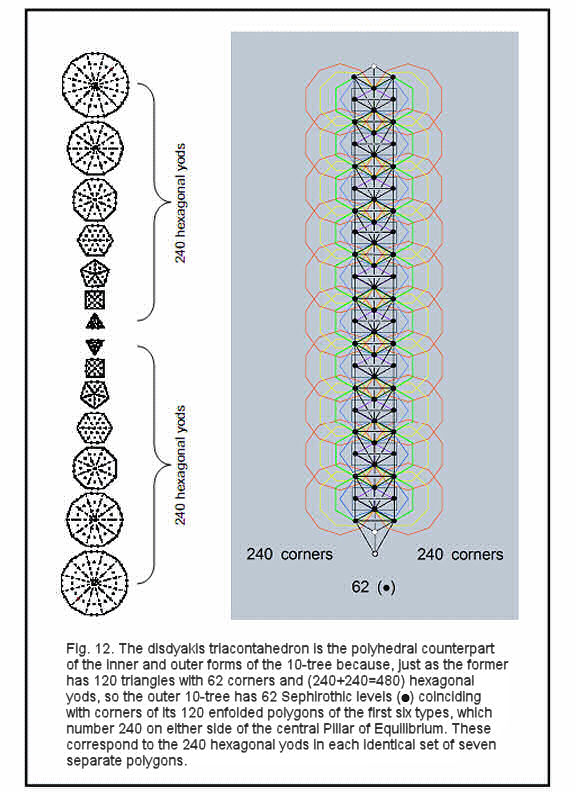
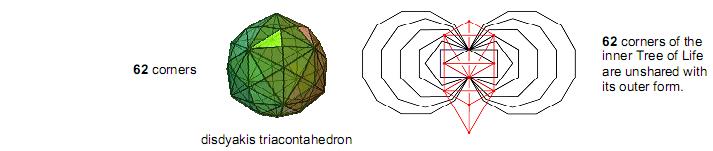
The disdyakis triacontahedron is the simplest polyhedron that embodies the group-theoretical parameters of the E₈×E₈ heterotic superstring. Its unique, archetypal significance lies in the fact that it is the polyhedral version of the so-called ‘10-tree,’ as now explained. The Tree of Life is a map of a holistic system in the minimal sense that each Sephirah can be represented in its own right by a Tree of Life. As there are ten Sephiroth, ten overlapping Trees of Life are an equivalent but more differentiated mapping of a holistic system. As shown in many previous articles, the Kabbalistic system of Divine Names, Archangelic Names, Orders of Angels and Mundane Chakras is a prescriptive set of non-arbitrary Hebrew words that, through gematria, have number values referring to this complete sequence of ten overlapping Trees of Life (the ‘10-tree’). They have 65 ‘Sephirothic levels,’ of which 62 coincide with corners of the first six polygons enfolded on each side of a tree when these points are projected onto the plane containing the 120 polygons (Fig. 12). This shows how the mathematical archetype embodied in the Archangel Tzadkiel with number value 62 prescribes the inner and outer form of the ten overlapping Trees of Life. The 62 corners of their triangles that are corners of polygons correspond to the 62 corners of the 120 triangular faces of the disdyakis triacontahedron. The first six enfolded polygons have 26 corners and both sets have 50 corners. 26 is the number value of YAHWEH, Godname of Chokmah, and 50 is the number value of ELOHIM, Godname of Binah, showing how these Hebrew Divine Names prescribe these sets of polygons. For each set enfolded in successive Trees of Life, there are two corners that are endpoints of their shared edge. This means that one endpoint can be associated with one set of polygons and the other endpoint can be associated with the other set, that is, 24 corners can be associated with either set. There are therefore 240 corners associated with each set of

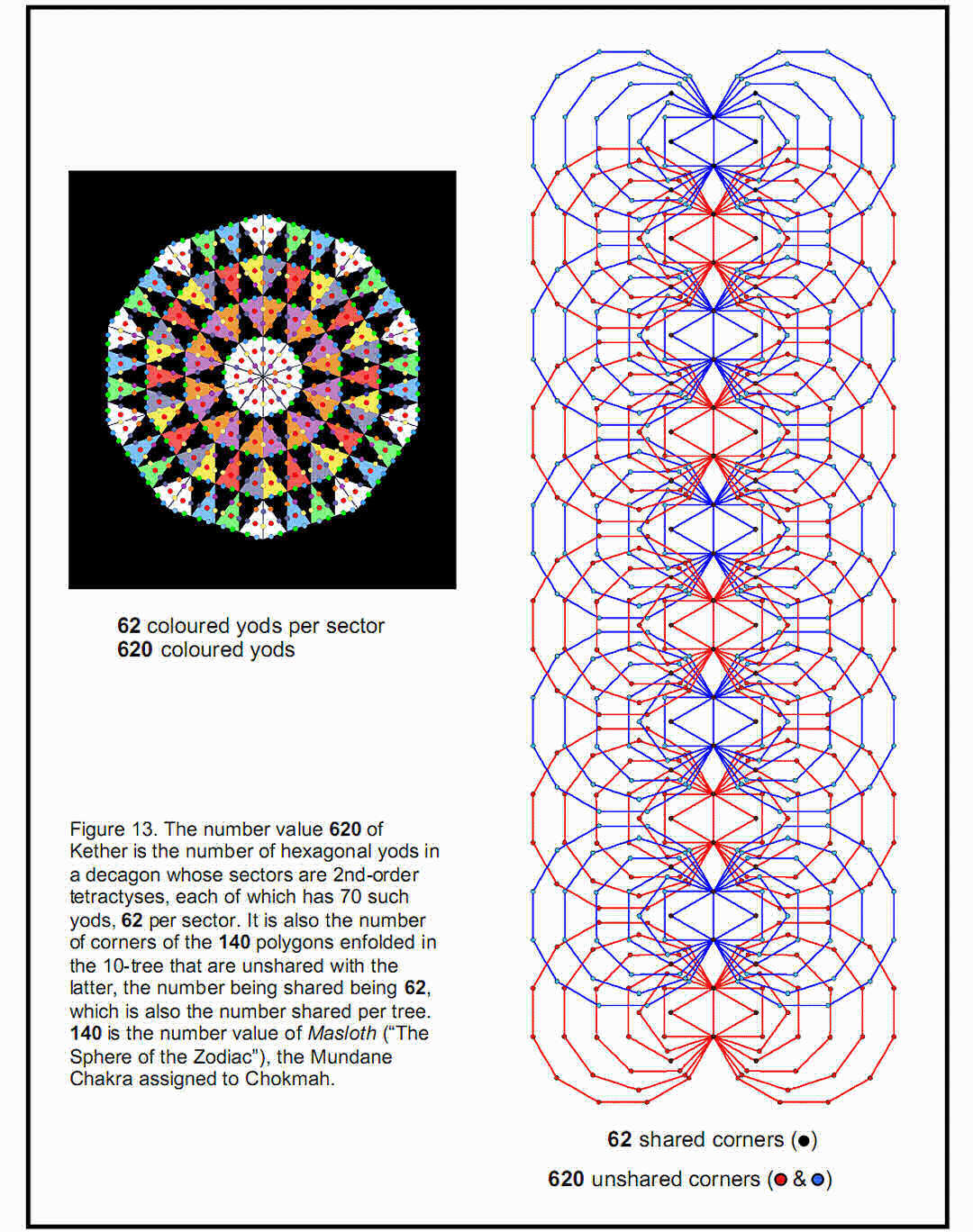
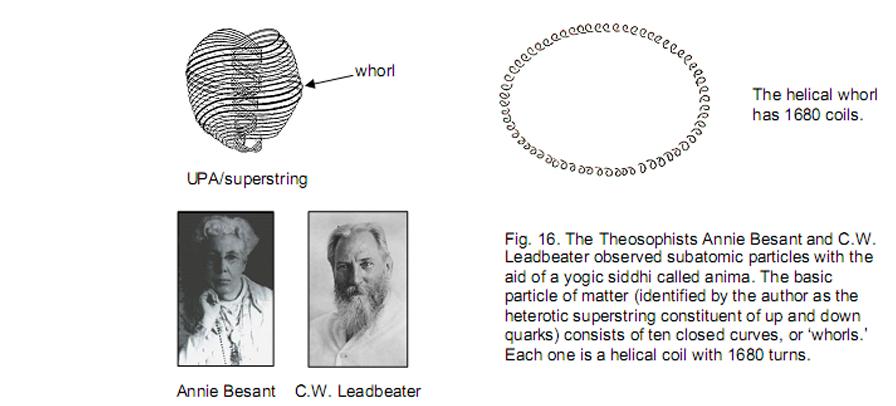
12

60 polygons enfolded in the ten Trees of Life. This 240:240 division of corners in ten sets of six enfolded polygons corresponds to the 240 hexagonal yods of each complete set of seven separate polygons (see Fig. 12).

The ten overlapping Trees of Life are a mapping of the 10-dimensional space-time of superstrings. Their inner polygonal (that is, 2-dimensional) form has (240+240)

13

independent geometrical degrees of freedom (corners unshared with Sephiroth of trees). They denote the (240+240) non-zero roots of the gauge symmetry group E₈×E₈ governing the unified interactions of heterotic superstrings. The 3-dimensional, polyhedral realisation of this encoding is the disdyakis triacontahedron with (240+240) hexagonal yods in its 120 triangular faces.

Further evidence of the underlying Tree of Life character of the disdyakis triacontahedron is the fact that, when the 61 yods of a decagon constructed from 10 tetractyses are each replaced by tetractyses, there appear 620 hexagonal yods, 62 per sector (Fig. 13).³ As the geometric symbol of the perfect Pythagorean Decad, the decagon contains 620 yods that are not corners of tetractyses. This is the number of Kether  (“Crown”), the first Sephirah. The remarkable Tree of Life counterpart of this is the fact that the 682 corners of the 140 polygons enfolded in ten Trees of Life

Figure 14. Eight corners of the two sets of seven enfolded polygons with 70 corners coincide with Sephiroth of the Tree of Life (although not a Sephirah, Daath must be included because it coincides with Yesod of the next higher, overlapping Tree of Life).  62  corners of the inner Tree of Life are unshared with its outer form. They correspond to the 62 corners of the disdyakis triacontahedron.

consist (as we saw earlier) of 62 that are shared with Sephiroth of each tree and 620 that are unshared. The former are indicated in Fig. 13 by black dots and the latter by red and blue dots. The 62 unshared corners associated with each of the ten trees correspond to the 62 hexagonal yods

Figure 15. The 120 shape-forming yods on the boundaries of the seven enfolded polygons symbolise the 120 faces of the disdyakis triacontahedron, which manifests the complete pattern of the Tree of Life.

per sector of the decagon. These independent yods and unshared corners represent intrinsic degrees of freedom of whatever possesses a Tree of Life pattern, as is indicated in Fig. 14, which shows that 62 of the 70 corners of the two sets of regular polygons making up the inner Tree of Life are unshared with its outer form and so constitute new geometrical degrees of freedom. Accordingly, the 62 corners of the faces of the disdyakis triacontahedron are the manifestation in

14

3-dimensional space of these degrees of freedom. It is the 3-dimensional (polyhedral) counterpart of the 2-dimensional (polygonal) inner form of the Tree of Life. This conclusion is supported by the fact that the shape of the inner form of the Tree of Life — the boundaries of the seven enfolded polygons — is delineated by the 120 yods that lie along their edges (Fig. 15). They symbolise the 120 triangular faces of the disdyakis triacontahedron, which, too, mark out its shape. As the seven enfolded polygons have 264 yods in 47 tetractyses,⁴ there are (264–120=144) yods inside their boundaries. They symbolise the 144 faces of another polyhedron, to be discussed in Article 23.

7. The seven polyhedra encode heterotic superstring structure

According to the properties of the five Platonic solids listed in Section 3, the total number of hexagonal yods in their 50 faces = 48 + 96 + 96 + 240 + 240 = 720. The rhombic triacontahedron was found  to have  480 hexagonal yods in its 30 faces — the same as the number of hexagonal yods in

the 120 faces of the disdyakis triacontahedron. The total number of hexagonal yods in the seven polyhedra = 720 + 480 + 480 = 1680. Amazingly, this is the number of circularly polarised oscillations in each whorl of the UPA described by Annie Besant and C.W. Leadbeater with micro-psi vision (Fig. 16)! The first three polyhedra — the tetrahedron, octahedron and cube — have 240 hexagonal yods in their 18 faces. This is repeated for the icosahedron and for the dodecahedron, then doubled for the rhombic triacontahedron and the disdyakis triacontahedron:

The seven polyhedra embody in their 200 faces the number of circularly polarised standing waves in each whorl of the heterotic superstring. Moreover, this number naturally divides into seven groups of 240 hexagonal yods — the type of yod

15

16

that denotes the Divine Qualities manifested by the seven Sephiroth of Construction. The same, seven-fold multiplication was found in Article 20 for the number of cube faces defining the eight corners of the cube at the centre of the 3×3×3 array of cubes symbolised by the 64 hexagrams of the I Ching table: 168 = 7×24, where ‘7’ denotes the number of cubes surrounding a corner of the central cube and 24 = 3×8, where ‘8’ denotes the number of corners of the central cube and ‘3’ is the number of mutually orthogonal cube faces whose intersection generates a corner. 168 is the number value of Cholem Yesodoth, Mundane Chakra of Malkuth (associated with the planet Earth).

As further evidence of the archetypal nature of the tetractys array of ten mathematical objects completed in the disdyakis triacontahedron, consider again the 10-tree. It is prescribed by the Divine Name ADONAI because it has 65 Sephirothic levels and 65 is the number value of this Godname:

We have seen that the 10-tree has 62 Sephirothic levels whose projection onto the plane containing the two sets of seven enfolded polygons coincides with some of their corners. It can be shown⁵ that, when the triangles making up these trees are divided into three triangles that are then converted into tetractyses, the number of yods below the top of the nth tree is

N(n) = 158n + 100.

The number of yods below the top of the tenth, overlapping Tree of Life is therefore

N(10) = 1680

(Fig. 17). Eight of these yods are in four triangles outside the tenth tree. The Godname ADONAI with number value 65 not only defines the lowest, ten overlapping Trees of Life. It also prescribes the superstring structural parameter 1680 as the number of yods below the 65th emanation marking the apex of the tenth tree. Any suggestion that this could be merely coincidental is refuted by the fact that the number value of Cholem Yesodoth, the Mundane Chakra of Malkuth, is 168. It is highly implausible that the appearance in the same context of two numbers associated with the most appropriate Sephirah — Malkuth — could be due to chance.

The number of triangles in the lowest n Trees of Life can be shown⁶ to be

T(n) = 12n + 7.

Hence, the lowest ten trees contain

T(10) = 127

triangles. 127 is the 31st prime number, where 31 is the number value of EL (“God”), אל, the Godname assigned to Chesed. This is another example of how the Hebrew Godnames prescribe the ten Trees of Life. Conversion of each triangle into three tetractyses generates (127×3=381) tetractyses. As, according to Fig. 17, the eight yods outside the tenth tree belong to four tetractyses, the 1680 yods belong to (381+4=385) triangles, where

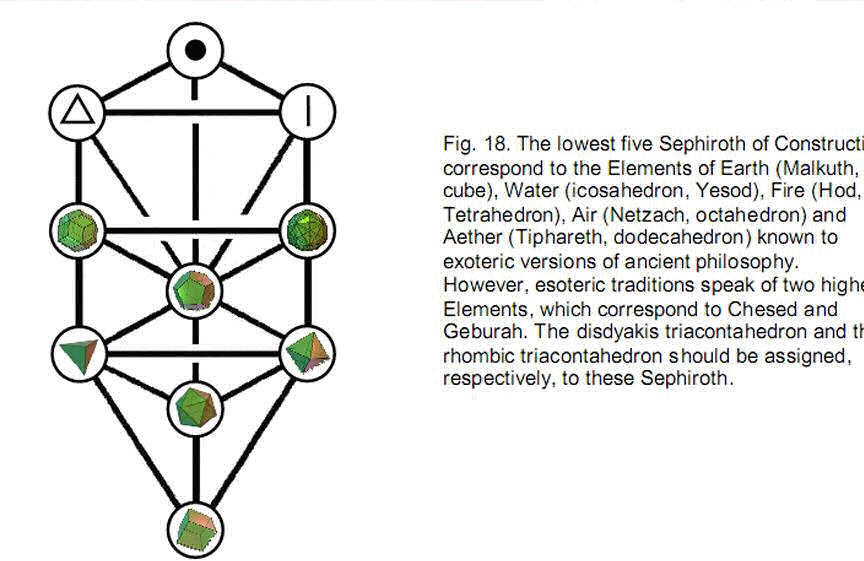
17

This demonstrates the beautiful, mathematical properties of the Tree of Life basis of the 1680 oscillations made in space by each whorl of the superstring.

There are 127 centres of triangles (each the corner of a tetractys) in the ten trees and 65 corners of these triangles. Inspection of Fig. 17 reveals that there is one corner of a tetractys on each side of the central pillar at the level of the apex of the tenth tree. There are (127+65+1+1=194) corners of tetractyses up to this point. 194 is the number value of Tzadekh (“Righteousness”), the Mundane Chakra of Chesed. We saw earlier that the number value 62 of Tzadkiel, the Archangel assigned to Chesed, is the number of the Sephirothic levels of the 10-tree that coincide with corners of the 70 enfolded polygons constituting the inner form of the 10-tree. Therefore, the Godname, Archangel and Mundane Chakra of Chesed have number values that characterize the 10-tree. Once again, this concurrence of numbers associated with the same Sephirah cannot be coincidental but, instead, is a remarkable manifestation of the connection between the geometrical properties of the Tree of Life and the Kabbalistic names of the spiritual hierarchy associated with each Sephirah.

Returning to the beautiful property of the seven polyhedra that they contain 1680 hexagonal yods symbolising the circularly polarised waves running around each whorl of the E₈×E₈ heterotic superstring, we can extrapolate the ancient association between the five Elements^* and the five

Platonic solids in order to include the  rhombic triacontahedron and the disdyakis triacontahedron. As first published by Plato in his Timaeus, a treatise on Pythagorean cosmology, the five Platonic solids, which were known to the early Pythagoreans, were thought to be the shapes of the particles of the five Elements. The cube was the particle of the Element Earth, the icosahedron was the shape of particles of Water, the tetrahedron was the shape of particles of Fire, the octahedron was the form of particles of Air and the dodecahedron with its approximate similarity to a sphere represented Aether. Kabbalists assign these Elements to the

^*The word ‘element’ is capitalized in order to distinguish its ancient meaning as states of matter from the modern, chemical meaning.

18

lowest five Sephiroth of Construction, starting with the cube, symbolising Earth, the dense physical state of matter, which corresponds to Malkuth. The Elements also represent the five types of awareness (sensory, feeling, thinking/conceptual, intuitive/imaginative and spiritual/holistic) found in Man. They correspond to the five ‘psychic functions’ formulated by Carl Gustav Jung, the great Swiss psychologist. Indian metaphysics also refers to the five tattvas of prithivitattva, apastattva, agnitattva, vayutattva and akashatattva, which are the atomic matters of the lowest five planes of consciousness. Some esoteric traditions add the anupadakatattva and the aditattva, the matter of the Theosophists’ anupadaka and adi planes of consciousness. The author has proved their doctrine of the seven planes of consciousness, which is encoded mathematically in the inner Tree of Life. Each plane or mode of being corresponds to a Sephirah of Construction. The purpose of evolution is to develop and integrate all these levels of being before passing over the Abyss of Daath as a jivamukti, or ‘liberated soul,’ to join the inner Divine Life of the Godhead within Binah, Chokmah and Kether.

Fig. 18 depicts the association between the seven polyhedra and the seven Sephiroth of Construction, keeping consistent with both the Kabbalistic association of Elements with these Sephirah and their Platonic association with the regular polyhedra. The dodecahedron is associated with Tiphareth because the Element Aether or Akasha is the fifth most subtle Element and Tiphareth is the fifth Sephirah of Construction, counting from Malkuth. The rhombic triacontahedron is associated with Geburah and the disdyakis triacontahedron with Chesed, the first Sephirah of Construction. The reason for this assignment is intuitively obvious. Just as the Sephiroth of Construction emerge from the first one, Chesed, that is, as the mathematical archetypes become less general and more specific, so all the Platonic solids and the rhombic triacontahedron are present in the disdyakis triacontahedron, whose greatest geometrical generality requires it to correspond to the first Sephirah of Construction. The point corresponds to Kether, the line to Chokmah and the triangle to Binah.

The following associations can be made if, instead of ordering the polyhedra according to their ancient associations, the reasons for which were naïve, we list them simply according to their number of vertices: 

1. tetrahedron Chesed
2. octahedron Geburah
3. cube Tiphareth
4. icosahedron Netzach
5. dodecahedron Hod
6. rhombic triacontahedron Yesod
7. disdyakis triacontahedron Malkuth

If they were listed according to their number of faces, this would place the icosahedron after the dodecahedron. In a strict mathematical sense, neither is more general because one is the dual of the other. Their association, however, with the Elements makes their ordering matter in a metaphysical sense. We saw in Article 3 that the dodecahedron embodies both the number (91) of Trees of Life in CTOL and the number (550) of Sephirothic levels that they possess.⁷ This polyhedron must be regarded as the fifth Platonic solid, not the fourth, because it embodies properties of CTOL, the spiritual cosmos that the ancient Greeks identified with the celestial sphere and with which the fifth Element Aether came to be associated. Their association of the tetrahedron, octahedron, cube & icosahedron with the four physical Elements was correct even though the reasons Plato gave for this have no fundamental significance. When we ignore the bogus historical associations between each Platonic solid and its Element,

19

there emerges the following correspondences between the seven Sephiroth, the seven tattvas and the seven polyhedra:

This preserves the crucial group association of the five exoteric elements with the five Platonic solids and the lowest five Sephiroth of Construction, though not some of their individual associations (but, then, the latter, do not matter because they have no theoretical basis). The number of vertices decreases monotonically until we arrive at the tetrahedron. If the polyhedra were ordered according to increasing numbers of vertices, it would destroy the correspondence between Sephiroth of Construction and the Elements with which they were historically associated, e.g., the cube would be associated with Tiphareth (Aether), which is clearly wrong. This ordering is therefore incorrect. Similarly, if they were ordered according to the number of faces:

the dodecahedron with 12 faces would be fourth in the list whether the numbers increased or decreased, thereby destroying the association between Elements/tattvas and Platonic solids. This must also be incorrect. We are therefore left with only one possible set of correspondences — that shown above.

References

1. Phillips, Stephen M. “The Mathematical Connection between Religion and Science” (Antony Rowe, Publishing, England, 2009);

2. Phillips, Stephen M. Article 3: “The Sacred Geometry of the Platonic Solids,” (WEB, PDF).

3. Proof: the tetractys formed by replacing yods of a tetractys with tetractyses has 85 yods.15 of these are corners of the 10 tetractyses and 70 are hexagonal yods. Eight hexagonal yods lie along each side of such a tetractys. Turning the sectors of a regular polygon into tetractyses and then replacing their yods by tetractyses creates (70–8=62) hexagonal yods per sector. A decagon with 10 sides therefore contains (62×10=620) hexagonal yods.

4. Proof: the triangle has 19 yods, the square has 25 yods (21 outside the shared root edge), the pentagon has 31 yods (27 outside the root edge), the hexagon has 37 yods (33 outside the root edge, of which 6 are shared with the triangle, leaving 27 yods), the octagon has49yods (45 outside the root edge), the decagon has 61 yods (57 outside the root edge, of which one — the central yod — is a corner of the pentagon, leaving 56 yods) and the dodecagon has 73yods (69 outside the root edge). Number of yods in the seven enfolded polygons = 19 + 21 + 27 + 27 + 45 + 56 + 69 = 264.

5. Proof: there are 5 corners of triangles up to Tiphareth of the lowest tree. Then there are 6 corners for every higher tree. The number of corners up to the top of the nth tree is therefore 6n + 5. There are 9

20

sides of 7 triangles up to Tiphareth of the lowest tree. The lowest tree contains 19 triangles with 25 sides, that is, (19–5=12) triangles with (25–9=16) sides outside the area enclosed by the lowest five Sephiroth. Then there are 12 triangles with 16 sides for every higher tree. The number of triangles up to the top of the nth tree is 12n + 7. They have (16n+9) sides. Converted into three tetractyses, a triangle contains 19 yods, of which 10 are inside it. Noting that each side of a triangle has two yods between its two ends, the number of yods in the lowest n trees = the number of corners + 2×number of sides + 10×number of triangles = (6n+5) + 2(16n+9) + 10(12n+7) = 158n + 93. Below the top of the nth tree and outside it are 8 yods (4 on each side of the central pillar; see Fig. 16). The number of yods below the top of the nth tree = 158n + 93 – 1 + 8 = 158n + 100.

  6.   Ibid.

    7.  Ref. 2, p. 11.

21