|
ARTICLE 47 (Part 1)
|
||
|
|
||
|
|
by Stephen M. Phillips Flat 4, Oakwood House, 117-119 West Hill Road. Bournemouth. Dorset BH2 5PH. England. Website: http://smphillips.mysite.com |
|
|
|
||
Page Index
|
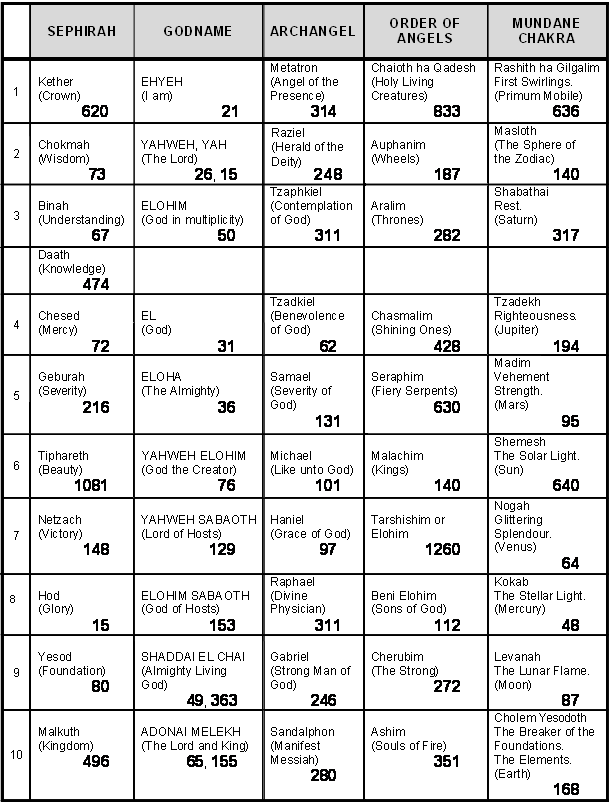
Part 1 Page Table of number values of the Sephiroth in the four Worlds .
. . . . . . . . . . . . . . . . . . . .3 |
Page Table of number values of the Sephiroth in the four Worlds .
. . . . . . . . . . . . . . . . .1 |
 |
|
As well as the Tree of Life known to Kabbalists for hundreds of years, which may be called the ‘outer form’ of this blueprint for holistic systems embodying the divine paradigm, there is an ‘inner form’ of this geometrical object. It consists of two sets of seven regular polygons:
triangle, square, pentagon, hexagon, octagon, decagon & dodecagon.
One set is the mirror image of the other. They are joined at the ‘root edge.’ The plane in which they lie passes through the vertical Pillars of Mercy and Severity but not through the central Pillar of Equilibrium, because the outer form of the Tree of Life is really three-dimensional, not two-dimensional, as usually depicted in books on Kabbalah. This means that the Sephiroth Chokmah, Chesed, Netzach, Binah, Geburah & Hod are located at corners of the triangles and hexagons but that Tiphareth and Daath do not coincide with the endpoints of the root edge —only their projections onto the plane of the polygons do.
|
|
The number 137 is embodied in the blueprint of the inner Tree of Life. Its (7+7) enfolded polygons have 94 sectors. When each sector is divided into three tetractyses, 1370 yods are generated, i.e., the number of yods in 137 tetractyses. This proves beyond reasonable doubt that the number 137 is a basic structural parameter of the Tree of Life, in keeping with its central status in physics as a number which determines one of the fundamental constants of nature — the fine-structure constant, whose magnitude sets the scale of the energies of electrons in atoms.
|
|
Ten overlapping Trees of Life map the 10-dimensional space-time of superstrings. With their triangles turned into tetractyses, there are 248 (red & violet) yods up to Chesed of the fifth tree — its first Sephirah of Construction. There are a further 248 (blue) yods up to, but not including, Chesed of the tenth tree. Each yod denotes a particle, a gauge field of E8 or E8'. The Godname EL of Chesed with number value 31 prescribes the dimension 248 of E8 because there are 31 emanations up to Chesed of the fifth tree.
|
|
According to E8×E8' superstring theory (one of the five types of superstrings), the unified force between such superstrings is mediated by virtual exchange of the 248 gauge bosons of E8 (ordinary matter) and the 248 gauge bosons of E8' (shadow matter). An ancient symbol of the four elements of Earth, Air, Fire & Water, the square encodes this information. When its sectors are turned into 2nd-order tetractyses, the next higher differentiation of the Pythagorean tetractys:
they contain 248 hexagonal yods (the yods at the corners are omitted so as make clear which yods are being counted). Each one symbolises a Sephirah of Construction as well as a possible quantum state of the spin-1 particle that transmits the force between this type of superstring.
|
The E8 root system consists of 240 vectors in an eight- dimensional space. Those vectors are the vertices (corners) of an eight-dimensional object called the Gosset polytope 421. In the 1960s, Peter McMullen drew (by hand) a 2-dimensional representation of 421. In 2007, a four-year collaboration between mathematicians from Europe and the USA announced the results of their calculations of the mathematical structure of E8, using a supercomputer. The image shown here was computer-generated by John Stembridge, based on McMullen's drawing. (Credit: Image courtesy of American Institute of Mathematics)
|
The Gosset polytope 421 |
An octagon whose sectors are transformed into 2nd-order tetractyses has 496 hexagonal yods. Each yod symbolizes a particle involved in the transmission of the superstring force. The number of tetractyses is 80. This is the number value of Yesod, the Sephirah immediately above Malkuth in the Tree of Life. This archetypal pattern is prescribed by the Godnames. For example, it is prescribed by the Godname YAH with number value 15 because each sector of the octagon has 10 tetractyses with 15 corners. There are 576 yods surrounding the centre of the octagon, where 576 = 242 = 12×22×32×42. 33 yods are corners of 1st-order tetractyses, where 33 = 1! + 2! + 3! + 4!. These are examples of how the integers 1, 2, 3 & 4 symbolized by the four rows of the Pythagorean tetractys express the properties of archetypal patterns and holistic systems possessing sacred geometry.
|
|
|
|
Outside the root edge of the last four polygons of the inner Tree of Life whose sectors are divided into three tetractyses are 496 yods other than their corners and centres:
This property might be dismissed as a coincidence were it not for the fact that the hexagon & dodecagon have 248 yods and the octagon & decagon have 248 yods. In other words, the yod population 496 splits into two identical numbers (248), in conformity with the prediction by E8×E8' heterotic superstring theory. Even supposing that it were mere coincidence that the last four polygons have 496 such yods, it is highly improbable that subsets of them also by chance have yod populations that add up to 248. It is therefore reasonable to discount chance. This property demonstrates how the universal blueprint of the inner Tree of Life embodies the dynamics of the E8×E8' heterotic superstring.
|
|
The basic unit of matter was depicted in 1878 by an American pioneer of colour therapy, Dr. Edwin D. Babbitt, in his book "The Principles of Light and Color" and in 1952 in the 3rd edition of the book Occult Chemistry written by the Theosophists, Annie Besant and Charles W. Leadbeater, who called it the ‘ultimate physical atom,’ or UPA. They noticed two types of UPA, one the mirror image of the other. The UPA consists of ten closed curves, each of which revolves five times around the axis of spin of the particle. Each curve is a helix with 1680 circular turns. Three curves (‘major whorls’) are thicker and brighter than the other seven (‘minor whorls’). They are the microscopic manifestation of the ten Sephiroth of the Tree of Life. The ten whorls have 16800 helical turns (3360 turns per revolution).
As 132 – 1 = 168 and a parallelogram constructed from two 2nd-order tetractyses has 13 yods along each side, a 10-pointed array of 10 parallelograms has 1680 yods surrounding its centre. They comprise 90 yods in each inner 2nd-order tetractys and 78 yods in the remainder of a parallelogram. This reproduces the gematria number values of the two Hebrew words in Cholem Yesodoth, the Kabbalistic name of the Mundane Chakra of Malkuth:
|
|
|
|
The semi-regular polyhedra are divided into two groups of 13 (15, if enantiomorphs are included). They are called the Archimedean solids and the Catalan solids (their duals, in which vertices & faces are interchanged). The Catalan solid with the most faces is the disdyakis triacontahedron. It has 62 vertices, 180 edges & 120 triangular faces. Each edge can be thought of as the base of an interior triangle with a corner at the centre of the polyhedron. If these triangles are divided into their sectors, it can be calculated that 1680 vertices, edges & triangles surround an axis passing through any two diametrically opposite vertices. This is the number of turns made in each helical whorl of the E8×E8' heterotic superstring as it revolves five time around its axis of spin. It is an indication that the disdyakis triacontahedron is the polyhedral version of the Tree of Life, which encodes the same structural parameter of superstrings.
|
|
The Decad specifies the dodecagon as the tenth regular polygon. Construction of each of its sectors from three tetractyses requires 168 more yods. 84 yods lie on edges of tetractyses inside sectors and 84 yods either lie on edges of sectors or are centres of tetractyses. This 84:84 division of the superstring structural parameter 168 is characteristic of holistic systems embodying the universal patterns of sacred geometry. A dodecagon has 156 hexagonal yods. 155 hexagonal yods are associated with each of the two joined dodecagons. 155 is the number value of ADONAI MELEKH, the Godname of Malkuth, and 168 is the number value of its Mundane Chakra. This demonstrates how the Godname of the Sephirah signifying the material universe determines the form of the basic units of matter.
|
|
|
|
The fact that 168 yods surround the centre of a square whose sectors are each divided into triangles which are then constructed from tetractyses is an illustration of the Tetrad Principle, whereby the fourth member of a class of mathematical objects, or the fourth stage in its construction from tetractyses, always represents a parameter of the Tree of Life. In this case, the square is the fourth stage in the sequence:
point—line—triangle—square—pentagon, etc
and the superstring structural parameter 168 is the number of yods needed for its fourth stage of construction from tetractyses.