|
Article 40

Part 4
by
Stephen M. Phillips
Flat 3, 32 Surrey Road South.
Bournemouth. Dorset BH4 9BP. England.
Website:
http://www.smphillips.mysite.com
1
|
Figure 1
The graph shows the positions of the 62 vertices of the disdyakis
triacontahedron projected onto the XY plane with the Z axis running through two
diametrically opposite C vertices. 60 vertices are corners of polygons in 15 layers.
Solid lines of the same colour connect vertices at the same height above the XY plane.
Dashed lines of the same colour connect vertices at the same depth below the XY plane.
Vertices at the same height form either triangles or 6-sided polygons, with six A
vertices in the XY plane located at the corners of a hexagon. Suppose that the 60
sectors of these polygons are each constructed from three triangles. The latter share
one corner at the centre of each sector. 15 of the corners of the 180 new triangles are
the centres of the polygons, so that they have (15+60=75) corners inside the polyhedron
and 60 corners that are polyhedral vertices. Including the C vertices at its apex and
nadir, there are (75+60+2=137) vertices. This number is one of the most important
numbers in physics because it defines approximately as its reciprocal the
fine-structure constant e2/ħ c that measures the strength of the coupling of
electrically charged particles to the electromagnetic field. Appropriately, the number
determining the electron structure of atoms is embodied in the sheets of vertices of
the disdyakis triacontahedron as the number of vertices needed to construct its faces
and interior from triangles.
If the triangles are now turned into tetractyses, the transformation
requires 840 new yods. This is the number of turns in each helical whorl of the
heterotic superstring as it spirals 2½ times around its spin axis, making half a
complete circuit. The disdyakis triacontahedron embodies this structural parameter of
the heterotic superstring.
2
Figure 2
Suppose that the seven polygons above the XY plane formed by
vertices of the disdyakis triacontahedron are divided into their sectors and the latter
then constructed from three tetractyses. There are 378 yods other than polyhedral
vertices surrounding the centres of the seven polygons. This is the number of yods
needed to turn the 42 triangles of the 3-dimensional Sri Yantra into tetractyses. Their
42 black centres correspond to the 42 black yods surrounding the centre of the
uppermost triangle that are not vertices of the polyhedron. The 84 red yods at corners
of tetractyses correspond to the 84 similar red yods in the next two triangles. The 84
green, hexagonal yods on the 42 edges of the 14 tetractyses in the fourth layer of the
Sri Yantra correspond to the 84 green yods in the other two triangles. The 168 yellow,
hexagonal yods on the 84 edges of the 28 triangles in the first three layers correspond
to the 168 yellow yods in the pair of six-sided polygons.
In either case, the 378 yods symbolize the 378 rising and falling
intervals other than the octave between the notes of the seven musical scales.
4
There
are 378 yods other than polyhedral vertices surrounding the centres
of the seven polygons
above
the equatorial plane of the disdyakis triacontahedron. This is the
number of yods in the
42
triangles of the 3-d Sri Yantra. They symbolize the 378 rising and
falling intervals below the
octave
of the notes in the seven musical scales.
5
|
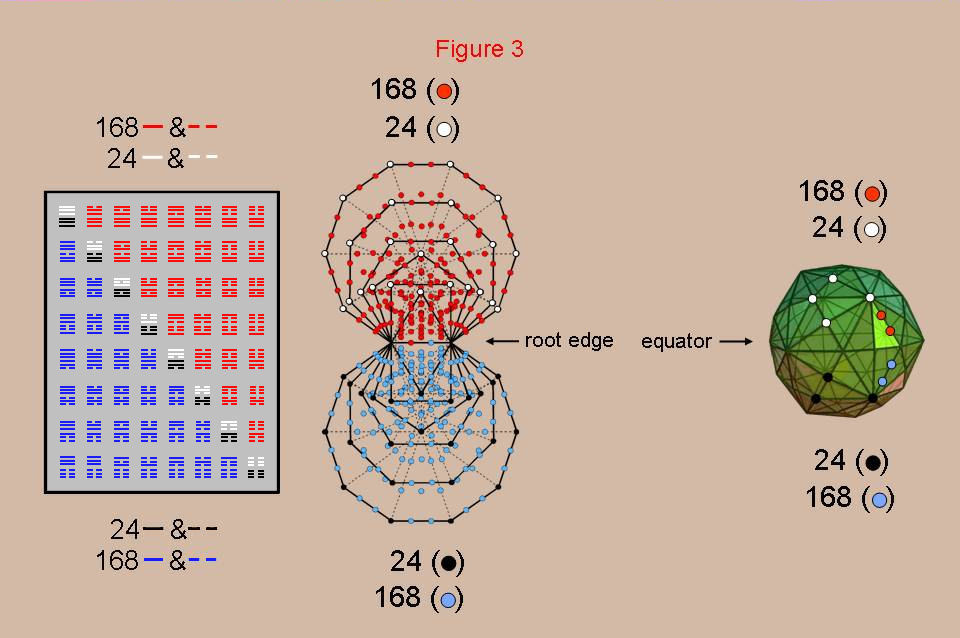
Figure 3
The I Ching table, the inner Tree of Life and the disdyakis
triacontahedron are equivalent representations of holistic systems, as now shown. Of
the 62 vertices of the disdyakis triacontahedron, 12 vertices (four A, four B &
four C vertices) are in the XY plane when the Z axis passes through two diametrically
opposite A vertices. Hence, there are 50 vertices above and below this plane, i.e., 24
vertices lie between the XY plane and the uppermost or lowest A vertex. One set
corresponds to the 24 lines/broken lines in the upper trigrams of the eight diagonal
hexagrams, the other set correspond to the 24 lines/broken lines in the lower trigrams.
12 of the 180 edges of the polyhedron are in the XY plane, leaving 84 edges above this
plane and 84 edges below it. Two hexagonal yods lie on each edge. (2×84=168) red
hexagonal yods lie on edges above the plane and 168 blue hexagonal yods lie on edges
below it. Each set of 168 hexagonal yods corresponds to the 168 yods other than corners
associated with each set of six enfolded polygons and to the 168 lines/broken lines in
the 28 hexagrams above or below the diagonal of the I Ching table.
6
|
Isomorphism between the I Ching, the
inner
Tree of Life & the disdyakis
triacontahedron.
7
|
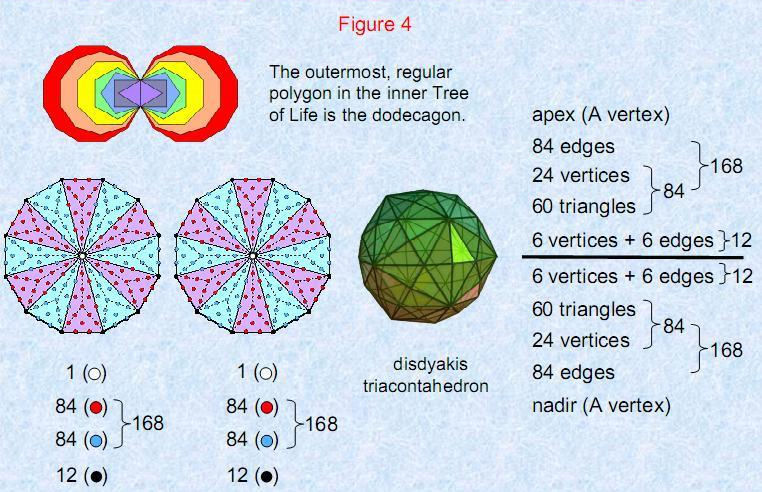
Figure 4
The outermost polygon in the inner Tree of Life is the dodecagon.
168 extra yods are needed (84 in six sectors) to construct each of its 12 sectors from
three tetractyses. The disdyakis triacontahedron has 84 edges and 24 vertices and 60
triangles above the XY plane, that is, another 84 geometrical elements. Similarly below
this plane, which contains 12 vertices and 12 edges. Hence, the 84:84 division of yods
in the dodecagon has its counterpart in the 84:84 division of geometrical elements
above or below the equator of the disdyakis triacontahedron.
The centres of the two dodecagons correspond to the A vertices at
the top and bottom of the polyhedron. The 12 corners of each dodecagon correspond to
the 12 vertices & edges in the XY plane and their mirror images. The two sets of 84
new yods in each dodecagon correspond to the 84 edges and 84
vertices/triangles above or below the XY plane. Each yod in the pair of dodecagons
symbolizes a geometrical element composing the disdyakis triacontahedron. The yods
denote the ‘bits of information’ needed to construct the polyhedral form of the inner
Tree of Life.
8
Isomorphism
between the disdyakis triacontahedron and
the pair of dodecagons of the inner Tree of
Life.
9
|
Figure 5
Each of the 120 triangular faces of the disdyakis triacontahedron
has an A, B & C vertex. The polyhedron has 60 AB edges, 60 BC edges and 60 AC
edges. The 12-sided polygon in the equator has four AB edges, four BC edges and four AC
edges. This leaves 56 sets of three different types of edges above and below the XY
plane, when the Z axis passes though two diametrically opposite A vertices, that is,
168 edges in 56 sets of three shape its 3-dimensional form.
Compare that property of the disdyakis triacontahedron with the 56
triangles with 168 vertices needed for the {3,7} tiling in the hyperbolic plane of the
168 symmetries of the Klein quartic belonging to PSL(2,7). Also notice that there are
24 vertices, 84 edges and 60 triangles, that is, 168 geometrical elements, between the
XY plane and the apex of the polyhedron and 168 elements between this central plane and
its nadir. These (168+168=336) elements correspond to the 336 triangles needed in the
{7,3) tiling of the 168 automorphisms and 168 anti-automorphisms of the Klein quartic.
The two sets of 168 symmetries correspond to the 168 geometrical elements either above
or below the equator of the disdyakis triacontahedron between opposite vertices. The
PSL(2,7) and SL(2,7) groups are embodied in the geometry of this polyhedron. PSL(2,7)
is isomorphic to SL(3,2), the symmetry group of order 168 of the Fano plane that
represents the algebra of the octonions, which form a natural representation of the Lie
algebra of E8, the unified superstring gauge symmetry group. This indicates
that a connection exists between the geometry of the disdyakis triacontahedron and
superstring dynamics.
10
The disdyakis
triacontahedron is the polyhedral embodiment of
SL(2,7).
11
|
Figure 6
The I Ching table, the Sri Yantra, the inner Tree of Life, the Klein
configuration and the disdyakis triacontahedron exhibit a universal 168:168 pattern in
their geometries. It is highly implausible that this is a coincidence. Instead, it
strongly indicates the relevance to theoretical physics (in particular, to string/brane
theory) of the group SL(2,7) of order 336, which is the double-cover group of PSL(2,7)
of order 168. It is further suggested by the fact that the basic constituent of matter
described by Annie Besant and C.W. Leadbeater over a century ago consists of ten closed
curves, each of which is a circularly polarized standing wave that makes 168
oscillations in half a revolution around the spin axis of the particle. Its inner and
outer halves with 168 helical turns per half-revolution are the manifestation of the
mirror/inversion symmetry of these isomorphic objects of sacred geometry or – in the
case of the I Ching table – the Yin/Yang balance of the 168 unbroken lines and the 168
broken lines of its 64 hexagrams.
12
Figure 7
Each Sephirah has a corresponding Godname, Archangel, Angelic Order
& Mundane Chakra. The Mundane Chakra of Malkuth, the last Sephirah of the Tree of
Life signifying the physical universe, is called in Hebrew “Cholem Yesodoth.” It means
“breaker of the foundations.” Its gematria number value is 168. The number value of
Cholem is 78 and the number value of Yesodoth is 90.
14
Cholem Yesodoth, the Hebrew name of
the Mundane Chakra of Malkuth
(physical universe) has the gematria
number value of 168.
15
|
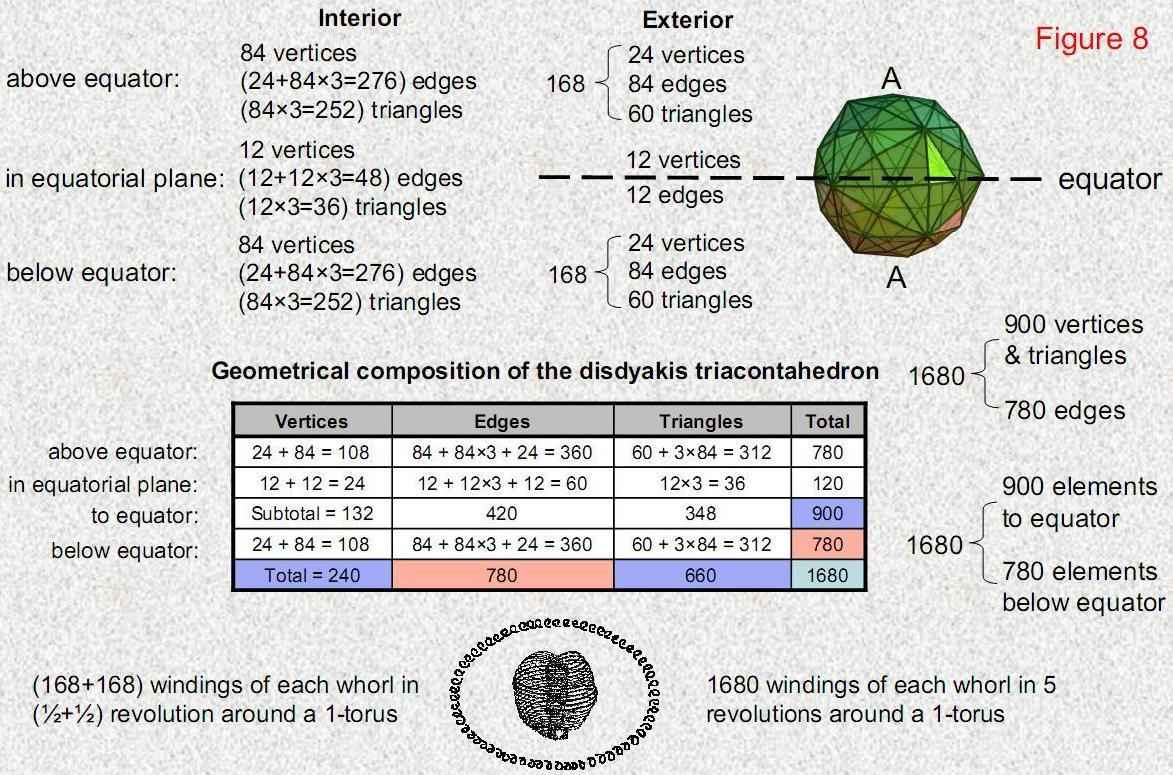
Figure 8
Consider the disdyakis triacontahedron constructed internally as
well as externally from triangles. Each of its 180 edges is then the base of a triangle
one of whose vertices is the centre of the polyhedron. Then suppose that these internal
triangles are each divided into three triangles. This generates 168 vertices above and
below the equator of the polyhedron with ‘A’ vertices (peaks of its 30 rhombic
pyramids) at its apex and nadir. Surrounding the vertical axis joining these two
vertices, there are 168 vertices & triangles above the equator, 168 vertices &
triangles below the equator and 168 edges above and below it that are in its 120 faces.
Surrounding the axis of the disdyakis triacontahedron are 660 triangles with 240
vertices, i.e., 900 geometrical elements, and 780 edges, making a total of 1680
geometrical elements. The split: 1680 = 780 + 900 matches (apart from the
tetractys/Tree of Life factor of 10) the number values of the Hebrew words “cholem” and
“Yesodoth” making up the Mundane Chakra of Malkuth. Moreover, there are 1680 turns in
each helical whorl of the basic unit of matter described by Besant & Leadbeater
over a century ago and now identified as the E8×E8 heterotic
superstring! This extraordinary embodiment of the superstring structural parameter 1680
in the geometry of the disdyakis triacontahedron is very strong evidence that it is the
cosmic blueprint defining both the dynamics and structure of superstrings. Further
confirmation that this is not a coincidence is the fact that there are 900 geometrical
elements in the polyhedron down to the equator and 780 elements below it. The two words
“Yesodoth” and “cholem” define the numbers of geometrical elements making up,
respectively, half the polyhedron and the remainder of it.
16
Number values of Yesodoth (90) & Cholem (78) define the numbers of geometrical
elements
in the disdyakis triacontahedron to, respectively, its
equator and below its equator.
17
|
Figure 9
The gematria number value 168 of Cholem Yesodoth
is the number of yods other than corners associated with each set of the first six
enfolded polygons making up the inner Tree of Life. The pentagon, hexagon & octagon
have 90 yods and therefore embody the number value of Yesodoth. The triangle,
square & decagon have 78 yods, so that they embody the number value of
Cholem. The polyhedral counterpart of this is the triakis tetrahedron. When
the interior triangles formed by its centre and edges are each divided into three
sectors, there are 90 vertices & triangles surrounding an axis passing through two
opposite vertices and 78 edges. As the Catalan solid with the fewest number of edges
(see the table on p. 9 in Part 2 of Article 40), it is the only semi-regular polyhedron
with this property. The Catalan solid with the largest number of edges is the disdyakis
triacontahedron. Similarly constructed, it has 900 vertices & triangles and 780
edges surrounding an axis joining two opposite vertices, that is, exactly ten
times the corresponding numbers for the triakis tetrahedron. It is as if the disdyakis
triacontahedron is the tetractys of the world of polyhedra and the triakis tetrahedron
is one of its ten yods.
This hidden, ten-fold nature of the disdyakis triacontahedron is
confirmed by the fact that, associated with the 60 polygons of the first six types
enfolded in ten overlapping Trees of Life are 900 yods other than corners in
the ten pentagons, ten hexagons and ten octagons and 780 yods other than corners in the
ten triangles, ten squares & ten decagons (“associated” means that only one of the
two hexagonal yods in each shared, root edge is included in the count, the other
hexagonal yod being associated with the other set of polygons).
18
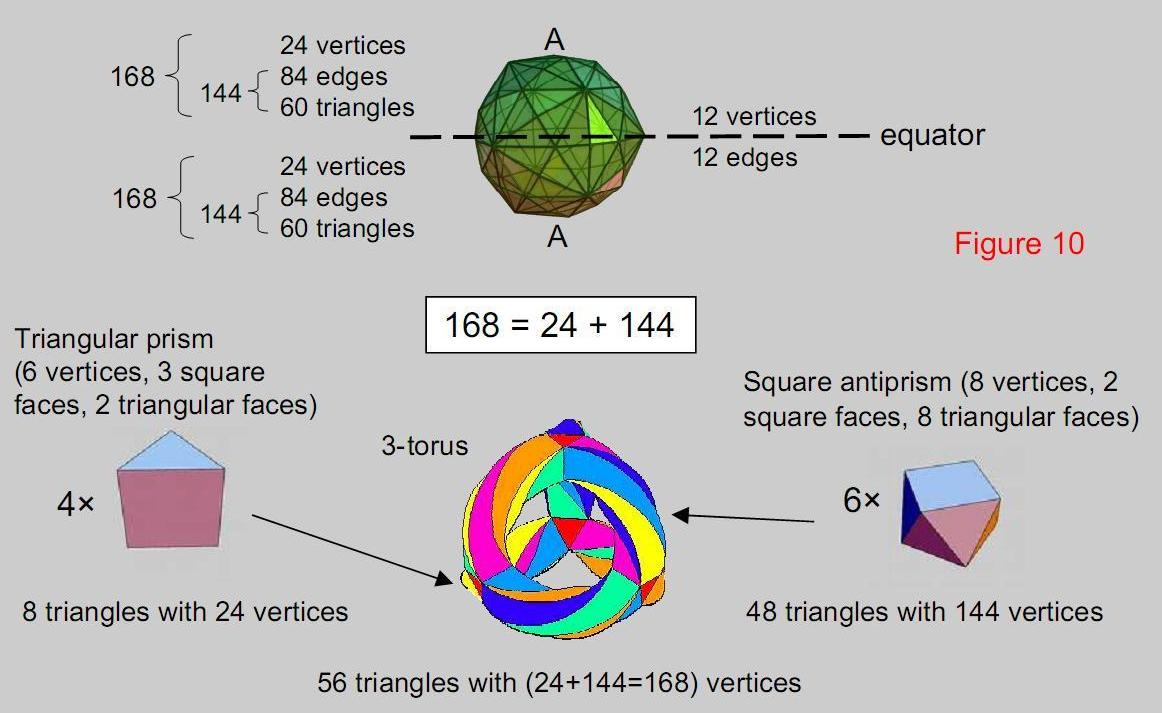
Figure 10
Above or below the equator of the disdyakis triacontahedron between
two opposite vertices are 168 geometrical elements. They comprise 4 edges & 60
triangles, i.e., 144 elements, and 24 vertices. This 24:144 division of the geometrical
parameter 168 is found in the {3,7} mapping onto a 3-torus of the 168 automorphisms of
the Klein quartic, as now explained: the 3-torus is topologically equivalent to a
tetrahedral array of four triangular prisms to whose 12 square faces is attached the 12
square faces of six antiprisms (see pp. 12 & 13 of Part 3 of Article 40) The four triangular prisms
have eight triangles with 24 vertices; the six square antiprisms have 48 triangles
with 144 vertices. So 56 triangles with (24+144=168) vertices tile the 3-torus. The
24 vertices of the triangular prisms correspond to the 24 vertices above or below
the equator of the disdyakis triacontahedron. The 144 vertices of the square
antiprisms correspond to the 144 edges & triangles above or below the equator.
The two halves of the polyhedron outside the equator correspond to the 3-torus
mapping the 168 automorphisms of the Klein quartic and its turned inside-out
version, which maps its 168 anti-automorphisms.
This correlation is further evidence that the disdyakis
triacontahedron embodies the symmetry of SL(2,7) displayed by the Klein quartic.
20
Isomorphism between the (24+144) geometrical elements of
the disdyakis triacontahedron above & below the
equator and the (24+144) vertices of the (8+48) triangles
tiling the 3-torus and its turned inside-out
form
21
|
Figure 11
The same 24:144 division is displayed by the yods in the set of the
first six enfolded polygons of the inner Tree of Life. The 168 yods other than corners
associated with each set includes 24 that belong to the pentagon. So each of these 24
yods symbolize a vertex of the eight triangles in the four triangular prisms joining
the six square antiprisms, whilst the 144 yods in the five other polygons denote the
144 vertices of the 48 triangles in the square antiprisms. As these vertices denote
automorphisms of PSL(2,7), one of which is the identity element, it is tempting to
identify the single hexagonal yod in the root edge that is associated with one set of
polygons as the identity I and the other hexagonal yod associated with the other set as
-I. The two identical sets of six polygons, each with 168 yods other than corners,
correspond to the {3,7} tiling of the 3-torus by 56 triangles with 168 vertices mapping
the 168 automorphisms and by the 56 triangles on its turned inside-out version mapping
the 168 anti-automorphisms. Every yod in the six enfolded polygons that is not one of
its corners symbolizes a symmetry of the Klein quartic. The two mirror-image sets of
polygons correspond to the 3-torus and to a 3-torus turned inside out.
22
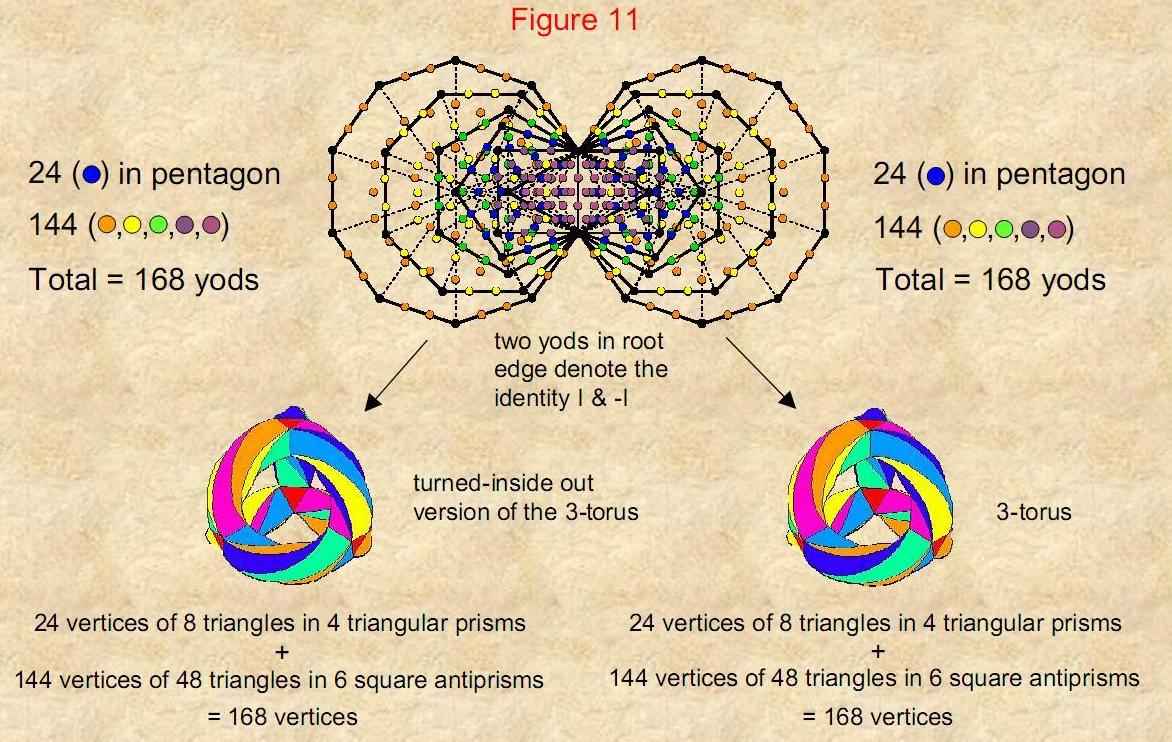
Each of the two sets of the first 6 enfolded polygons
of the inner Tree of Life has (24+144) yods. One
set is isomorphic to the (24+144) vertices of
the 56 triangles in the {3,7} tiling on a 3-torus of the 168
automorphisms of the
Klein quartic. The other mirror-image set is isomorphic to the
(24+144) vertices
of the 56
triangles on the turned inside-out 3-torus tiling the 168
anti-automorphisms.
23
|
Figure 12
As further confirmation of the remarkable isomorphism between the
inner Tree of Life, the disdyakis triacontahedron and the tiling of the 168 symmetries
of the Klein quartic onto a 3-torus, the same 24:144 division of the
respective yods, geometrical elements and vertices of triangles is exhibited in the
boundaries of the two sets of the first six polygons. 168 yods lie on their edges
outside their shared root edge. Of these, 24 red yods are corners of the pair of
hexagons and decagons outside their shared root edge. 144 black yods lie on the 60
external edges of the other eight polygons. The Godname EL of Chesed with number value
31 prescribes the first six enfolded polygons because they have 31 sides. The Godname
YAH with number value 15 prescribes the enfolded hexagon and decagon with 15 edges.
24
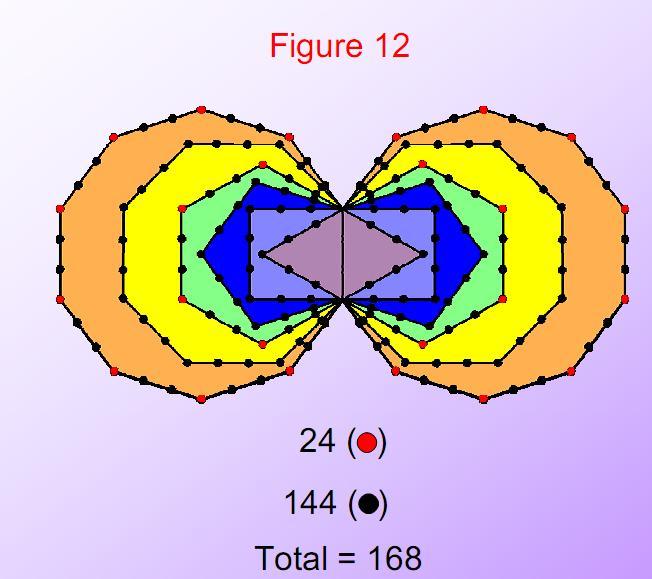
The pair of 24:144 divisions of: 1.
geometrical elements in the disdyakis triacontahedron, 2. yods in
the first (6+6) regular polygons of the inner Tree of Life and 3.
triangles in the {3,7} tiling of the 168 automorphisms and the 168
antiautomorphisms of the Klein quartic on a 3-torus is a
fundamental property of holistic systems. This basic division
appears not only in each set of 6 enfolded polygons but also in the
pair of them. There are 24 corners of the two hexagons and
the two decagons outside the shared root edge and 144 yods on the
external edges of the two sets of polygons. In other words, 168
yods are needed to delineate their shapes, confirming the
character of this number as a structural parameter of the heterotic
superstring as the microscopic manifestation of the Tree of Life
blueprint.
25
|
Figure 13
Each of the ten closed curves of the basic unit of matter described
by Annie Besant and C.W. Leadbeater is a helix with 1680 turns. As each curve winds
five times around the spin axis of the particle, it makes 336 helical turns in one
revolution, that is, 168 turns in a half-revolution. This 168:168 division corresponds
to:
-
the (168+168) geometrical elements in the faces of the disdyakis
triacontahedron above and below its equator;
-
to the 168 automorphisms and 168 anti-automorphisms of the Klein quartic as
represented by the 168 vertices of the 56 triangles tiled on the 3-torus and
the 168 vertices of the 56 triangles tiled on its turned inside-out
version;
-
the (168+168) yods other than corners in the first (6+6) enfolded
polygons;
-
the (168+168) lines/broken lines in the 56 off-diagonal hexagrams of the I
Ching table.
26
Figure 14
When the 47 sectors of the seven enfolded polygons are transformed
into 2nd-order tetractyses (the next order above the tetractys in which yods are
replaced by tetractyses), they contain 3360 yods. This is the number of helical turns
made by all ten closed curves of the E8×E8' heterotic superstring
when they make one revolution around the spin axis of the spin-½ particle. Each yod
denotes a turn. Physically, it is an oscillation of the circularly polarized standing
wave running around the curve. The Godname ELOHIM with number value 50 prescribes the
fundamental constituent of quarks because its ten whorls make 50 revolutions about its
spin axis. Assigning this number to each of the yods in the inner Tree of Life
generates the number 16800 as the number of circularly polarized oscillations in the
ten closed curves of the heterotic superstring.
28
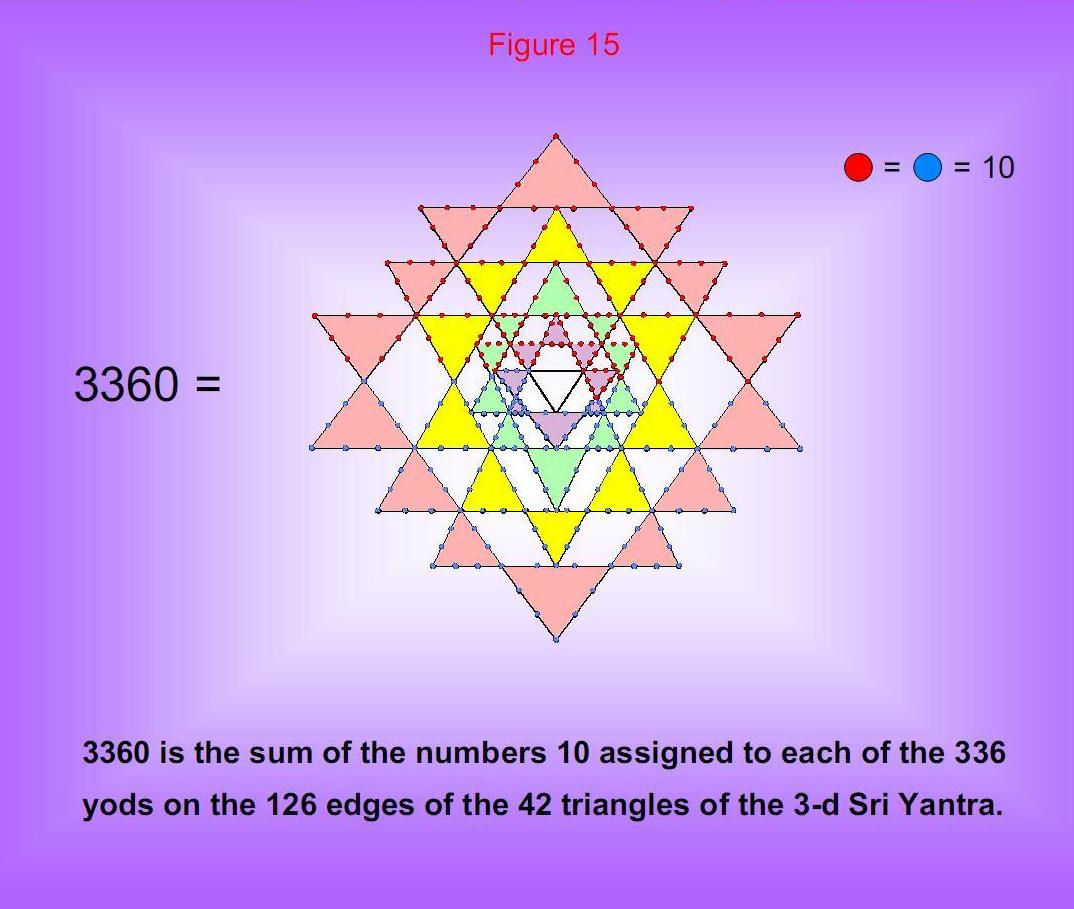
Figure 15
Assigning the number 10 (the Pythagorean Decad) to the 336 yods on
the 126 edges of the 42 triangles of the 3-dimensional Sri Yantra generates the number
3360. This demonstrates how the Sri Yantra and the inner Tree of Life are equivalent
representations of holistic systems like the heterotic superstring. Each half of the
Sri Yantra with 168 yods defines the number (1680) of circularly polarized oscillations
made by all ten closed curves of the superstring during half of a revolution around its
spin axis. The inner and outer halves of the superstring correspond to the two halves
of the Sri Yantra. They are prescribed by the Godname EHYEH with number value 21
because each half is made of 21 triangles.
30
|
31
|
Figure 16
The Godname of Malkuth is ADONAI. Its number value is 65. It
prescribes the lowest ten overlapping Trees of Life because they have 65 Sephiroth.
When their triangles are each constructed from three tetractyses, there are 1680 yods
below the top of the tenth tree – the 65th Sephirah. Each yod symbolizes a circularly
polarized oscillation in each closed curve of the heterotic superstring. It shows how
ADONAI, the Godname of the Sephirah signifying the physical universe, prescribes the
form of the basic unit of matter.
There are 1680 yods outside the shared edges that lie on the edges
of the first six polygons enfolded in each of ten overlapping Trees of Life on either
side of the central Pillar of Equilibrium. This demonstrates the shape-defining
character of this structural parameter of the E8×E8' heterotic
superstring.
32
Figure 17
Suppose that the 50 faces of the five Platonic solids are
constructed from tetractyses. The four faces of the tetrahedron have 48 hexagonal yods,
the eight faces of the octahedron have 96 hexagonal yods, the six faces of the cube
have 96 hexagonal yods, the 20 faces of the icosahedron have 240 hexagonal yods and the
12 faces of the dodecahedron have 240 hexagonal yods.
34
Figure 18
The 62 vertices of the disdyakis triacontahedron generate 10
tetrahedra, five octahedra, five cubes, one icosahedron, one dodecahedron, five rhombic
dodecahedra and one rhombic triacontahedron. The 28 polyhedra contain 3360 hexagonal
yods when their faces are constructed from tetractyses. The superstring structural
parameter 3360 is embodied in the polyhedral potential of the disdyakis
triacontahedron, demonstrating its remarkable archetypal character. Notice that the
four Platonic solids representing the four elements of Earth, Water, Air and Fire have
1680 hexagonal yods. They comprise 1440 hexagonal yods in the solids representing Fire,
Air & Earth and 240 hexagonal yods in the icosahedron representing Water. The same
240:1440 division is exhibited in the other seven polyhedra. It is another
manifestation of the division discussed on pages 20-25 in the contexts of the disdyakis
triacontahedron, the tiling on the 3-torus of the 168 symmetries of the Klein quartic
and the yods in the first six enfolded polygons.
36
|

3360 hexagonal yods are needed to
construct from tetractyses the 28 regular and
semiregular
polyhedra generated by the vertices of
the disdyakis triacontahedron
37
|
Figure 19
A Hypothesis
Hypothesize that each of the three generations of basic fermions has
seven colour states, one defining leptons and six defining subquarks. Each generation
consists of two weak isospin states, each isospin state consists of two supersymmetric
states, each supersymmetric state is a particle and its antimatter counterpart and each
particle exists in left-hand and right-hand parity states. This implies that there are
336 different particles made up of 168 left-handed states and 168 right-handed states.
This would correspond to the 168 geometrical elements in each half of the disdyakis
triacontahedron between opposite vertices and the equator. The inversion symmetry of
the polyhedron would naturally correspond to the distinction between left-handed
particles and their mirror image right-handed counterparts. Moreover, the 24
left-handed leptons would correspond to the 24 vertices above the equator, the 24
right-handed leptons would correspond to the 24 vertices below the equator and the 144
edges & triangles in each half of the polyhedron would correspond to the 144
left-handed and 144 right-handed subquarks. The 24 triangles in each of the seven
segments of the {7,3} tiling of the Klein quartic would signify the 24 left-handed or
right-handed particles in each of the seven colour states.
As we have seen (pp. 20-25), the inner Tree of Life, the I Ching
table, the Sri Yantra and the disdyakis triacontahedron also embody the number 168 and
its division into 24 and 144. The physical meaning of this would be that the former is
the number of leptons of a given handedness (3×2×2×2) and that the latter is the number
of subquarks of the same handedness (3×6×2×2×2). Do, therefore, the 168 automorphisms
and 168 anti- automorphisms of the Klein quartic have a physical interpretation in
terms of these states of matter fields? Is the field of order 7 in PSL(2,7) the seven
colour states?
38
Figure 20
It requires seven colours to colour a map drawn on a 2-torus.
K7, the complete graph of order 7, can be embedded on a 2-torus. This is the
topology of each whorl of the unit of matter described by Besant & Leadbeater. The
seven vertices of K7 could symbolize the seven colour states of each generation
of superstring, the 21 straight lines joining its vertices corresponding to the 21 colour
states of the three generations of superstrings. Turning the straight lines into
bi-directional arrows generates (7+7=14) arrows pointing along the edges of the graph and
(14+14=28) arrows pointing inwards, that is, 42 arrows. This correlates with the 42
triangles of the Sri Yantra, the 14 arrows corresponding to the 14 triangles in the fourth
layer and the 28 arrows corresponding to the 28 triangles in the first three layers. It
would seem that the correlation, if not accidental, means that the Sri Yantra is defining
the seven-fold nature of holistic systems, e.g., the musical intervals above the tonic, the
seven musical scales, the seven unit imaginary octonions and the seven colour states of
superstrings.
40
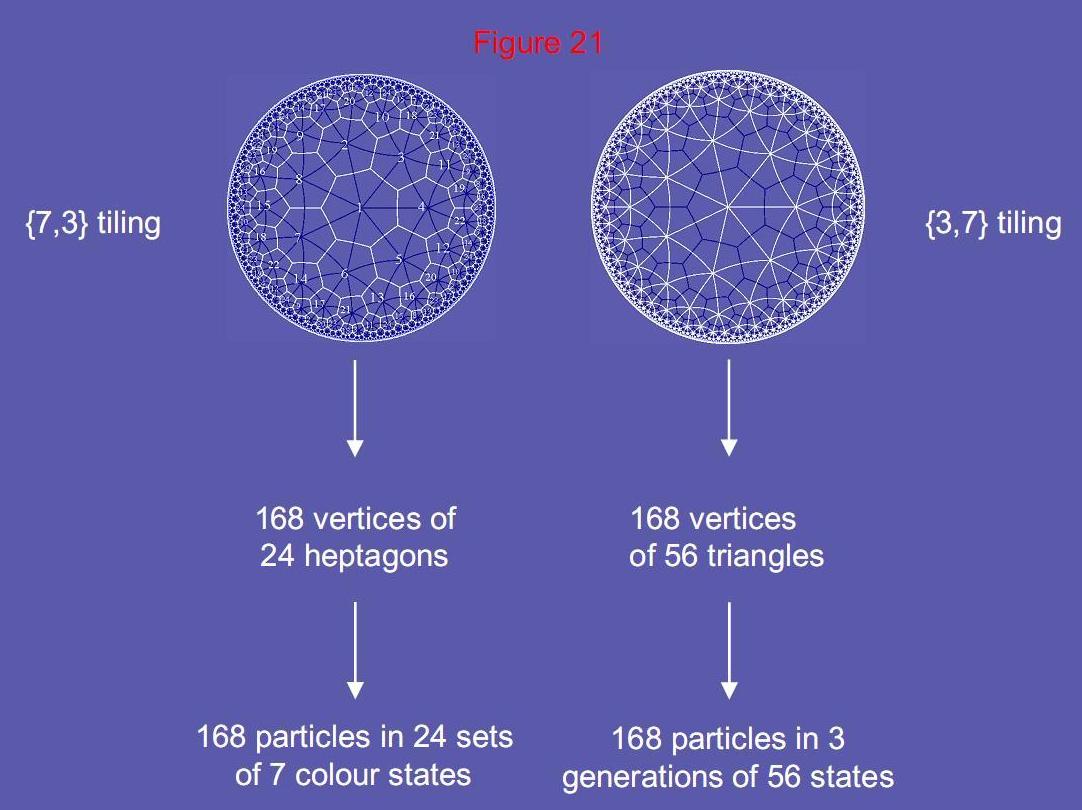
Figure 21
The 168 vertices of the 24 heptagons in the {7,3} mapping of the 168
automorphisms of the Klein quartic may denote the 168 particles in 24 sets of seven
colour states. The 168 vertices of the 56 triangles in the {3,7} mapping of the 168
automorphisms may denote the 168 particles made up of three generations of 56
states.
42
|
A physical
interpretation of the Klein configuration.
43
|
Figure 22
The first six enfolded polygons have 26 corners. One corner on the root
edge is associated with one set of polygons and the other corner is associated with the
other set. The topmost corner of the hexagon coincides with the lowest corner of the
hexagon enfolded in the next higher tree. This means that the 42 polygons enfolded on each
side of seven overlapping Trees of Life have 168 corners associated with them that are
truly intrinsic to them because none belong to the polygons enfolded in the next higher
tree. The number of independent degrees of freedom represented by these corners is
therefore (168+168=336). They correspond in the {7,3} hyperbolic mapping of the 168
automorphisms and 168 anti-automorphisms of the Klein quartic to, respectively, the 168 red
hyperbolic triangles and the 168 blue hyperbolic triangles. The counterpart of the 24
triangles in each of the seven segments of the Klein configuration is the set of 24 corners
associated with each set of polygons. In each case, the 24 degrees of freedom may denote
the 24 particles in each of the seven colour states. If this true, then the seven colour
states are the manifestation of the seven Sephiroth of Construction. The colour state
defining leptons would correspond to Malkuth and the six colour states defining subquarks
would correspond to the two triads of Sephiroth of Construction above Malkuth.
44
|
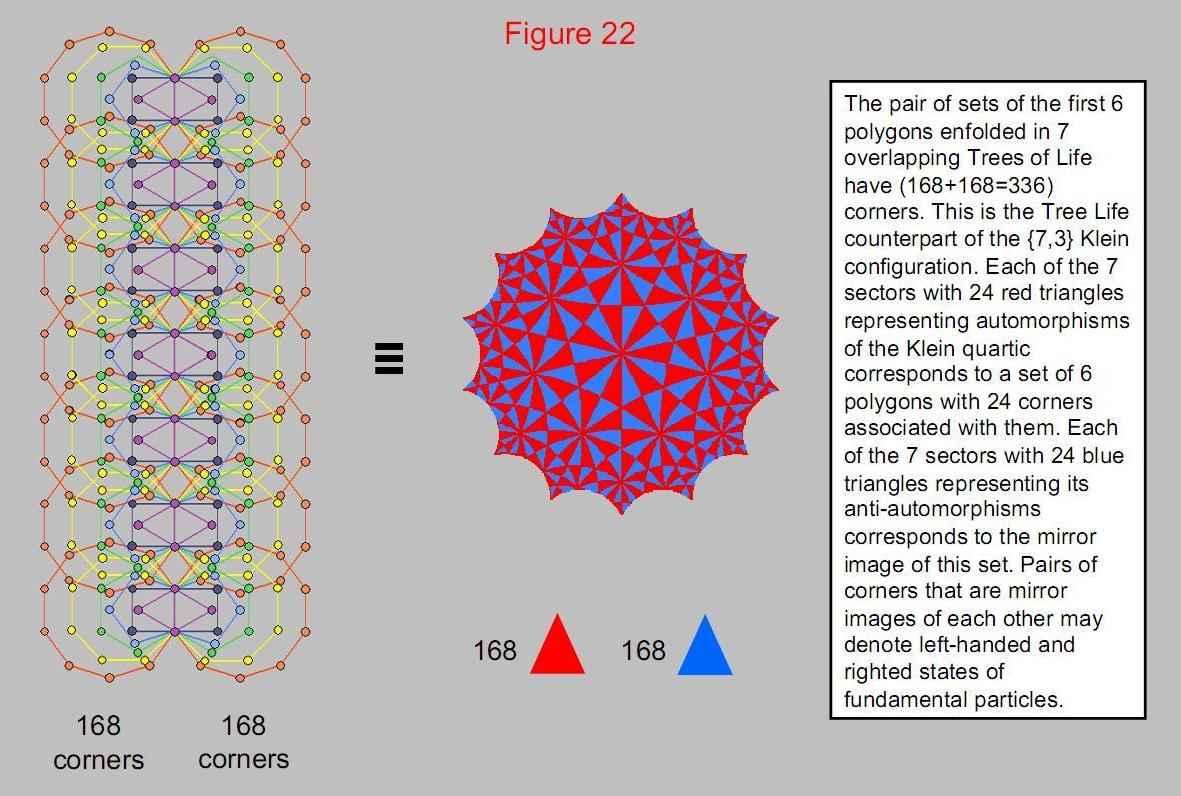
The Tree of Life counterpart of the Klein
configuration.
45
|
|
Figure 23
Earlier, we found that the I Ching table is isomorphic to the {3,7}
mapping of the 168 automorphisms of the Klein quartic. The 56 trigrams of the 28
off-diagonal hexagrams in one half of the table correspond to the 56 hyperbolic
triangles whose 168 vertices represent automorphisms. Just as there are 56 sets of
three rows of lines/broken lines, so there are 56 particle states in each of three
generations. The three rows of a trigram define the three possible generations of
superstrings. The eight different trigrams denote the (23=8) states for each
colour: weak isospin doublet(2)×supersymmetric doubling(2)×particle/antiparticle(2).
The 168 lines and broken lines in the 28 hexagrams in one half of the table denote
left-handed, superstring matter fields. The 168 lines and broken lines in the 28
hexagrams in the other half of the table denote right-handed particles.
Amongst the 90 intervals below the octave between the 14 types of
notes found in the seven musical scales, there are 24 pairs of intervals and their
complements. Three pairs of intervals are intervals between notes belonging to two
different musical scales. They are not notes of these scales. This leaves 21 pairs of
intervals that are notes of the seven scales. They correspond to the 21 basic, colour
states of the three generations of superstrings and their antimatter, supersymmetric or
weak isospin-doublet partners.
46
Figure 24
The 24:168 division that, as we have seen, is displayed by various
sacred geometries appears in the sequence of tone ratios of the notes of the
Pythagorean scale. The perfect fifth of the fifth octave has the tone ratio 24. It is
the tenth overtone and the 33rd note in the sequence. Indeed, every 33rd note increases
in pitch by a factor of 24 and becomes the tenth overtone relative to the starting
note. There are 24 overtones up to the note with tone ratio 192. So 14 overtones span a
tone ratio difference of 168 between the note with tone ratio 24 and that with tone
ratio 192. The notes of the seven musical scales have 189 intervals below the octave.
They include 21 notes that are the second, third and fourth notes of each scale,
leaving 168 intervals. Including the tonic, the octave and the unit interval between a
note and itself, there are 192 intervals. They comprise 24 intervals (tonic, octave,
unit interval and the 21 notes) and 168 intervals made up of the 21 complements of the
21 notes and 147 intervals between notes above the tonic (21 in each scale). Both the
seven musical scales and the Pythagorean scale display the 24:168 division found for
the inner Tree of Life, the I Ching table and the Sri Yantra.
48
|
Figure 24
Tone ratios of the notes in the Pythagorean
musical scale
|
|
C
|
D
|
E
|
F
|
G
|
A
|
B
|
Number
of overtones
|
|
1
|
1
|
9/8
|
81/64
|
4/3
|
3/2
|
27/16
|
243/128
|
0
|
|
2
|
2
|
9/4
|
81/32
|
8/3
|
3
|
27/8
|
243/64
|
2
|
|
3
|
4
|
9/2
|
81/16
|
16/3
|
6
|
27/4
|
243/32
|
4
|
|
4
|
8
|
9
|
81/8
|
32/3
|
12
|
27/2
|
243/16
|
7
|
|
5
|
16
|
18
|
81/4
|
64/3
|
24
|
27
|
243/8
|
11
|
|
6
|
32
|
36
|
81/2
|
128/3
|
48
|
54
|
243/4
|
15
|
|
7
|
64
|
72
|
81
|
256/3
|
96
|
108
|
243/2
|
20
|
|
8
|
128
|
144
|
162
|
512/3
|
192
|
216
|
243
|
26
|
Note G of the eighth octave (its perfect 5th) has
the tone ratio 192. It is the 24th overtone. Note G of the fifth octave
has the tone ratio 24. It is the tenth overtone. So 14 overtones span a
tone ratio difference of 168 between the 24th overtone and the tenth
overtone. Including the tonic, octave and unit interval common to the
seven musical scales, there are 192 intervals between the notes of the
seven scales. They comprise 24 intervals (tonic, octave, unit interval
and the 2nd, 3rd & 4th notes of each scale) and 168 intervals. We
have seen how the number 192 has appeared in various sacred geometries
as a measure of a holistic system. For example, there are 192 yods
associated with the first six enfolded polygons, of which 24 yods are
their corners. There are 192 lines/broken lines in each half of the I
Ching table, of which 24 lines/broken lines make up the eight basic
trigrams, leaving 168 lines/broken lines in the 28 hexagrams above or
below the diagonal. There are 192 yods in each half of the Sri Yantra
(including the central triangle). They comprise the three hexagonal
yods on the edges of the central triangle, the centres of the 21
triangles and the 168 yods on the edges of these triangles, i.e., they
divided into a set of 24 yods and a set of 168 yods. Finally, there are
192 geometrical elements surrounding the centres of the seven separate,
regular polygons. They comprise the 24 elements surrounding the centre
of the hexagon and the 168 elements surrounding the centres of the
other six polygons. The intervals between the notes of the seven
musical scales have the same 24:168 division, demonstrating that they
are elements of a holistic system.
49
|
Figure 25
42 triangles of the Sri Yantra surround the central one. Suppose
that their 126 sectors are each constructed from three triangles that are then turned
into tetractyses. Each triangle is composed of 46 yods. It comprises seven vertices, 15
edges and nine triangles, i.e., 31 geometrical elements, showing how the Godname EL of
Chesed with number value 31 prescribes the most elementary shape when constructed from
tetractyses. The value 1 of the Hebrew letter aleph (E) denotes the vertex at the
centre of the triangle and the value 30 of the Hebrew letter lamed (L) denotes the 30
geometrical elements that surround it. As the nine triangles making up each triangle of
the Sri Yantra have 15 edges, the Godname YAH of Chokmah with number value 15
prescribes these structural units, whilst the Godname EHYEH of Kether with number 21
prescribes them because there are 21 vertices and edges surrounding the centre of a
triangle. 36 yods lying on edges of the nine tetractyses surround the centre, where 36
is the number value of ELOHA, Godname of Geburah. This is also the extra number of yods
that have to be added to change the triangle from a tetractys with ten yods into one
with 46 yods. Each triangle has 39 hexagonal yods and one centre (shown as black yods).
There are (42×40=1680) of these yods in the Sri Yantra. Alternatively, there are 1680
yods other than outward tips of triangles and interior corners of triangles. They
symbolize the 1680 helical turns in each closed curved of the heterotic superstring. As
a geometrical paradigm of wholeness, the Sri Yantra represents the form of the basic
unit of matter.
50
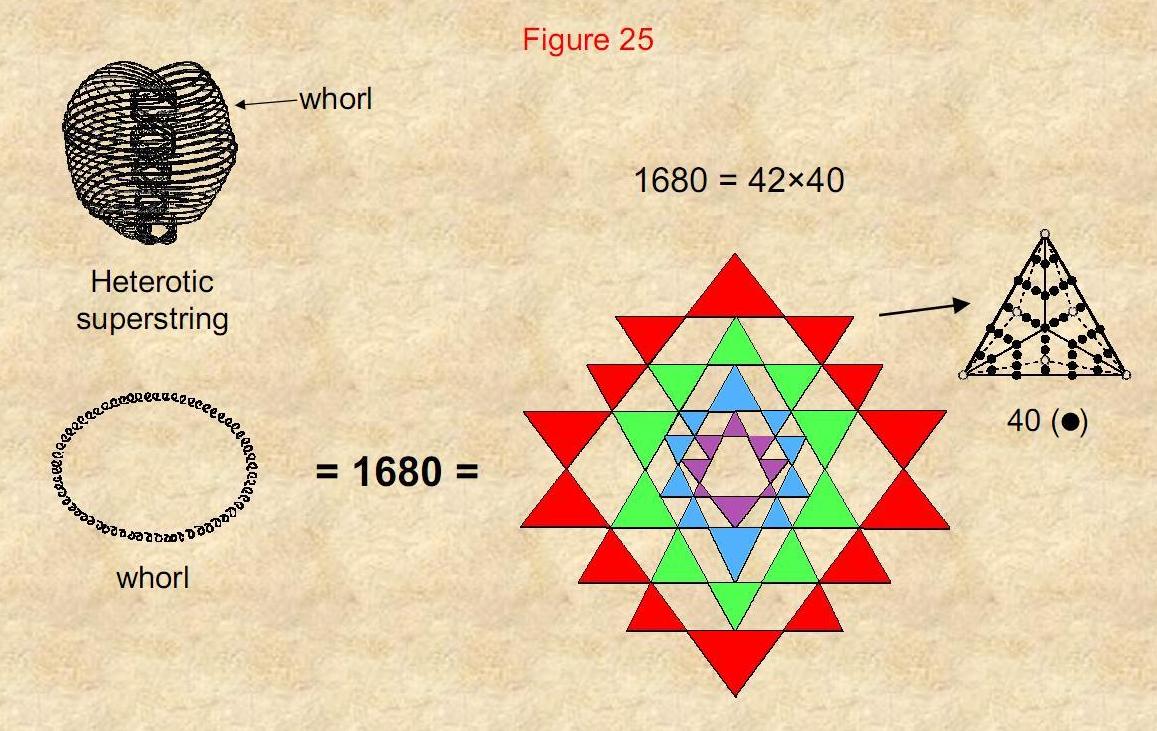
The 1680 ( )
yods in the 42 triangles of the Sri Yantra symbolize )
yods in the 42 triangles of the Sri Yantra symbolize
the 1680 turns in each helical whorl of the
heterotic superstring.
51
|
|