Abstract
|
No doubt because of their fear of peer ridicule, mathematicians have taken little professional interest in the ‘sacred geometries’ of various cultures and mystical traditions. It may, therefore, surprise them to learn that Leibniz, the great German mathematician and philosopher who discovered calculus at the same time as Sir Isaac Newton, chose to analyze the table of hexagrams used in Chinese divination and found that it was a binary number representation of the vertices of a cube and the lines that join them. He did not pursue the matter further, and apart from studies by a few architects and mystically minded geometers, little cross-cultural study of sacred geometries like the Kabbalistic Tree of Life and the Tantric Sri Yantra have been made with the aim of elucidating what (if any) is the nature of the information hidden in these purported blueprints for all existence. Academics are loath to examine such a topic partly because of the far-reaching (indeed, paradigm-shifting) implications that they would have to confront if they ever found significant, but rationally unexplainable, similarities between purported representations of God’s design for His universe, even though these geometrical systems are separated in provenance by thousands of miles and years! This article reveals mostly in pictorial form what the archetypal nature of these sacred geometries is and what they imply for particle physics (for more details, refer to Articles 19-39 on the author’s website). The latter has to be tentative as yet because this material summarizes work still in progress. The former, however, can be established with the rigour of a proof of a theorem of Euclidean geometry and does not require model-dependent interpretation. The present purpose is not to discuss the implications – religious and philosophical – of a demonstration that certain sacred geometries are isomorphic to one another. Rather, it is to assemble and then to compare research results from other articles by the author so as to identify the essential properties shared in different ways by the sacred geometries of the Tree of Life, the I Ching & the Sri Yantra. This research article will prove conclusively that the fundamental information that they contain relates to the superstring nature of matter. In his various books, the author proved beyond reasonable doubt that superstrings were described over 100 years ago with the aid of a yogic siddhi called ‘anima.’ This mental faculty generates highly magnified images of microscopic objects as they exist in real time, i.e., they are NOT merely symbolic. The information embodied in the sacred geometries discussed here relate unequivocally to the details of this description of the basic constituents of matter. However amazing it may be, such a conclusion should come as no surprise, given that these geometries are isomorphic blueprints that determine the very nature of reality, including physical matter. A supersymmetric generalization of the Standard Model used by particle physicists will be hypothesized in order to interpret the common characteristics of these geometries. Previous articles by the author have shown that their properties also appear in the Catalan solid called the ‘disdyakis triacontahedron,’ which was found to be the polyhedral counterpart of both the Tree of Life and the Sri Yantra. Like them, this polyhedron possesses amazing properties that are unique to itself. However, it also shares with them equally amazing features that indicate that the essential meaning of its spectacular geometry is identical to theirs, as, indeed, it has to be because they are ALL expressions of the one universal blueprint. Despite differences in morphology, their essential similarity can only be regarded as irrefutable evidence of a universal archetype pervading the sacred geometries of East and West that can now be shown to manifest in the mathematics of music. Moreover, it is one that is beginning to appear in the research journals of particle physics. This is the true ‘theory of everything,’ for the blueprint in sacred geometries applies not only to matter but to ALL holistic systems. |
2
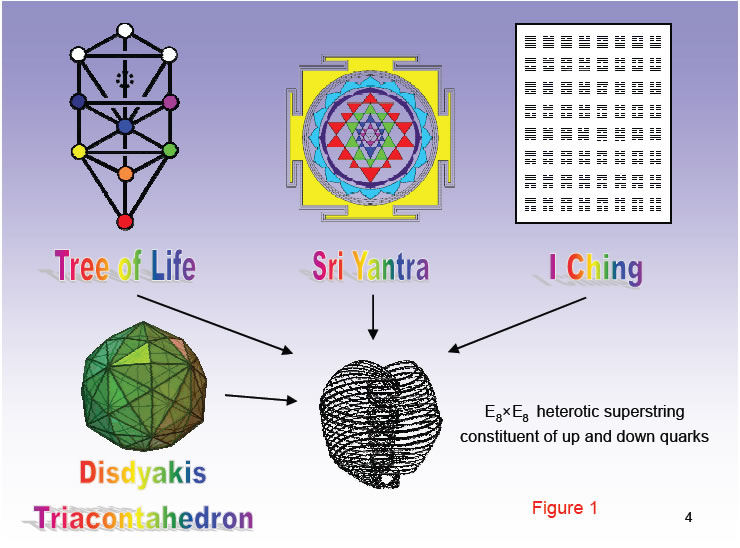
At the heart of Kabbalah, the Jewish mystical tradition, is the glyph called the Tree of Life (Otz Chiim). It is a geometrical representation of Adam Kadmon (Heavenly Man), the divine paradigm forming the basis of all holistic systems.
The Sri Yantra is the most famous and revered of the yantras used in India for meditation. So old that its origin is unknown, it depicts the nature of Creation.
The I Ching table has been used for hundreds of years in China for the purpose of divination. Its 64 hexagrams consist of pairs of trigrams, each a set of three parallel lines that are either Yang (unbroken) or Yin (broken).
The disdyakis triacontahedron is the most complex of the Catalan solids– generated from the Archimedean solids by interchanging vertices and faces.
Over a century ago, the leading Theosophists, Annie Besant and C.W. Leadbeater, claimed to observe the subatomic unit of matter with a yogic siddhi . The author has proved that this object is the E8×E8' heterotic superstring constituent of up and down quarks.
Article 40 shows that the Tree of Life, the Sri Yantra, the I Ching table and the disdyakis triacontahedron embody the same universal blueprint as that which manifests in the smallest subatomic particle.3
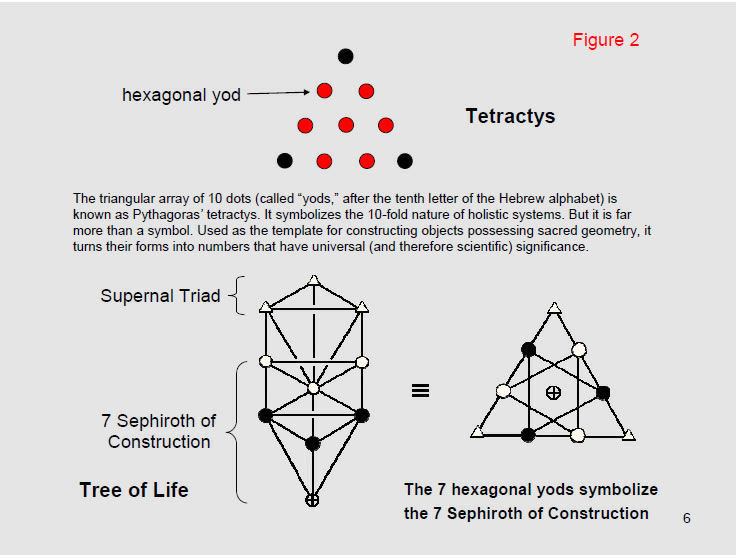
The tetractys is at the core of the mathematical philosophy of Pythagoras. A symbol of holistic systems, it is equivalent to the Kabbalistic Tree of Life. Each of its ten yods symbolizes one of the ten Sephiroth of the Tree of Life. The three yods at its corners symbolize the Supernal Triad (the triple Godhead). The seven hexagonal yods at its centre or at the corners of a hexagon denote the seven Sephiroth of Construction.
5
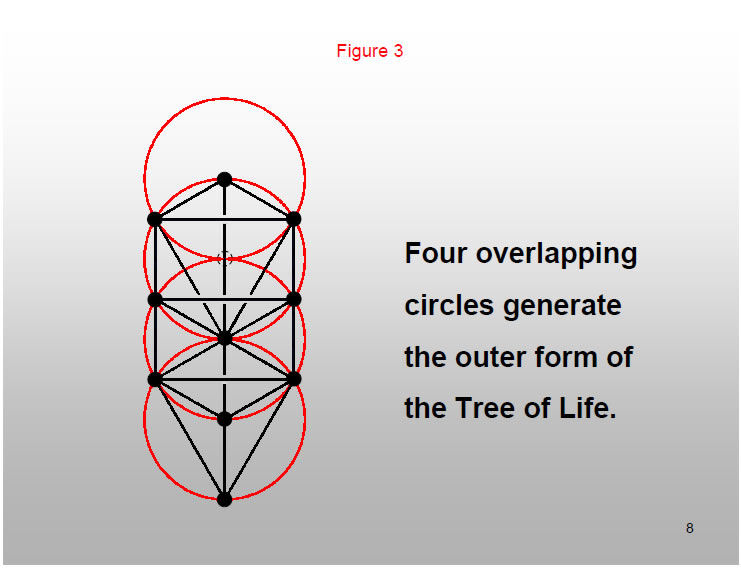
Four circles arranged in a vertical line and overlapping centre-to-circumference generate the positions of the ten Sephiroth of the Tree of Life.
7
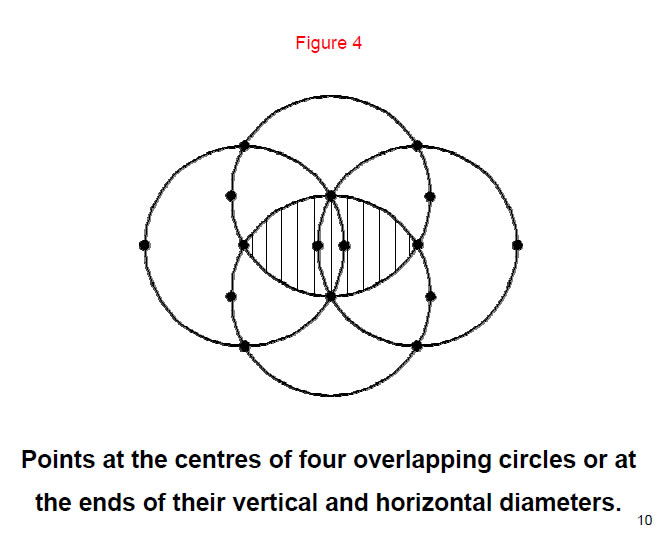
Two similar, overlapping circles form a Vesica Piscis (shown shaded) as their region of overlap. Its apices are the centres of two new circles. The four circles have 18 centres and endpoints of their vertical and horizontal diameters. The 16 points shown are sufficient to generate the “inner” form of the Tree of Life.
9
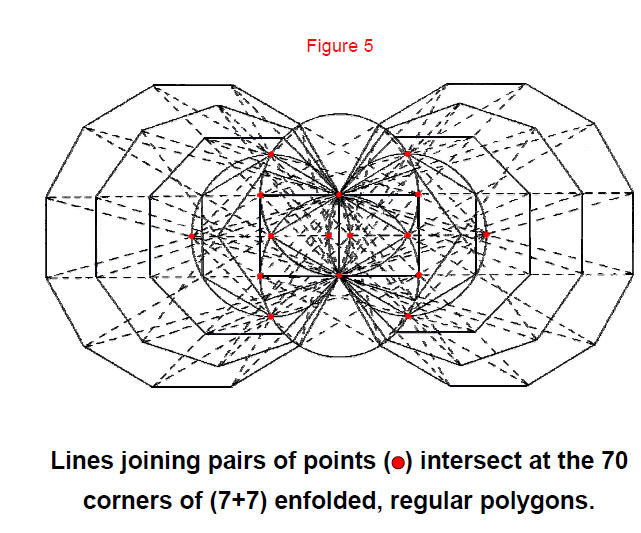
The inner form of the Tree of Life is generated from its outer form by joining pairs of points that belong to the set of 16 points. Straight lines joining pairs of points intersect at the 70 corners of two similar sets of seven regular polygons enfolded in one another and sharing one edge (the “root edge”).
11
12
The 3-dimensional, outer Tree of Life can be projected onto the plane of the two sets of enfolded polygons that constitute its inner form. Six of their corners outside their shared edge are shared with Sephiroth of the Tree of Life. Their corners on the root edge coincide with Tiphareth and with Daath. The outer and inner forms of the Tree of Life have 73 corners, where 73 is the number value of Chokmah (“Wisdom”), the second Sephirah.
13
14
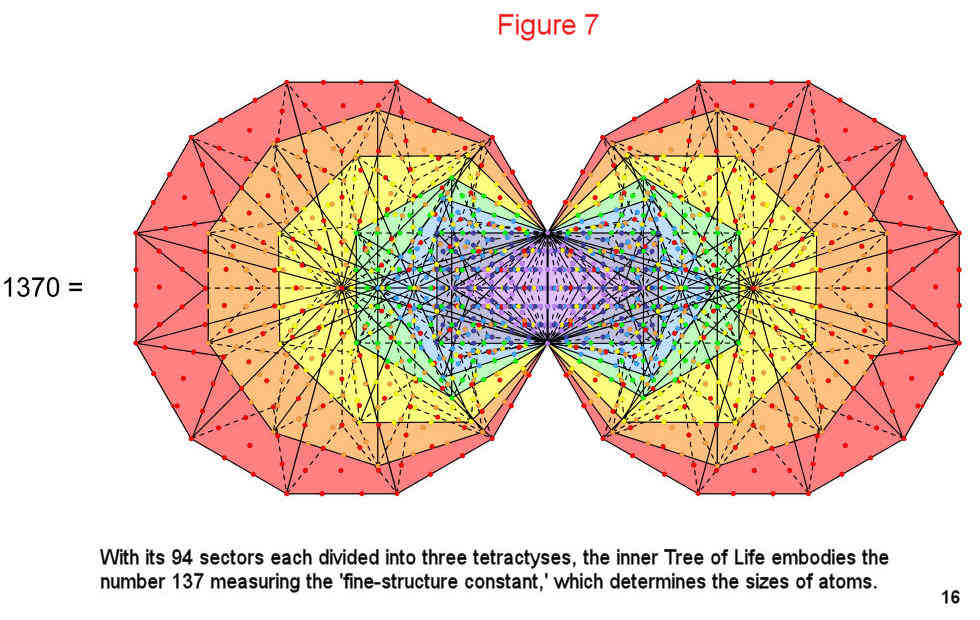
The number 137 is embodied in the blueprint of the inner Tree of Life. Its (7+7) enfolded polygons have 94 sectors. When they are each divided into three tetractyses, 1370 yods are generated, that is, the number of yods in 137 tetractyses. This proves beyond question that the number 137 is a basic structural parameter of the Tree of Life, in keeping with its central status in physics as a number which determines one of the fundamental constants of nature – the so-called 'fine-structure constant,' whose magnitude sets the scale of the energies of electrons in atoms.
15
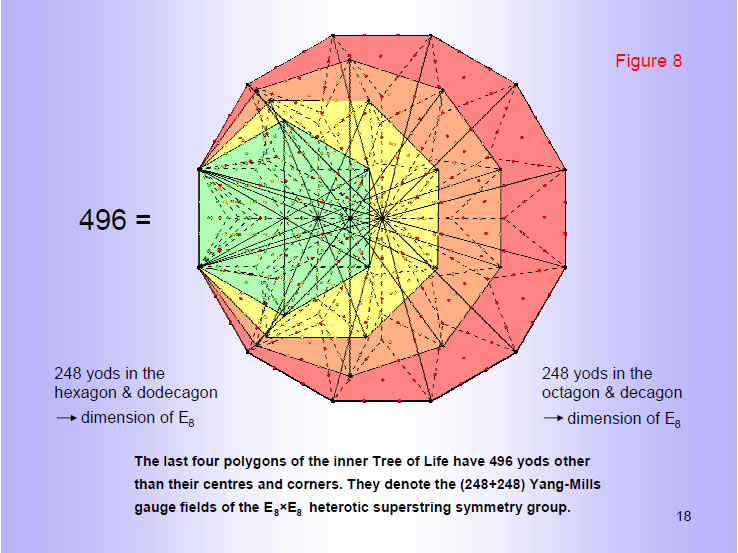
496 extra yods are needed to turn into three tetractyses each sector of the last four enfolded polygons of the inner Tree of Life. 248 yods belonging to the hexagon and dodecagon symbolize the 248 particles transmitting the superstring force with the symmetry of the gauge symmetry group E8 and 248 yods belonging to the octagon and decagon symbolize the 248 particles associated with E8' (identical to E8). The remarkable, natural division of the yod populations of the four polygons into two sets of 248 shows how the universal blueprint of the inner Tree of Life embodies the dynamics of the E8×E8' heterotic superstring. It also illustrates how the Pythagorean Tetrad (4) defines parameters of scientific significance, for it is the last four regular polygons that embody the number 496 characterizing the unified force between superstrings.
17
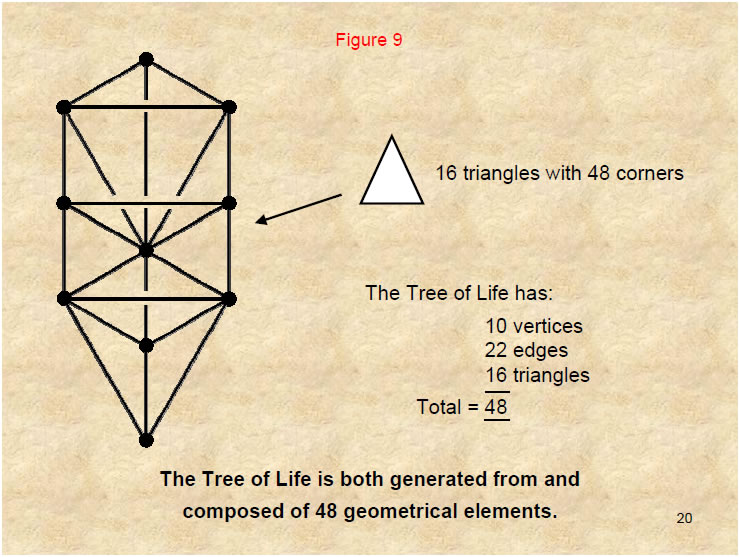
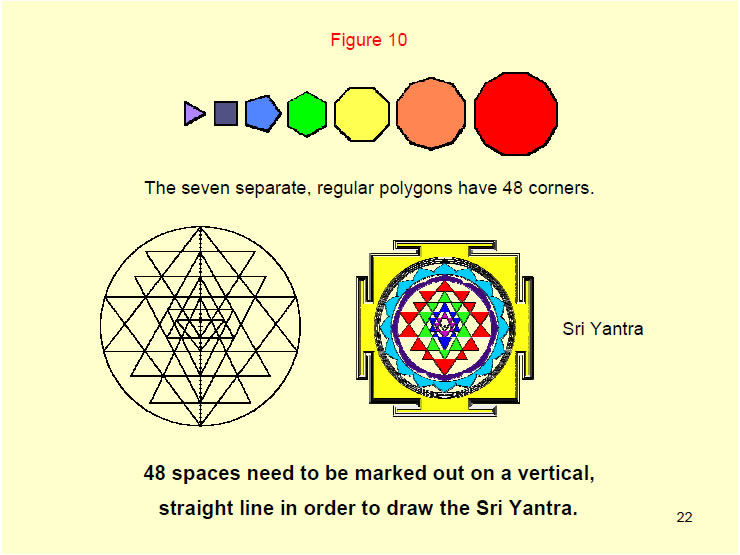
16 separate triangles with 48 corners join together to form the Tree of Life. It has 10 vertices and 22 edges of 16 triangles – a total of 48 geometrical elements. The re-appearance of this number is not a coincidence because it is a basic parameter of all geometrical structures that conform to the archetypal Tree of Life pattern and possess sacred geometry. 48 is the number value of Kokab, the Mundane Chakra of Hod.
19
The number 48 also characterises the inner form of the Tree of Life. It is a set of seven enfolded polygons which, when separate, have 48 corners.
The Sri Yantra is difficult to draw accurately because a slight error at any stage of its construction can seriously distort the diagram. A template that achieves this task is a vertical, straight line with 48 spaces of the same width marked out on it.
21
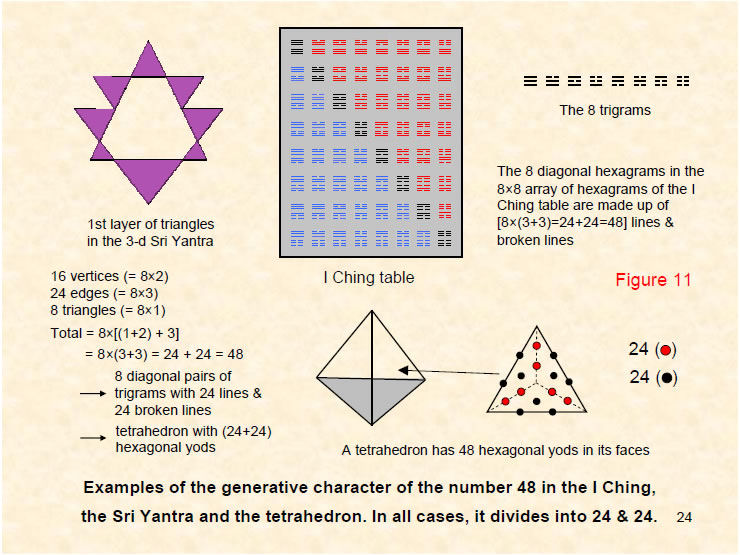
The parameter 48 characterising sacred geometry is displayed in the Sri Yantra, the I Ching table and the tetrahedron. The first layer of triangles in the Sri Yantra consists of eight triangles joined corner to corner. They have 16 vertices, 24 edges and eight triangles, totally 48 geometrical elements as two sets of 24. The eight hexagrams (shown black) along the diagonal of the I Ching table have 48 unbroken and broken lines as two sets of 24. The tetrahedron – the simplest Platonic solid – has four faces. When each face is divided into its three sectors and the latter then turned into tetractyses, there are 48 hexagonal yods in the 12 tetractyses. They comprise 24 red hexagonal yods inside each face and 24 black hexagonal yods on the edges of the tetrahedron. This division into two sets of 24 of the 48 degrees of freedom embodied in the generative, or germinal aspect of a holistic system is characteristic of such systems.
23
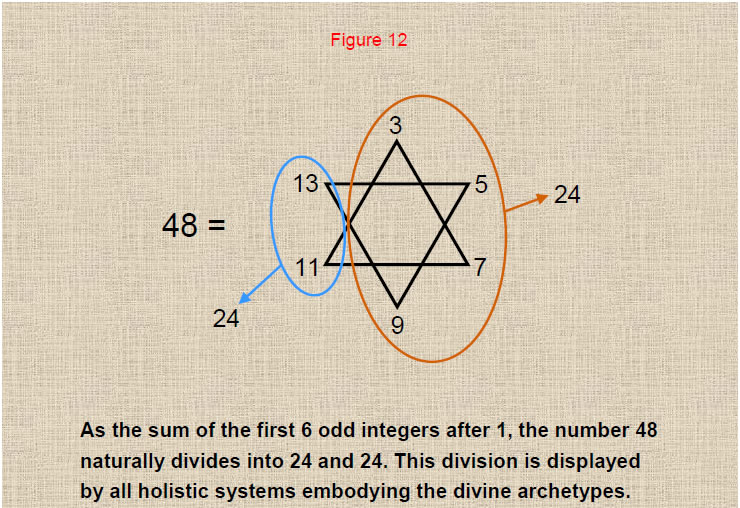
The number 48 is the sum of the first six odd integers after 1. 24 is the sum of the first four odd integers after 1. Arithmetically, therefore, the number 48 divides naturally into a pair of number 24s. The encircled selections are the only ones that add up to 24. As we shall see, this division always appears in holistic systems that display sacred geometry.
25
26
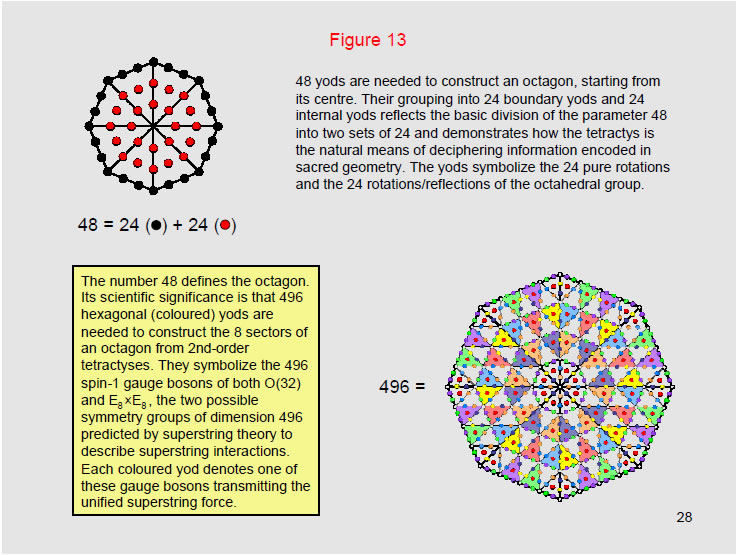
The octagon constructed from tetractyses displays the same 24:24 division of the 48 yods surrounding its centre. There are 24 yods on its boundary and 24 inside it surrounding its centre.
When constructed from “2nd-order” tetractyses, in which each yod of a tetractys is replaced by a tetractys, the octagon has 496 hexagonal yods. They symbolize the 496 spin-1 particles that superstring theory predicts transmit the unified superstring force. Surrounding the centre of the octagon are 80 corners of tetractyses. 80 is the number value of Yesod, the penultimate Sephirah of the Tree of Life. 496 is the number value of Malkuth, the final Sephirah.
27
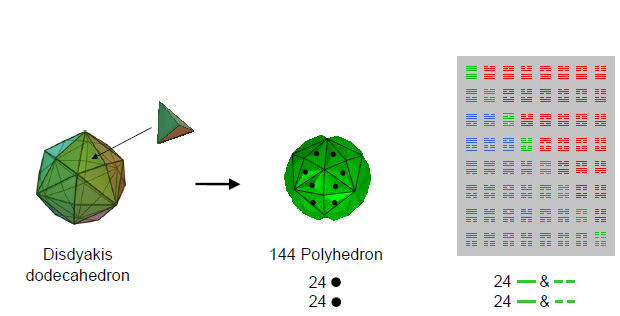
The holistic parameter 48 exists in the 144 Polyhedron (see Article 23 for details), the polyhedron which – together with the disdyakis triacontahedron – constitutes the polyhedral version of, respectively, the inner and outer forms of the Tree of Life. It is generated by attaching tetrahedra to the 48 faces of the disdyakis dodecahedron, which has 26 vertices and 72 edges. The latter is generated from the rhombic dodecahedron by sticking rhombic pyramids onto its 12 faces. The resulting 48 faces comprise 24 faces and their 24 mirror images. This means that the 48 peaks of the tetrahedra consist of 24 vertices and their 24 mirror images. This is how the 144 Polyhedron displays the 24:24 division of the parameter 48. Their counterpart in the I Ching table are the 24 lines & broken lines in the eight upper and eight lower trigrams making up the eight diagonal hexagrams. Each half of a disdyakis dodecahedron consists of six sets of four faces, i.e., four sets of six faces. The grouping of the 48 faces into eight sets of six means that 48 of the (48+26=74) vertices of the 144 Polyhedron are similarly grouped. They correspond to the eight diagonal hexagrams of the I Ching table, each with six lines/broken lines, and to the eight sets of geometrical elements making up the eight triangles in the first layer of the Sri Yantra. They are related to the 24 rotational symmetries and the 24 rotation/reflection symmetries of the octahedral group.
29
Attaching tetrahedra to the 48 faces of the disdyakis dodecahedron with 26 vertices generates the 144 Polyhedron with (48+26=74) vertices. The 8 groups of 6 peaks of these tetrahedra are the counterparts of the 8 diagonal hexagrams of the I Ching diagram, each with 6 lines/broken lines. The 24 peaks in each half of the 144 Polyhedron correspond to the 24 lines/broken lines in one set of 8 trigrams and their Yang/Yin opposites in the other set making up the 8 diagonal hexagrams. They signify the (24+24=48) symmetries of the octahedral group.
30
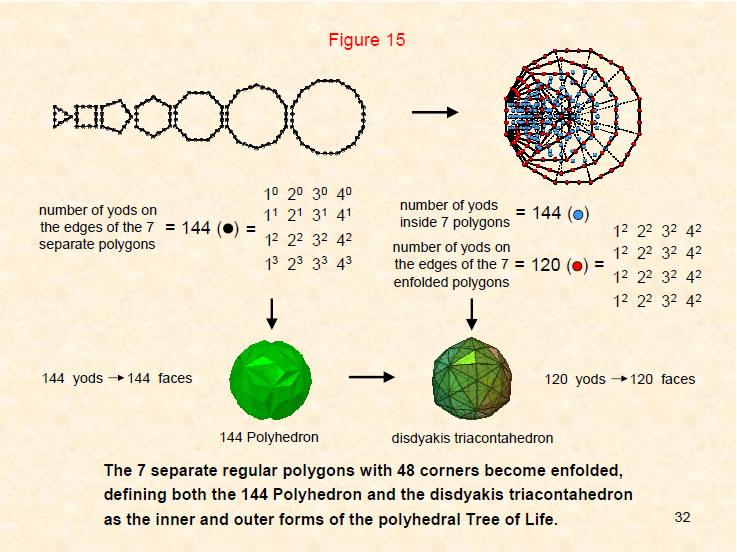
The correspondence between the polygonal and polyhedral versions of the Tree of Life is revealed here. As the generator of the disdyakis triacontahedron, the 144 Polyhedron has 144 faces creating its shape. This is the number of yods needed to create the 48 form-generating edges of the seven separate, regular polygons of the inner Tree of Life when the sectors of the latter are turned into tetractyses. It is also the number of yods inside the seven enfolded polygons and surrounding their centres. This corresponds to the 144 Polyhedron being the inner form of the polyhedral Tree of Life. It should therefore be thought of as inside the disdyakis triacontahedron — the outer form of the polyhedral Tree of Life. Just as there are 120 faces shaping the latter, so there are 120 yods on the 42 edges of the seven enfolded polygons that delineate their shapes. The polyhedral version of the outer and inner Trees of Life displays the same 144:120 division as their polygonal counterpart. This is because they are both isomorphic representations of holistic systems.
The Pythagorean Tetrad (4) defines the numbers 120 and 144 as square arrays of powers of the integers 1, 2, 3 & 4 symbolized by the four rows of dots in the tetractys.
31
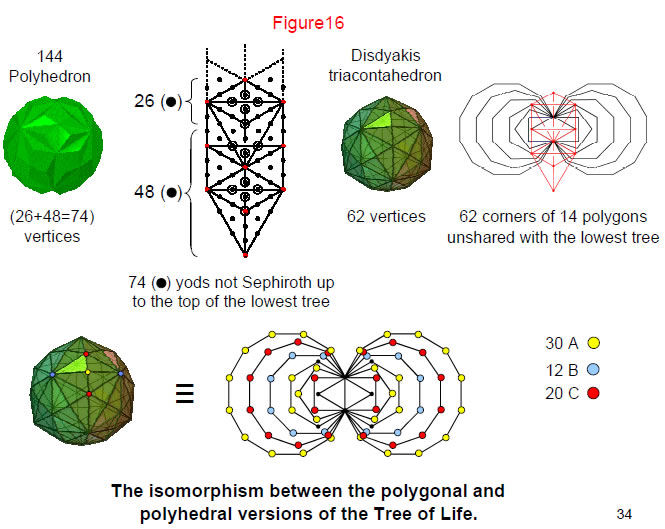
There are 84 yods up to the level of the lowest Tree of Life when it is constructed from tetractyses. Of these, ten are Sephiroth, leaving 74 yods other than Sephiroth. This is the number of non-Sephirothic degrees of freedom hidden within the outermost form of the Tree of Life. They comprises 26 yods down to the level of Daath and 48 yods below it. These yods correspond, respectively, to the 26 vertices of the disdyakis dodecahedron underlying the 144 Polyhedron and to the 48 vertices of the tetrahedra attached to its 48 faces.
The inner form of the lowest Tree of Life is two similar sets of seven enfolded polygons with 70 corners. They share seven corners with Sephiroth of the Tree of Life and one corner with Daath (both denoted by black yods), leaving 62 corners. These 62 independent degrees of freedom correspond to the 62 vertices of the disdyakis triacontahedron. The 31 corners of each set of polygons are the counterpart of the 31 vertices of this polyhedron and their mirror images. The 30 corners of the two sets of pentagons, hexagons & dodecagons correspond to the 30 A vertices, the 12 corners of the two octagons correspond to the 12 C vertices (vertices of an icosahedron). The 20 corners of the square & decagon correspond to the 20 A vertices (vertices of a dodecahedron).
The 144 Polyhedron and the disdyakis triacontahedron are therefore implicit in the geometry of the outer and inner forms of the Tree of Life as their polyhedral counterparts.
33
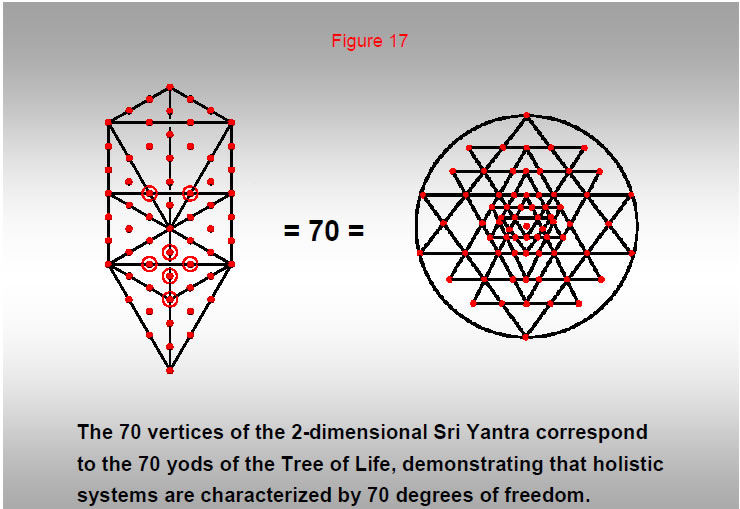
Turned into tetractyses, the 16 triangles of the Tree of Life have 70 yods. This is the number of vertices (including the central bindu point) of the 2-dimensional Sri Yantra. This demonstrates the isomorphism between these representations of holistic systems.
35
36
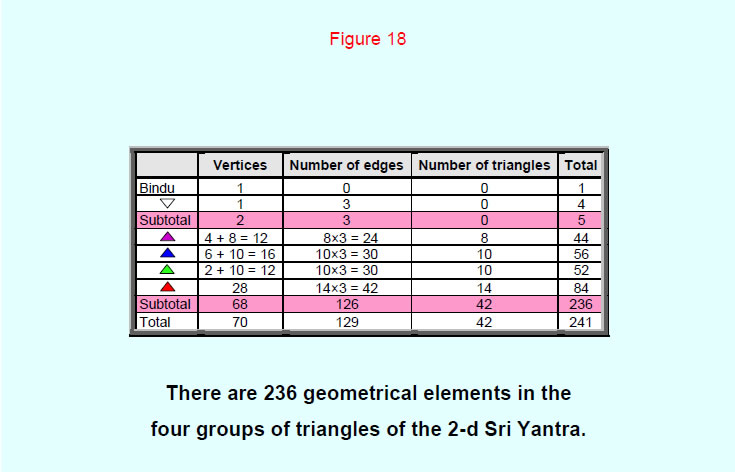
The four groups of triangles in the 2-dimensional Sri Yantra are composed of 236 geometrical elements. (The central triangle does not count formally as a triangle because of the bindu, or point, at its centre).
37
38
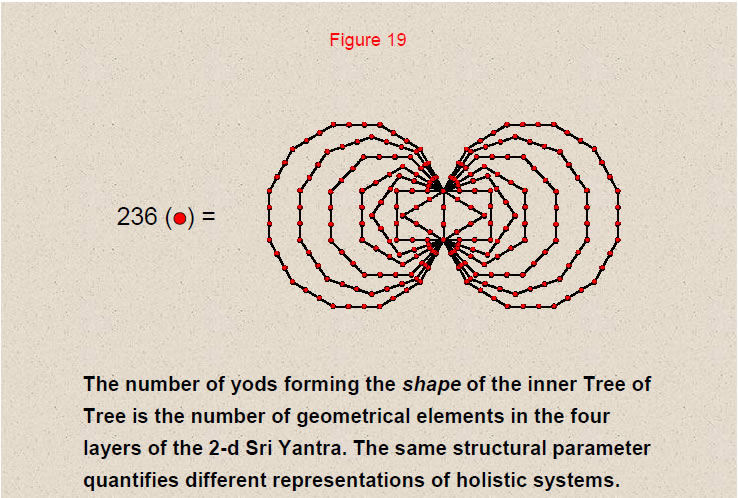
236 yods lie on the 83 edges of the two identical sets of seven enfolded polygons constituting the inner Tree of Life. This the number of geometrical elements that compose the 42 triangles of the 2-dimensional Sri Yantra. Different representations of holistic systems embody the same structural parameter.
39
40